文档内容
领取更多免费资料关注微信公众号:网盘网课资源
决胜 2024 年高考数学押题预测卷 05
数 学
(新高考九省联考题型)
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己
的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.某地有8个快递收件点,在某天接收到的快递个数分别为360,284,290,300,188,240,260,
288,则这组数据的百分位数为75的快递个数为( )
A. 290 B. 295 C. 300 D. 330
2.已知复数 满足 ,则 ( )
A. B. C. D. 1
3. 若 ,则 ( )
A. B. C. D.
4.已知 , ,m为实数,若 ,则向量 在 上的投影向量为( )
A. B. C. D.
5.已知圆 ,弦 过定点 ,则弦长 不可能的取值是( )
A. B. C. 4 D.
6.若 ,x, ,则 的最小值为( )
A. B. C. D. 4
7.在 中,角 所对的边分别为 , ,若 表示
的面积,则 的最大值为( )
A. B. C. D.
8.已知 ,使 恒成立的有
序数对 有( )
A. 2个 B. 4个 C. 6个 D. 8个
1领取更多免费资料关注微信公众号:网盘网课资源
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若 ,则( )
A. B. C. D.
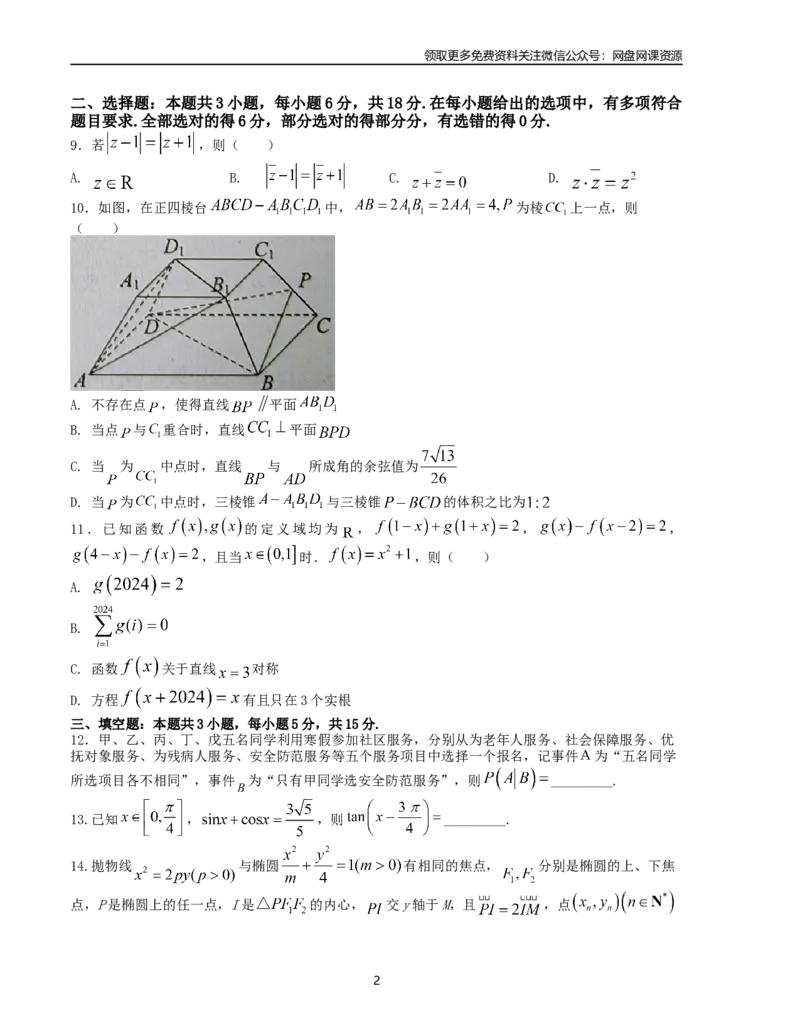
10.如图,在正四棱台 中, 为棱 上一点,则
( )
A. 不存在点 ,使得直线 平面
B. 当点 与 重合时,直线 平面
C. 当 为 中点时,直线 与 所成角的余弦值为
D. 当 为 中点时,三棱锥 与三棱锥 的体积之比为
11.已知函数 的定义域均为 , , ,
,且当 时. ,则( )
A.
B.
C. 函数 关于直线 对称
D. 方程 有且只在3个实根
三、填空题:本题共3小题,每小题5分,共15分.
12.甲、乙、丙、丁、戊五名同学利用寒假参加社区服务,分别从为老年人服务、社会保障服务、优
抚对象服务、为残病人服务、安全防范服务等五个服务项目中选择一个报名,记事件 为“五名同学
所选项目各不相同”,事件 为“只有甲同学选安全防范服务”,则 _________.
13.已知 , ,则 _________.
14.抛物线 与椭圆 有相同的焦点, 分别是椭圆的上、下焦
点,P是椭圆上的任一点,I是 的内心, 交y轴于M,且 ,点
2领取更多免费资料关注微信公众号:网盘网课资源
是抛物线上在第一象限的点,且在该点处的切线与x轴的交点为 ,若 ,则
_______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
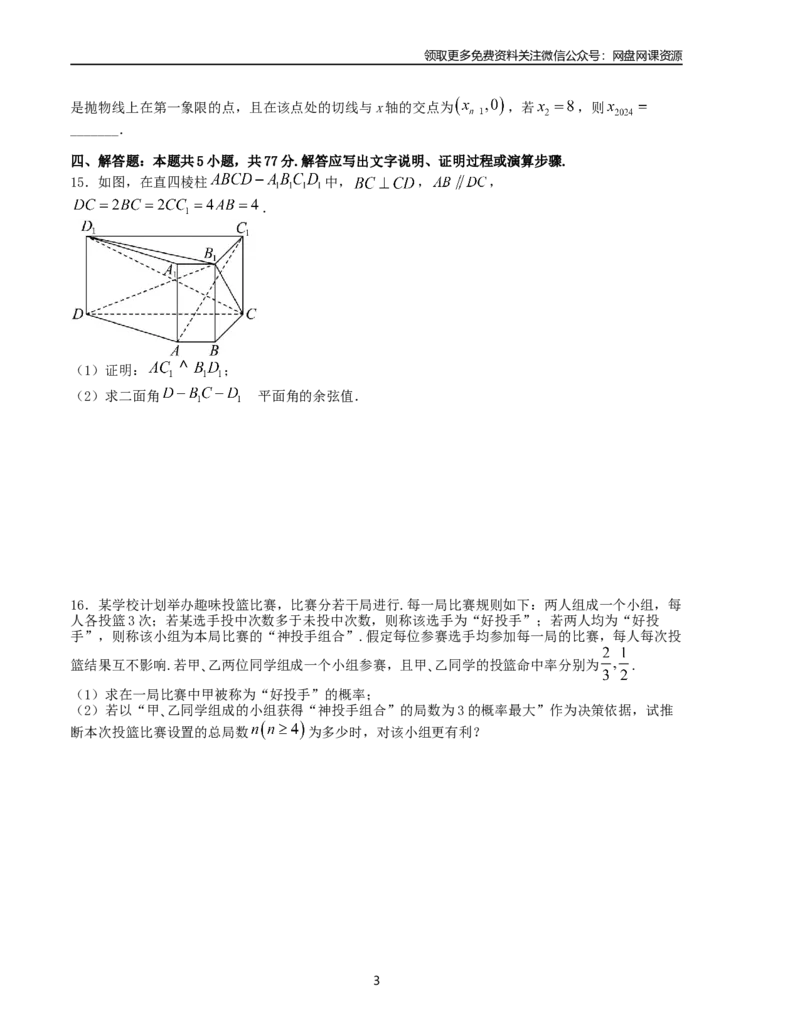
15.如图,在直四棱柱 中, , ,
.
(1)证明: ;
(2)求二面角 的平面角的余弦值.
16.某学校计划举办趣味投篮比赛,比赛分若干局进行.每一局比赛规则如下:两人组成一个小组,每
人各投篮3次;若某选手投中次数多于未投中次数,则称该选手为“好投手”;若两人均为“好投
手”,则称该小组为本局比赛的“神投手组合”.假定每位参赛选手均参加每一局的比赛,每人每次投
篮结果互不影响.若甲、乙两位同学组成一个小组参赛,且甲、乙同学的投篮命中率分别为 .
(1)求在一局比赛中甲被称为“好投手”的概率;
(2)若以“甲、乙同学组成的小组获得“神投手组合”的局数为3的概率最大”作为决策依据,试推
断本次投篮比赛设置的总局数 为多少时,对该小组更有利?
3领取更多免费资料关注微信公众号:网盘网课资源
17.设函数 ,其中a为实数.
(1)当 时,求 的单调区间;
(2)当 在定义域内有两个不同的极值点 时,证明: .
18.设动点 与定点 的距离和它到定直线 的距离之比等于 ,记点M的
轨迹为曲线C.
(1)求曲线C的方程;
(2)设 过点 的直线与C的右支相交于A,B两点, 是 内一点,且满足
,试判断点 是否在直线 上,并说明理由.
19.若无穷数列 的各项均为整数.且对于 , ,都存在 ,使得
,则称数列 满足性质P.
(1)判断下列数列是否满足性质P,并说明理由.
4领取更多免费资料关注微信公众号:网盘网课资源
① , ,2,3,…;
② , ,2,3,….
(2)若数列 满足性质P,且 ,求证:集合 为无限集;
(3)若周期数列 满足性质P,求数列 的通项公式.
5