文档内容
高一第二学期期末数学试卷
一、选择题(共10小题).
1. ( )
A. B. C. D.
【答案】A
【解析】
【分析】
由诱导公式可得 的值.
【详解】解: .
故选:A.
【点睛】本题主要考查诱导公式及特殊角的三角函数值,考查基本的概念与知识,属于基础题.
2. 已知复数 ,则 的共轭复数 等于( )
A. 0 B. C. D.
【答案】C
【解析】
【分析】
由共轭复数的概念可得答案.
【详解】解:由复数 ,则 的共轭复数 ;
故选:C.
【点睛】本题主要考查共轭复数的概念,属于基础题型.
3. 在 中, , , ,则 ( )A. B. C. D.
【答案】B
【解析】
【分析】
由余弦定理得推论可得 的值.
【详解】在 中,由题意知:
,
故选:B
【点睛】本题考查了余弦定理得推理,属于基础题.
4. 下列正确的命题的序号是( )
①平行于同一条直线的两条直线平行;
②平行于同一条直线的两个平面平行;
③垂直于同一个平面的两条直线平行;
④垂直于同一个平面的两个平面垂直.
A. ①② B. ②④ C. ②③ D. ①③
【答案】D
【解析】
【分析】
由公理4即可判断①,平行于同一条直线的两个平面平行或相交即可判断②,由线面垂直的性质定理即可
判断③,垂直于同一个平面的两个平面可能相交或平行即可判断④
【详解】对于①:由公理4可得平行于同一条直线的两条直线平行,故①正确;
对于②:平行于同一条直线的两个平面平行或相交,故②错误;
对于③:由线面垂直的性质定理可得,垂直于同一个平面的两条直线平行,故③正确;
对于④:垂直于同一个平面的两个平面可能相交或平行,比如正方体的相对的两个底面就与侧面垂直,但
它们平行,故④错误.
故选:D
【点睛】本题主要考查了线面、线线的位置关系,属于基础题.
5. 如图,在正方形 中, 是 边的中点,设 , ,则 ( )A. B. C. D.
【答案】A
【解析】
【分析】
利用平面向量的加法法则可得出 关于 、 的表达式.
【详解】因为在正方形 中, 是 的中点,
设 , ,则 .
故选:A.
【点睛】本题考查平面向量的基底表示,考查了平面向量加法法则的应用,考查计算能力,属于基础题.
6. 如图记录了某校高一年级6月第一周星期一至星期五参加乒乓球训练的学生人数.通过图中的数据计算这
五天参加乒乓球训练的学生的平均数和中位数后,教练发现图中星期五的数据有误,实际有21人参加训练.
则实际的平均数和中位数与由图中数据星期得到的平均数和中位数相比,下列描述正确的是( )
A. 平均数增加1,中位数没有变化
B. 平均数增加1,中位数有变化
C. 平均数增加5,中位数没有变化
D. 平均数增加5,中位数有变化
【答案】B【解析】
【分析】
先求出平均数应增加 ,再求出中位数有变化,即得解.
【详解】实际星期五的数据为21人,
比原来星期五的数据多了 人,
平均数应增加 .
原来从星期一至星期五的数据分别为20,26,16,22,16.按从小到大的顺序排列后,原来的中位数是
20,
实际从星期一至星期五的数据分别为20,26,16,22,21.按从小到大的顺序排列后,实际的中位数是21.
所以中位数有变化.
故选:B.
【点睛】本题主要考查平均数和中位数的计算,意在考查学生对这些知识的理解掌握水平.
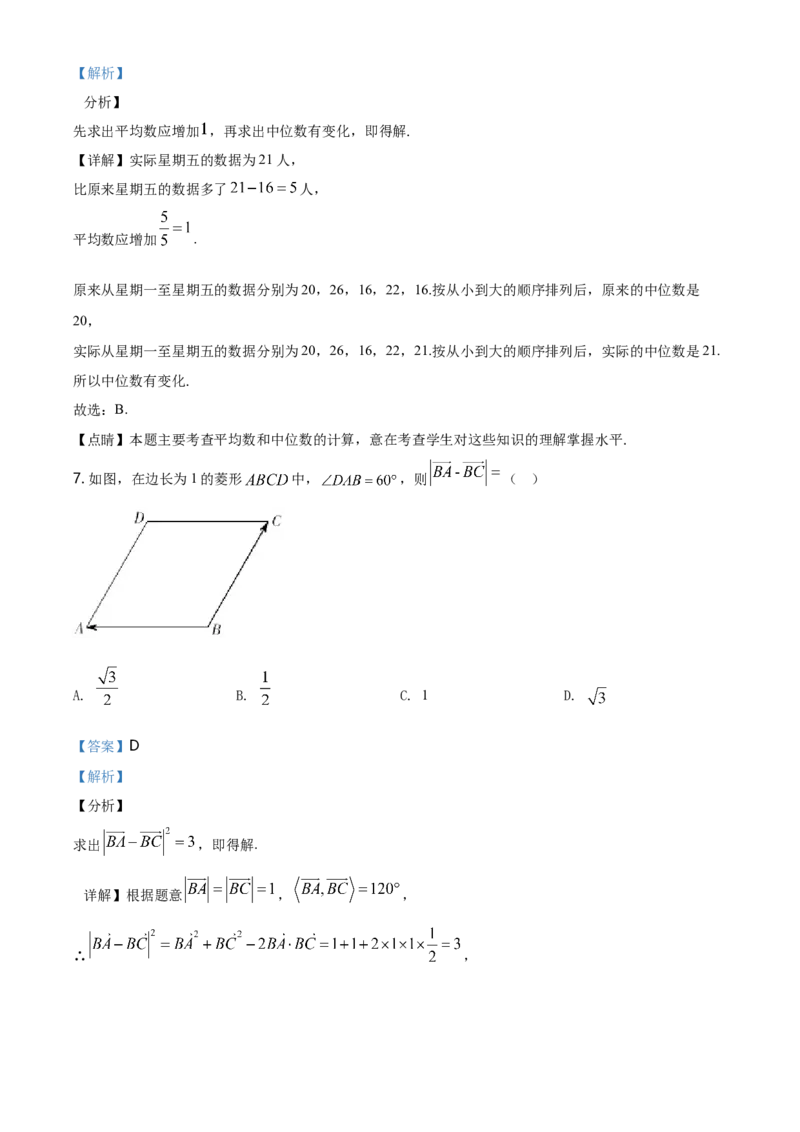
7. 如图,在边长为1的菱形 中, ,则 ( )
A. B. C. 1 D.
【答案】D
【解析】
【分析】
求出 ,即得解.
【详解】根据题意 , ,
∴ ,∴ .
故选:D.
【点睛】本题主要考查平面向量的模和数量积的计算,意在考查学生对这些知识的理解掌握水平.
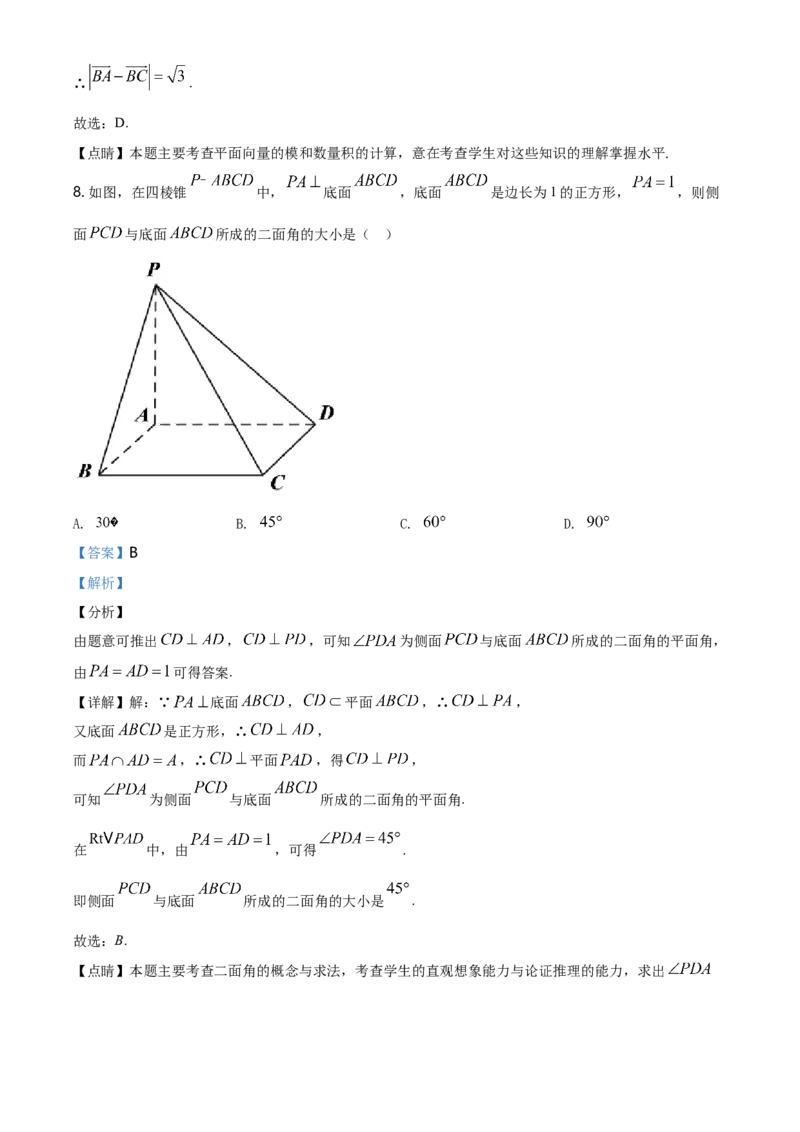
8. 如图,在四棱锥 中, 底面 ,底面 是边长为1的正方形, ,则侧
面 与底面 所成的二面角的大小是( )
A. B. C. D.
【答案】B
【解析】
【分析】
由题意可推出 , ,可知 为侧面 与底面 所成的二面角的平面角,
由 可得答案.
【详解】解:∵ 底面 , 平面 ,∴ ,
又底面 是正方形,∴ ,
而 ,∴ 平面 ,得 ,
可知 为侧面 与底面 所成的二面角的平面角.
在 中,由 ,可得 .
即侧面 与底面 所成的二面角的大小是 .
故选:B.
【点睛】本题主要考查二面角的概念与求法,考查学生的直观想象能力与论证推理的能力,求出为侧面 与底面 所成的二面角的平面角是解题的关键,属于基础题.
9. 已知平面向量 , 满足 , ,则“ 与 互相垂直”是“ ”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】D
【解析】
【分析】
由 与 互相垂直可得 ,进而得 ,即可判断.
【详解】∵ 与 互相垂直,
∴ ,
∴ ,∴ ,
故“ 与 互相垂直”是“ ”的既不充分也不必要条件.
故选:D.
【点睛】本题考查充分条件和必要条件的判断,涉及到向量垂直的转化,属于基础题.
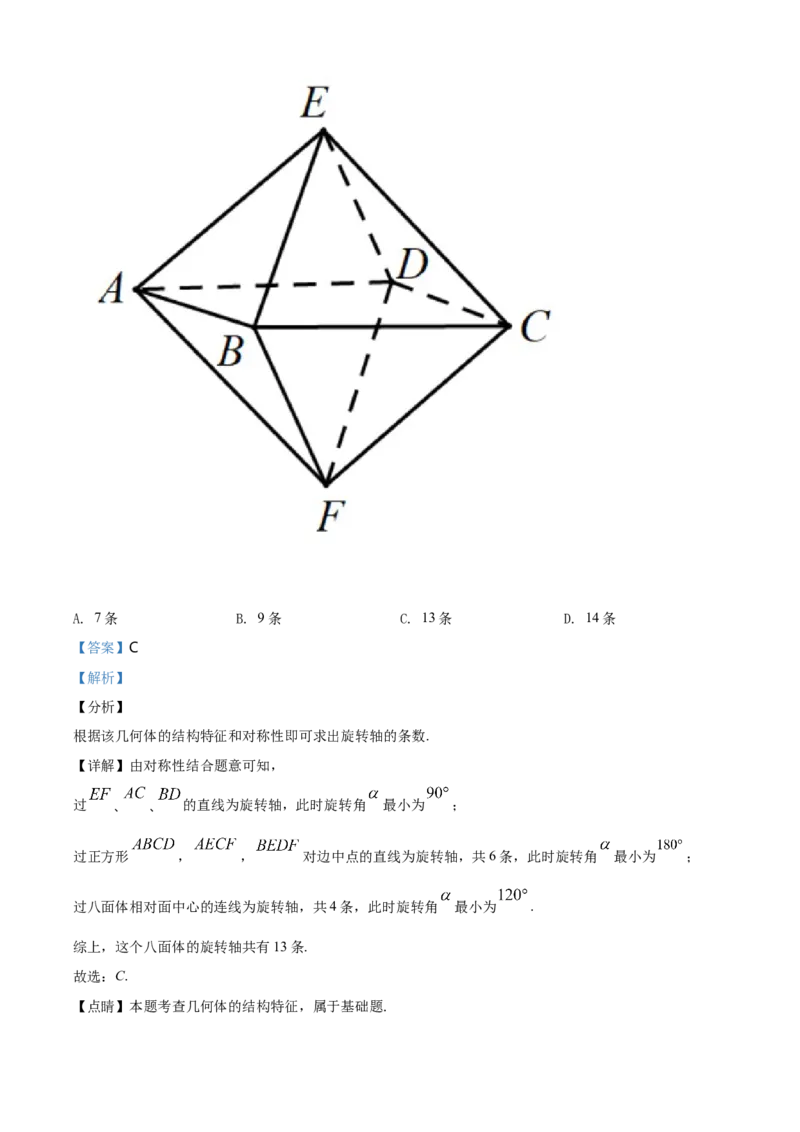
10. 连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角 ,使该几何体
与自身重合,那么称这条直线为该几何体的旋转轴.如图,八面体的每一个面都是正三角形,并且4个顶点
, , , 在同一平面内.则这个八面体的旋转轴共有( )A. 7条 B. 9条 C. 13条 D. 14条
【答案】C
【解析】
【分析】
根据该几何体的结构特征和对称性即可求出旋转轴的条数.
【详解】由对称性结合题意可知,
过 、 、 的直线为旋转轴,此时旋转角 最小为 ;
过正方形 , , 对边中点的直线为旋转轴,共6条,此时旋转角 最小为 ;
过八面体相对面中心的连线为旋转轴,共4条,此时旋转角 最小为 .
综上,这个八面体的旋转轴共有13条.
故选:C.
【点睛】本题考查几何体的结构特征,属于基础题.二、填空题(共6小题).
11. 复数 所对应的点在第______象限.
【答案】二
【解析】
【分析】
先求出复数 ,即可判断对应点所在象限.
【详解】∵ ,
∴复数 所对应的点的坐标为 ,在第二象限.
故答案为:二.
【点睛】本题考查复数的乘法运算,考查复数对应点的象限,属于基础题.
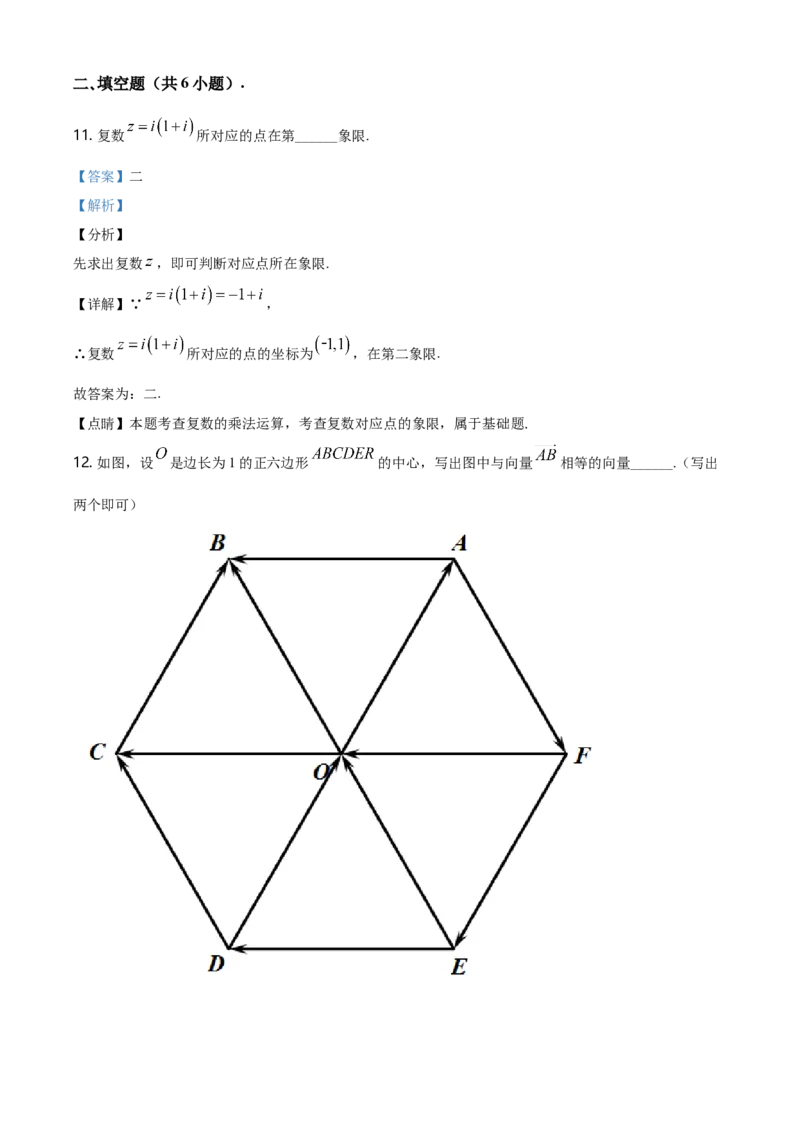
12. 如图,设 是边长为1的正六边形 的中心,写出图中与向量 相等的向量______.(写出
两个即可)【答案】 , ,
【解析】
【分析】
由题意与相等向量的定义可得答案.
【详解】解:由题可得:与 相等的向量是: , , ;
故答案为: , , .
【点睛】本题主要考查相等向量的定义,属于基础题.
13. 已知在平面直角坐标系中, , , 三点的坐标分别为 , , ,若 ,则
点 的坐标为______.
【答案】
【解析】
【分析】
设 ,求出 ,即可根据向量相等求出点 的坐标.
【详解】设 ,
则 , ;
因为 ,故 ;即 .
故答案为: .
【点睛】本题考查向量的坐标表示,属于基础题.
14. 某班数学兴趣小组组织了线上“统计”全章知识的学习心得交流:
甲同学说:“在频率分布直方图中,各小长方形的面积的总和小于1”;
乙同学说:“简单随机抽样因为抽样的随机性,可能会出现比较‘极端’的样本,相对而言,分层随机抽样的
样本平均数波动幅度更均匀”;
丙同学说:“扇形图主要用于直观描述各类数据占总数的比例”;
丁同学说:“标准差越大,数据的离散程度越小”.
以上四人中,观点正确的同学是______.【答案】乙丙
【解析】
【分析】
利用统计的相关知识可逐个判断各同学观点的正误.
【详解】在频率分布直方图中,各小长方形的面积的总和等于1,故甲的观点错误;
“简单随机抽样因为抽样的随机性,可能会出现比较‘极端’的样本,相对而言,分层随机抽样的样本平均数
波动幅度更均匀”,故乙的观点正确,
“扇形图主要用于直观描述各类数据占总数的比例”,故丙的观点正确;
“标准差越大,数据的离散程度越大”,故丁的观点错误.
故答案为:乙丙.
【点睛】本题考查统计的相关知识,属于基础题.
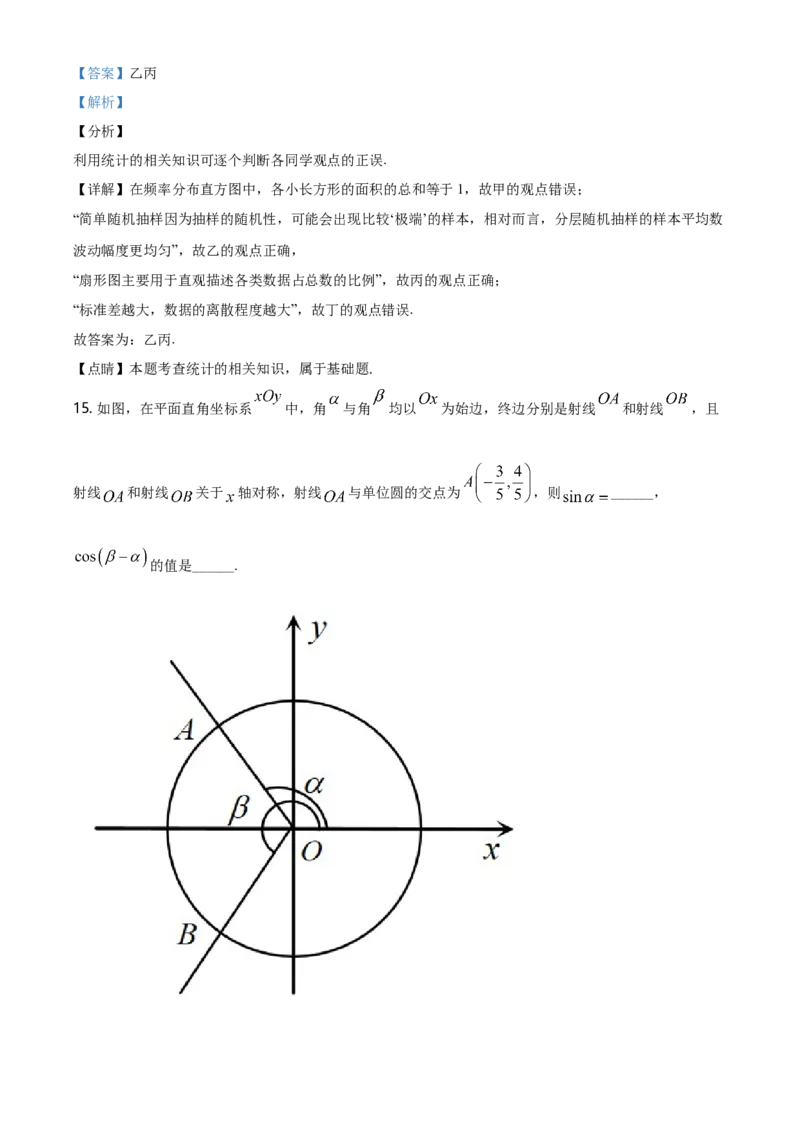
15. 如图,在平面直角坐标系 中,角 与角 均以 为始边,终边分别是射线 和射线 ,且
射线 和射线 关于 轴对称,射线 与单位圆的交点为 ,则 ______,
的值是______.【答案】 (1). (2).
【解析】
【分析】
利用三角函数的定义以及对称性可得出 、 的余弦值和正弦值,再利用两角差的余弦公式可求得
的值.
【详解】由题意,射线 与单位圆的交点为 ,射线 和射线 关于 轴对称,
射线 与单位圆的交点为 ,
由三角函数的定义可知, , , , ,
.
可得:
故答案为: , .
【点睛】本题考查利用两角差的余弦公式求值,同时也考查了三角函数定义的应用,考查计算能力,属于
基础题.
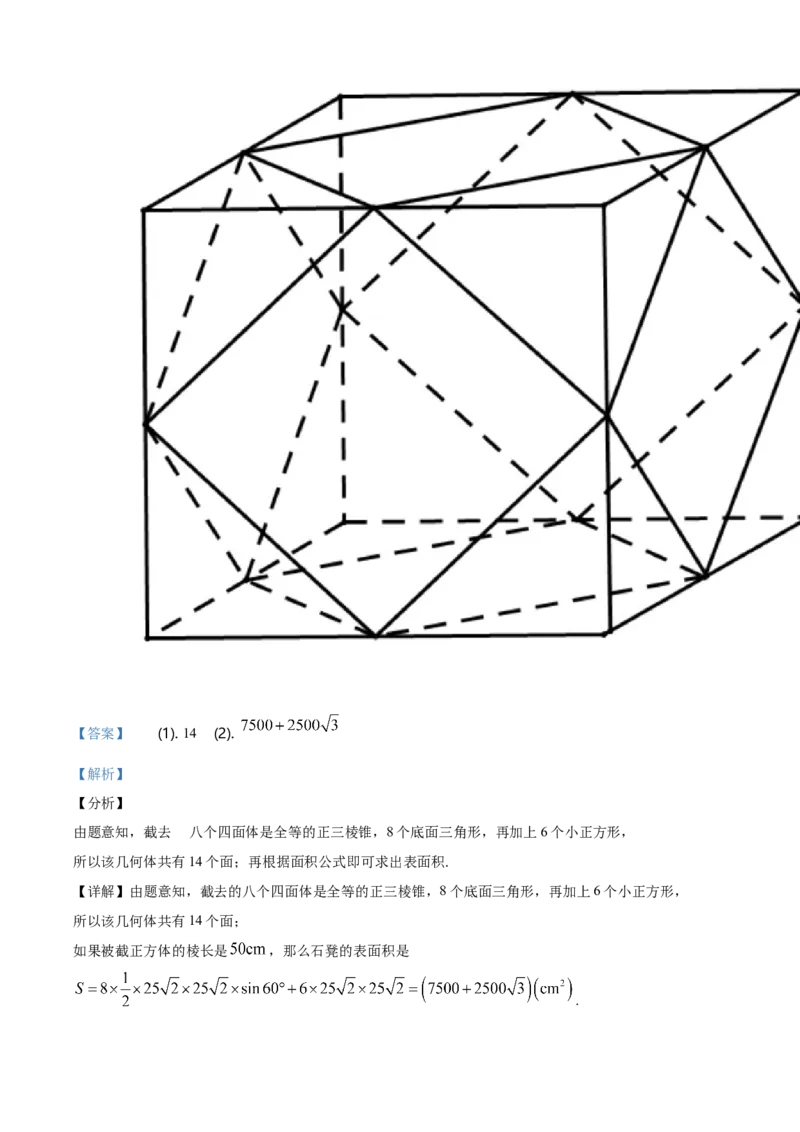
16. 某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的四面体得到的(如图).则
该几何体共有______面;如果被截正方体的棱长是 ,那么石凳的表面积是______ .【答案】 (1). 14 (2).
【解析】
【分析】
由题意知,截去 的八个四面体是全等的正三棱锥,8个底面三角形,再加上6个小正方形,
所以该几何体共有14个面;再根据面积公式即可求出表面积.
【详解】由题意知,截去的八个四面体是全等的正三棱锥,8个底面三角形,再加上6个小正方形,
所以该几何体共有14个面;
如果被截正方体的棱长是 ,那么石凳的表面积是
.故答案为:14, .
【点睛】本题考查几何体面数的辨析,考查多面体表面积的计算,属于基础题.
三、解答题:本大题共4小题,共70分.解答应写出文字说明,演算步骤或证明过程.
17. 某单位工会有500位会员,利用“健步行 ”开展全员参与的“健步走奖励”活动.假设通过简单随机抽
样,获得了50位会员5月10日的走步数据如下:(单位:万步)
1.1 1.4 1.3 1.6 0.3 1.6 0.9 1.4 1.4 0.9
1.4 1.2 1.5 1.6 0.9 1.2 1.2 0.5 0.8 1.0
.
1 4 0.6 1.0 1.1 0.6 0.8 0.9 0.8 1.1 0.4
0.8 1.4 1.6 1.2 1.0 0.6 1.5 1.6 0.90.7
1.3 1.1 0.8 1.0 1.2 0.6 0.5 0.2 0.8 1.4
频率分布表:
分组 频数 频率
2 0.04
0.06
5 0.10
11 0.22
8 0.16
7 0.14
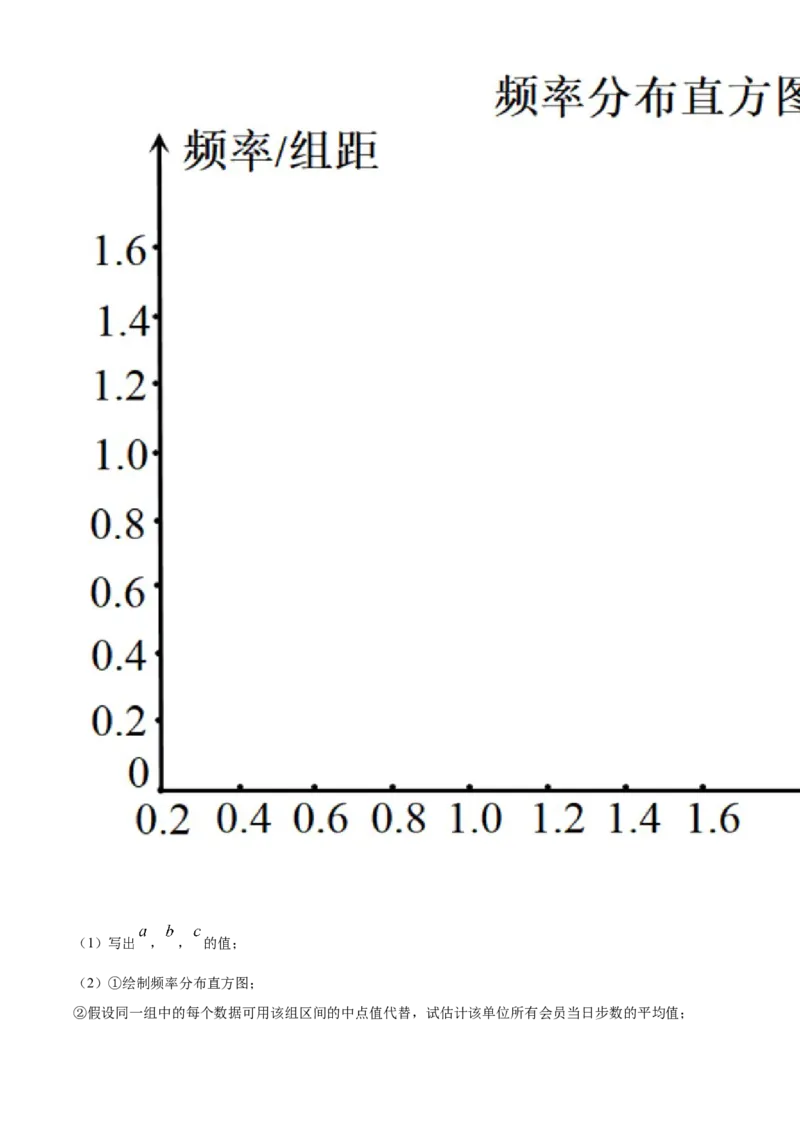
合计 50 1.00(1)写出 , , 的值;
(2)①绘制频率分布直方图;
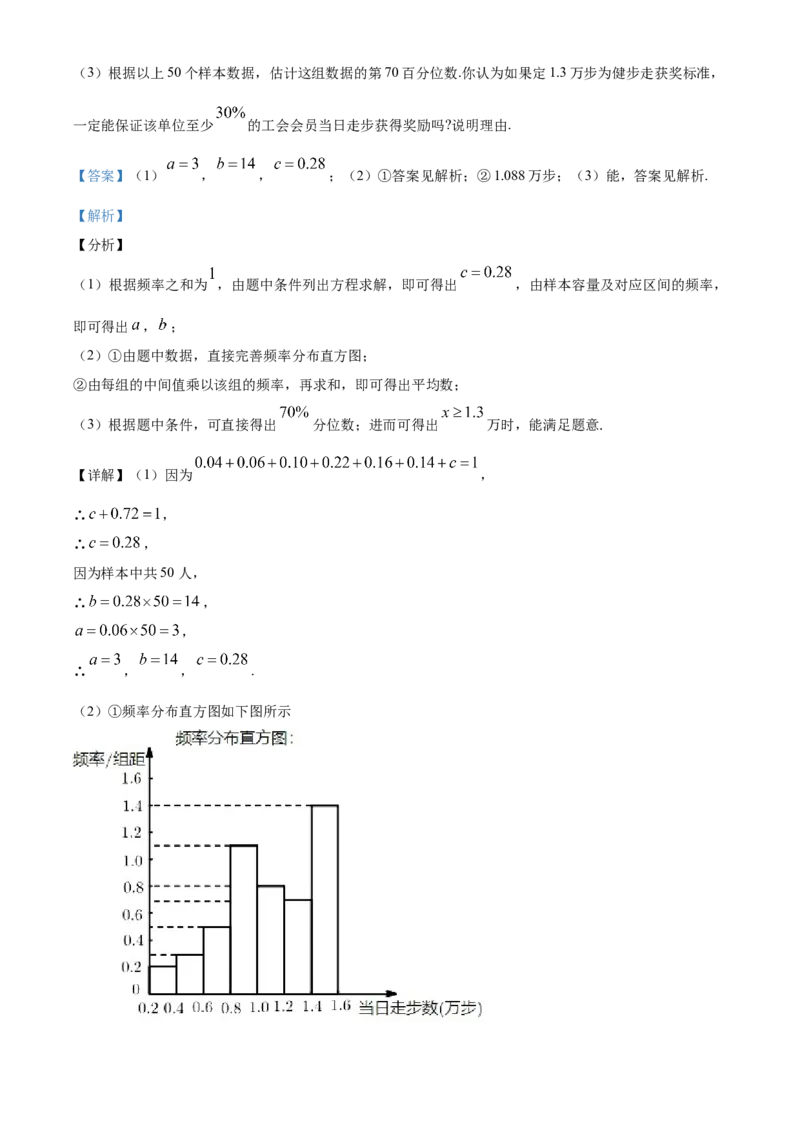
②假设同一组中的每个数据可用该组区间的中点值代替,试估计该单位所有会员当日步数的平均值;(3)根据以上50个样本数据,估计这组数据的第70百分位数.你认为如果定1.3万步为健步走获奖标准,
一定能保证该单位至少 的工会会员当日走步获得奖励吗?说明理由.
【答案】(1) , , ;(2)①答案见解析;②1.088万步;(3)能,答案见解析.
【解析】
【分析】
(1)根据频率之和为 ,由题中条件列出方程求解,即可得出 ,由样本容量及对应区间的频率,
即可得出 , ;
(2)①由题中数据,直接完善频率分布直方图;
②由每组的中间值乘以该组的频率,再求和,即可得出平均数;
(3)根据题中条件,可直接得出 分位数;进而可得出 万时,能满足题意.
【详解】(1)因为 ,
∴ ,
∴ ,
因为样本中共50 人,
∴ ,
,
∴ , , .
(2)①频率分布直方图如下图所示②设平均值为 ,则有
,
则该单位所有会员当日步数的平均值为1.088万步.
(3)∵ ,
∴ 分位数为第35和36个数的平均数,
∵ 共有14人,且1.3有2个,
∴ 第35和第36个数均为1.3,
∴ 分位数为1.3,
设 为会员步数,则 万时,人数不少于 ,
∴ 能保证 的工会会员获得奖励.
【点睛】本题主要考查完善频率分布表,考查画频率分布直方图,以及由频率分布直方图求平均数,属于
基础题型.
18. 在 中, , , 分别是角 , , 的对边, , .
(1)若 ,求 ;
(2)若______,求 的值及 的面积.
请从① ,② ,这两个条件中任选一个,将问题(2)补充完整,并作答.注意,只需选
择其中的一种情况作答即可,如果选择两种情况作答,以第一种情况的解答计分.
【答案】(1) ;(2)选①: ;选②: ; .
【解析】
【分析】(1)由正弦定理可直接得 值.
(2)选①:由余弦定理可求得 的值,然后利用三角形的面积公式计算可得结果.
选②: 由正弦定理可得 ,然后利用三角形的面积公式计算可得结果.
【详解】(1)由 , , ,
由正弦定理可得 ,则 .
(2) 若选①:由余弦定理可得 ,即 ,
整理可得 ,解得 , (舍去),
∴ ;
选②: ,可得 ,
∴
∴ .
【点睛】本题考查正弦定理和余弦定理以及三角形面积公式的应用,考查计算能力,属于基础题.
19. 已知函数 .
(1)求 的值;
(2)求 的最小正周期和单调递增区间;
(3)将函数 的图象向右平移 个单位,得到函数 的图象,若函数 在
上有且仅有两个零点,求 的取值范围.
【答案】(1)2;(2) ; , ;(3) .【解析】
【分析】
(1)利用二倍角公式和辅助角公式将函数化简,即可代入 ,求出结果;
(2)根据最小正周期的公式即可计算出周期,令 可解出单调递增区间;
(3)先求出 解析式,则该题等价于在 上有且仅有两个实数,满足 ,结合函
数图象即可求出 范围.
【详解】(1)∵函数 ,
∴ ,故
(2)由函数的解析式为 可得,它的最小正周期为 .
令 ,求得 ,
可得它的单调递增区间为 , .
(3)将函数 的图象向右平移 个单位,
得到函数 的图象,
若函数 在 上有且仅有两个零点,
则在 上有且仅有两个实数,满足 ,即 .
在 上, ,∴ ,求得 .
【点睛】本题考查三角恒等变换,考查最小正周期和单调区间的求解,考查三角函数的零点问题,属于中
档题.
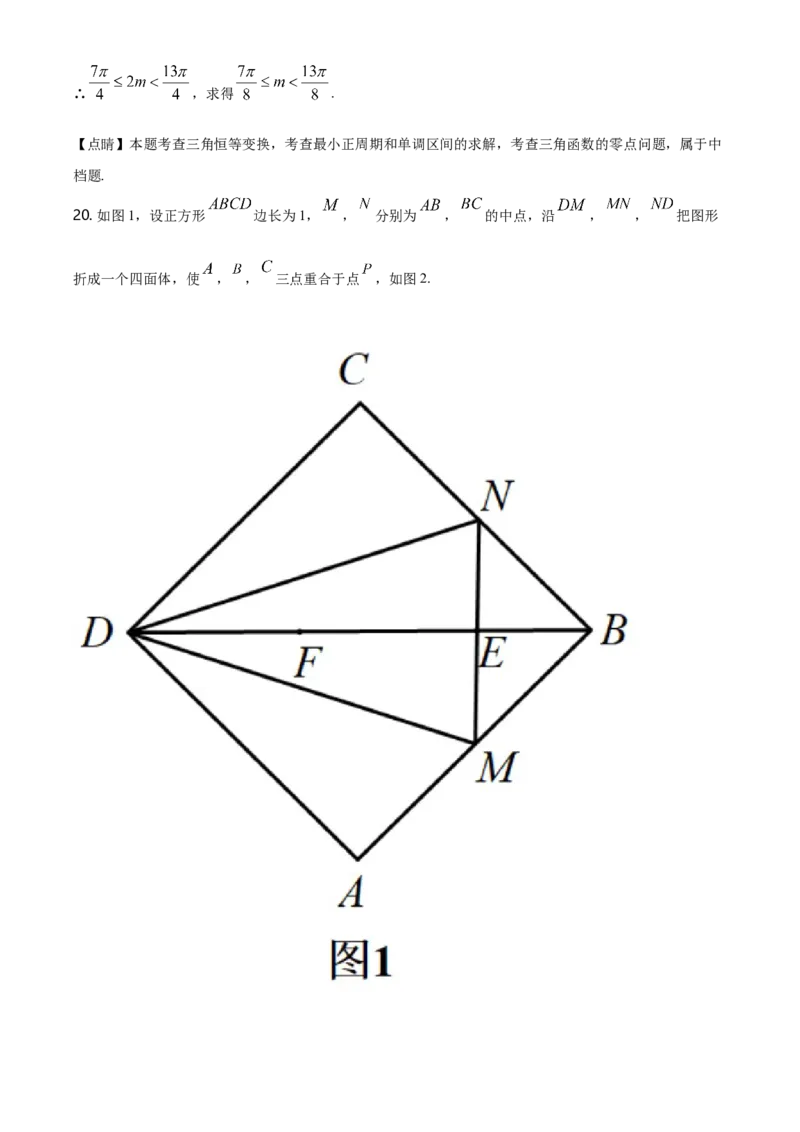
20. 如图1,设正方形 边长为1, , 分别为 , 的中点,沿 , , 把图形
折成一个四面体,使 , , 三点重合于点 ,如图2.(1)求证: 平面 ;
(2)设 为 的中点,在图2中作出过点 与平面 平行的平面 ,并说明理由;
(3)求点 到平面 的距离.
【答案】(1)证明见解析;(2)图象见解析;理由见解析;(3) .
【解析】
【分析】
(1)通过证明 和 即可证明 平面 ;
(2)根据面面平行的判断定理可作出图形并证明;
(3)利用等体积法可求出.
【详解】(1)证明:如图,在正方形 中,连接 ,则 ,∵ , 分别为 , 的中点,∴ ,
∴ ,折叠后,有 , ,
又 ,可得 平面 ;
(2)解:在平面 内,过 作 ,使得 , ,∵ 为 的中点,∴ , 分别为 , 的中点,
取 的中点 ,连接 , ,可得 ,
由 , 平面 , 平面 ,可得 平面 ,
同理可得, 平面 ,
又 , 平面 , 平面 ,
∴平面 平面 ,即平面 为所作平面 ;
(3)解:由已知可得, , ,
又 ,∴ 平面 ,且 等于正方形的边长为1,
, 为等腰直角三角形,
再由已知求得 , ,
∴ .
设点 到平面 的距离为 ,由 ,
可得 ,解得 ,
即点 到平面 的距离为 .
【点睛】本题考查线面垂直的证明,考查面面平行的判定,考查等体积法求点面距离,属于中档题.