黑龙江省哈尔滨师范大学附属中学2024-2025学年高一上学期期中考试数学PDF版含解析（可编辑）_2024-2025高一（7-7月题库）_2024年12月试卷

2024-2025 学年度高一上学期期中考试 数学试卷 一、单选题：本题共 8小题，每小题5分，共 40分．在每小题给出的四个选项中，只有一项是符合 题目要求的． 1. 命题 p:x 2 ，x2 0，则 p 是（ ） A. x 2，x2 0 B. x2，x2 0 C x2，x2 0 D. x2，x2 0 . 2. 已知集合M   y| yx22x  ，N  y| y log x  ，则M N （ ） 2 A. (0,1] B. (0,2] C. (,1] D. [1,) x2,x0  3. 若函数 f(x) 2 ，则 f[f(1)] （ ） x 5,x0  x A. 2 B.2 C. 4 D.4 4. 下列函数中，既不是奇函数，也不是偶函数的是（ ） A. y  1x2 B. y ln( 1x2 x) 1 C. y 2x  D. y xex 2x ln(1x) 5. 函数 f(x) 的定义域为（ ） 2x2 7x3 1 1 1 1 A. ( ,1) B. [ ,1) C. [ ,1] D. ( ,1] 2 2 2 2 6. 幂函数 f  x   m2 3m3  xm在区间  0, 上单调递减，则下列说法正确的是（ ） A. m4 B. m4 或 m1     C. f x 是奇函数 D. f x 是偶函数 1 7. 已知函数 f  x  x2  ，则不等式 f  2x1  f  x1  的解集为（ ） x2  1 1   1 1  A.  0,2  B.  0,2  C. 0,  ,2  D.  0,    ,2   2 2   2 2  3x2y1 8. 已知x,y为正实数，且x y 1，则 的最小值为（ ） xy A. 4 37 B. 2 23 C. 4 2 D. 6 第1页/共3页 学科网（北京）股份有限公司二、多选题：本题共 3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求， 全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 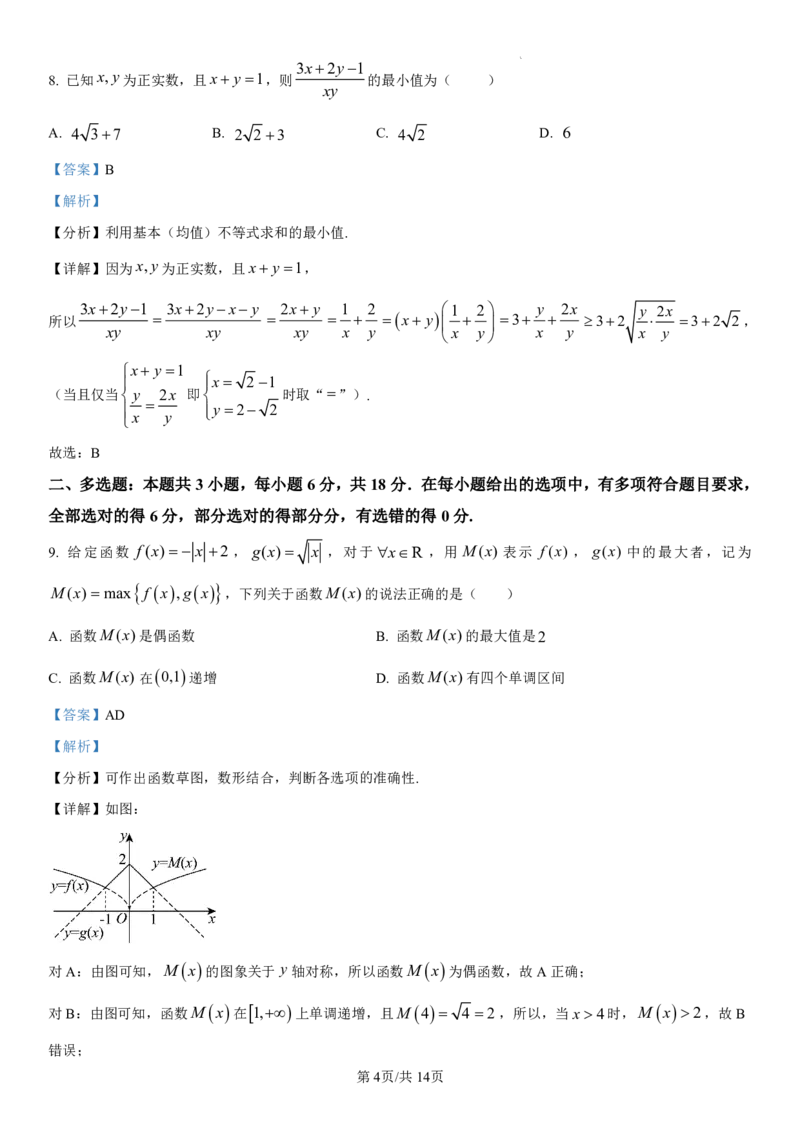9. 给定函数 f(x) x 2 ， g(x) x ，对于xR ，用 M(x) 表示 f (x) ， g(x) 中的最大者，记为 M(x)  max  f  x  ,g  x  ，下列关于函数M(x)的说法正确的是（ ） A. 函数M(x)是偶函数 B. 函数M(x)的最大值是2 C. 函数M(x)在0,1递增 D. 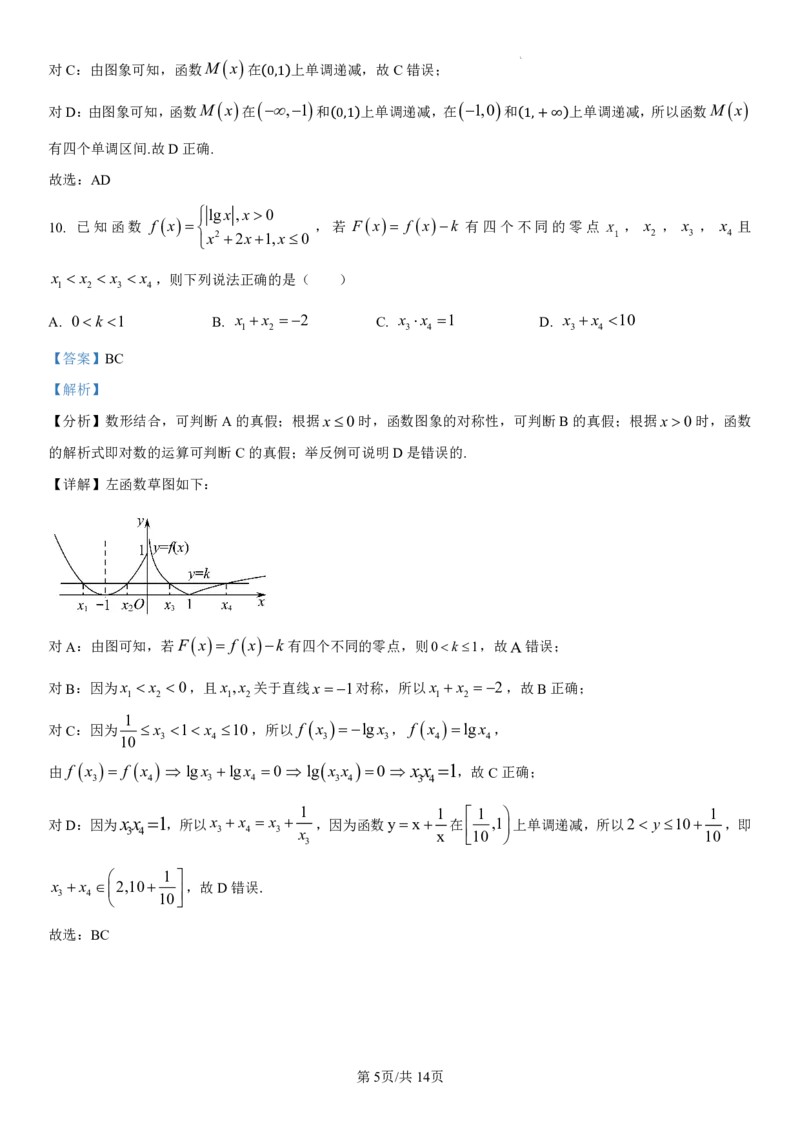函数M(x)有四个单调区间 lgx ,x0 10. 已知函数 f  x  ，若 Fx f xk 有四个不同的零点 x ， x ， x ， x 且 x2 2x1,x0 1 2 3 4 x  x  x  x ，则下列说法正确的是（ ） 1 2 3 4 A. 0k 1 B. x x 2 C. x x 1 D. x x 10 1 2 3 4 3 4 11. 高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德，牛顿并列为世界三 大数学家，用其名字命名的“高斯函数”为：对于实数x，符号 表示不超过x的最大整数，则 称为高斯函数， 例如  e  2， 1.8 2，定义函数 f  x  x x  ，则下列 说法正确的是（ ） =     A. 函数 f x 无最大值 B. 函数 f x 的最小值为1 C. 函数 f  x  在(2,1)上递增 D. f  x1  f  x  三、填空题：本题共 3小题，每小题 5分，共 15分． f(x)= log (x2- 4) 12. 函数 1 的单调递增区间为________． 2 13. 若不等式ax2 +ax-1<0对一切xR恒成立，则实数a的取值范围是____________ ． 14. 矩形 ABCD（ AB  AD ）的周长为24，把V ABC 沿 AC 向△ADC 折叠， AB 折过去后交CD于点P.当 AB______________时，三角形ADP的面积最大，最大值为_______________ ． 四、解答题：本题共 5小题，共 77分.解答题应写出文字说明、证明过程或演算步骤． 15. 计算下列各式的值： 2 0 0.5 （1） 1   1   16   1 3       21 2022  9  64 （2）log 4 27 lg25lg47log 7 2. 3 第2页/共3页 学科网（北京）股份有限公司16. 设a0且a 1，函数y log  1x log (3x)的图像过点  1,2  ． a a （1）求a的值及函数的定义域；  3 （2）求函数在区间  0,  上的最大值．  2 17. 如今中国已经成为全球最大的新能源汽车消费市场，并且建成了高效的协同产业体系，2024年上半年新能源汽 车销售469万辆，同比增长29.7%.某企业计划引进新能源汽车生产设备，通过市场分析，每生产x（千辆）获利W(x) 75(x2 3),0 x2  （万元），关系如下：W(x)750x ，该公司预计2024年全年其他成本总投入为30x万元.由市场  ,2 x6 1x 调研知，该种车销路畅通，供不应求.记2024年的全年利润为 f (x)（单位：万元）. （1）求函数 f (x) 的解析式； （2）当2024年产量为多少千辆时，该企业利润最大？最大利润是多少？请说明理由. 18. 已知函数 f  x 4x  m1 2x 1. （1）若m0，求 f  x  在区间 1,2  上的值域； （2）若方程 f  x 20有实根，求实数m的取值范围； 2x24x1 （3）设函数g  x    1  ，若对任意的x 1 1,2  ，总存在x 2  0,3 ，使得 f x 1 gx 2 ，求实数m的取 2 值范围. 19. 对于函数 y  f  x  ,xI ，若存在x I ，使得 f  x  x ，则称x 为函数y  f  x  的 “不动点”;若存在x I ， 0 0 0 0 0 使得 f  f  x   x ，则称x 为函数 y  f  x  的“稳定点”.记函数 y f(x)的“不动点”和“稳定点”的集合分别为 0 0 0     A和B，即A x f(x) x , B  x f(f(x)) x ． （1）设函数 f(x)2x1，求A和B； （2）证明：若 f (x)为连续的单调函数，则AB； （3）若 f  x  x2 a  xR,aR  ，存在a，使得A B，求实数a的取值范围． 第3页/共3页 学科网（北京）股份有限公司2024-2025 学年度高一上学期期中考试 数学试卷 一、单选题：本题共 8小题，每小题5分，共 40分．在每小题给出的四个选项中，只有一项是符合 题目要求的． 1. 命题 p:x 2 ，x2 0，则 p 是（ ） A. x 2，x2 0 B. x2，x2 0 C. x2，x2 0 D. x2，x2 0 【答案】D 【解析】 【分析】根据存在量词命题的否定是全称量词命题判断即可. 【详解】∵存在量词命题的否定是全称量词命题， ∴命题 p:x2，x2 0，则p是x 2，x2 0. 故选：D. 2. 已知集合M   y| yx22x  ，N  y| y log x  ，则M N （ ） 2 A. (0,1] B. (0,2] C. (,1] D. [1,) 【答案】C 【解析】 【分析】分别确定集合M 和N ，再根据交集的概念求M N . 【详解】因为M   y| yx22x    y|yx121  y|y1 ,1； N  y| y log x   , . 2 所以M N  ,1  . 故选：C x2,x0  3. 若函数 f(x) 2 ，则 f[f(1)] （ ） x 5,x0  x A. 2 B.2 C. 4 D.4 【答案】A 【解析】 【分析】根据分段函数的解析式代入求值即可. 第1页/共14页 学科网（北京）股份有限公司【详解】∵ f(1)(1)2 1， 2 ∴ f[f(1)] f(1)1 52. 1 故选：A. 4. 下列函数中，既不是奇函数，也不是偶函数的是（ ） A. y  1x2 B. y ln( 1x2 x) 1 C. y 2x  D. y xex 2x 【答案】D 【解析】 【分析】根据函数奇偶性的概念判断即可. 【详解】显然 y  1 x2 是偶函数，故A错误；          由ln 1x2 x ln 1x2 x ln 1x2 x2 ln10，知 y ln 1x2 x 是奇函数，故B错误； 1 1 1 1 由2x  2x 2x  2x 2x  ，知y 2x  是偶函数，故C错误； 2x 2x 2x 2x 1 令 p(x) xex，由 f  0 10知 y xex不是奇函数，由 f  1 1e01  f 1 知 y  xex不 e 是偶函数，故D正确. 故选：D. ln(1x) 5. 函数 f(x) 的定义域为（ ） 2x2 7x3 1 1 1 1 A. ( ,1) B. [ ,1) C. [ ,1] D. ( ,1] 2 2 2 2 【答案】A 【解析】 【分析】根据解析式有意义的条件列不等式组，解不等式组可得函数的定义域. x1 1x0  1 【详解】由题意：  1   x1. 2x2 7x30   x3 2 2 1 所以所求函数的定义域为：( ,1). 2 故选：A 第2页/共14页 学科网（北京）股份有限公司6. 幂函数 f  x   m2 3m3  xm在区间  0, 上单调递减，则下列说法正确的是（ ） A. m4 B. m4 或 m1     C. f x 是奇函数 D. f x 是偶函数 【答案】C 【解析】 【分析】利用幂函数的定义和单调性可求m的值，故可判断AB的正误，再根据奇偶性的定义可判断CD的正误. 【详解】函数 f  x   m2 3m3  xm为幂函数，则m2 3m31，解得m4或m1. 当m4时， f  x  x4在区间 上单调递增，不满足条件，排除A，B； 1 0,+∞ 1 所以 f  x  ，定义域  x|x0  关于原点对称，且 f(x) f(x) ， x x 所以函数 f (x)是奇函数，不是偶函数，故C正确，D错误. 故选：C. 1 7. 已知函数 f  x  x2  ，则不等式 f  2x1  f  x1  的解集为（ ） x2  1 1   1 1  A.  0,2  B.  0,2  C. 0,  ,2  D.  0,    ,2   2 2   2 2  【答案】D 【解析】 【分析】根据函数的单调性和奇偶性，把函数不等式转化为代数不等式求解即可. 1 【详解】因为 f  x  x2  ，x0， x2 1 1 所以 f x x 2   x2   f  x  ，所以函数 f  x  为偶函数； x 2 x2  1   1   1  设0 x  x ，则 f  x  f  x x2  x2    x x  x x  1 ， 1 2 2 1  2 x2   1 x2  2 1 2 1  x2x2  2 1 1 2 1 因为0 x  x ，所以x x 0，x x 0，1 0，所以 f  x  f  x 0，即 f  x  f  x  1 2 2 1 2 1 x2x2 2 1 2 1 1 2   所以函数 f x 在 上单调递增. 0,+∞ 由函数 f  x  为偶函数，所以函数 f  x  的图象关于 y 轴对称，在 ,0  上单调递减. 2x10 所以 f  2x1  f  x1    x10  0 x2且x 1 . 故选：D 2  2x1  x1  第3页/共14页 学科网（北京）股份有限公司3x2y1 8. 已知x,y为正实数，且x y 1，则 的最小值为（ ） xy A. 4 37 B. 2 23 C. 4 2 D. 6 【答案】B 【解析】 【分析】利用基本（均值）不等式求和的最小值. 【详解】因为x,y为正实数，且x y 1， 3x2y1 3x2yx y 2x y 1 2 1 2 y 2x y 2x 所以      x y     3  32  32 2， xy xy xy x y  x y x y x y x y 1   x 21 （当且仅当y 2x 即 时取“”）.   y 2 2 x y 故选：B 二、多选题：本题共 3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求， 全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9. 给定函数 f(x) x 2 ， g(x) x ，对于xR ，用 M(x) 表示 f (x) ， g(x) 中的最大者，记为 M(x)  max  f  x  ,g  x  ，下列关于函数M(x)的说法正确的是（ ） A. 函数M(x)是偶函数 B. 函数M(x)的最大值是2 C. 函数M(x) 在 0,1递增 D. 函数M(x)有四个单调区间 【答案】AD 【解析】 【分析】可作出函数草图，数形结合，判断各选项的准确性. 【详解】如图： 对A：由图可知，M  x  的图象关于 y 轴对称，所以函数M  x  为偶函数，故A正确； 对B：由图可知，函数M  x  在  1,上单调递增，且M  4  4 2，所以，当x 4时，M  x 2，故B 错误； 第4页/共14页 学科网（北京）股份有限公司  对C：由图象可知，函数M x 在 上单调递减，故C错误； 0,1 对D：由图象可知，函数M  x  在 ,1  和 上单调递减，在 1,0  和 上单调递减，所以函数M  x  0,1 1,+∞ 有四个单调区间.故D正确. 故选：AD lgx ,x0 10. 已知函数 f  x  ，若 Fx f xk 有四个不同的零点 x ， x ， x ， x 且 x2 2x1,x0 1 2 3 4 x  x  x  x ，则下列说法正确的是（ ） 1 2 3 4 A. 0k 1 B. x x 2 C. x x 1 D. x x 10 1 2 3 4 3 4 【答案】BC 【解析】 【分析】数形结合，可判断A的真假；根据x0时，函数图象的对称性，可判断B的真假；根据x 0时，函数 的解析式即对数的运算可判断C的真假；举反例可说明D是错误的. 【详解】左函数草图如下： 对A：由图可知，若F  x  f  x k 有四个不同的零点，则0k 1，故A错误； 对B：因为x  x 0，且x ,x 关于直线x1对称，所以x x 2，故B正确； 1 2 1 2 1 2 1 对C：因为  x 1 x 10，所以 f  x lgx ， f  x lgx ， 10 3 4 3 3 4 4 由 f  x  f  x   lgx lgx 0  lg  x x 0  xx 1，故C正确； 3 4 3 4 3 4 3 4 1 1  1  1 对D：因为x 3 x 4 1，所以x 3 x 4  x 3  x ，因为函数y x x 在  10 ,1  上单调递减，所以2 y 10 10 ，即 3  1  x 3 x 4    2,10 10   ，故D错误. 故选：BC 第5页/共14页 学科网（北京）股份有限公司11. 高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德，牛顿并列为世界三 大数学家，用其名字命名的“高斯函数”为：对于实数x，符号 表示不超过x的最大整数，则 称为高斯函数， 例如  e  2， 1.8 2，定义函数 f  x  x x  ，则下列 说法正确的是（ ） =     A. 函数 f x 无最大值 B. 函数 f x 的最小值为1 C. 函数 f  x  在(2,1)上递增 D. f  x1  f  x  【答案】ACD 【解析】 【分析】利用“高斯函数”的定义，得出 f  x  x x  的图象，结合图象，对各个选项分析判断，即可求解. 【详解】当x2,1  时， f  x  x x  x2，当x1,0  时， f  x  x x  x1， 当x0,1时， f  x  x x  x，当x 1,2  时， f  x  x x  x1， 当x2,3时，f  x  x x  x2，当x3,4时，f  x  x x  x3，L ，依此，可得 f  x  x x  的 图象如图所示， 由图知， f  x  的值域为  0,1  ，所以选项A正确，选项B错误， 对于选项C，因为当x2,1  时， f  x  x x  x2，所以函数 f  x  在(2,1)上递增，故选项C正确， 对于选项D，由图知， f  x  是周期函数，且 f  x1  f  x  ，所以选项D正确， 故选：ACD. 第6页/共14页 学科网（北京）股份有限公司三、填空题：本题共 3小题，每小题 5分，共 15分． f(x)= log (x2- 4) 12. 函数 1 的单调递增区间为________． 2 【答案】(,2) 【解析】   【分析】求 f x 的递增区间，根据复合函数单调性，即转化为求t  x2 4在定义域上的减区间. 【详解】由x2 40得 ,2    2, ，令t  x2 4，由于函数t  x2 4的对称轴为 y 轴，开口向上， y log t ∴t  x2 4在 上递减，在（0，＋∞）递增，又由函数 1 是定义域内的减函数，∴原函数在（-∞， 2 −∞,0 -2）上递增．故答案为（-∞，-2）. 【点睛】本题考查了复合函数单调区间的求法，属于基础题. 13. 若不等式ax2 +ax-1<0对一切xR恒成立，则实数a的取值范围是____________ ． 【答案】 4,0  【解析】 【分析】先分情况讨论a的符号，再由0可得a的取值范围. 【详解】因为不等式ax2 +ax-1<0对一切xR恒成立， 所以若a 0，则不等式可化为：10，对一切xR恒成立，故a 0满足题意； a0 若a0，则  -4