新结构19题模式2024届贵阳一模数学试题+答案(1)_2024年3月_013月合集_2024届新高考19题（九省联考模式）数学合集140套

贵阳市 2024 年高三年级适应性考试（一） 数学 2024.2 本试卷分第 I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分 150分.考试时间为 120分钟. 注意事项： 1.答卷前，考生务必将姓名､准考证号用钢笔填写在答题卡相应位置上. 2.回答第 I 卷时，选出每小题答案后，用铅笔将答题卡上对应题目的答案标号涂黑，如需改 动，用橡皮擦干净后，再选涂其它答案标号.写在本试卷上无效. 3.回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效. 4.请保持答题卡平整，不能折叠考试结束后，监考老师将试题卷､答题卡一并收回. 第 I 卷（选择题共 58分） 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是符 合题目要求的. 1.设集合A={ 1,3,5,6 } ,B={ 2,3,5,8 } ，则A∩B=（ ） { } { } { } { } A. 1,2,3,5,6,8 B. 3,5 C. 1,3 D. 2,8 2.已知z是复数，若 ( 1+i ) z =2，则z =（ ） A.1−i B.1+i C.2i D.2−2i 3.设等差数列 { a } 的前n项和为S ，已知a +a =14,a =27，则S =（ ） n n 2 8 15 12 A.150 B.140 C.130 D.120   4.向量a =( 6,2 ) 在向量b =( 2,−1 )上的投影向量为（ ）  1 A. ( 2,−1 ) B.1,−  C. ( 4,−2 ) D. ( 3,1 )  2 5.已知圆C:(x−1)2 +(y−2)2 =9，直线l:m ( x+ y+1 )+ y−x=0,m∈R，则下列说法正确的是（ ） A.直线l过定点 (−1,−1 ) B.直线l与圆C一定相交 C.若直线l平分圆C的周长，则m=−4 D.直线l被圆C截得的最短弦的长度为 3 6.2023年8月至10月贵州榕江举办了“超级星期六”全国美食足球友谊赛.已知第一赛季的第一个周六（8月 学科网（北京）股份有限公司26日）共报名了贵州贵阳烤肉队等3支省内和辽宁东港草莓队等3支省外美食足球代表队.根据赛程安排，在 8月26日举行三场比赛，每支球队都要参赛，且省内代表队不能安排在同一场，则比赛的安排方式有 （ ） A.6种 B.9种 C.18种 D.36种 π 7.将函数 f ( x )=sinx的图像先向右平移 个单位长度，再把所得函数图像上的每个点的纵坐标不变，横坐 3 1  π  标都变为原来的 (ω>0)倍，得到函数g ( x ) 的图像.若函数g ( x ) 在 − ,0上单调递增，则ω的取值范 ω  2  围是（ ）  1  1  1 ( ] A.0,  B.0,  C.0,  D. 0,1  6  3  2 8.已知 f ( x ) 是定义在R上的偶函数，且 f′( x )+ex也是偶函数，若 f ( a )> f ( 2a−1 ) ，则实数a的取值范 围是（ ） 1   1 A. (−∞,1 ) B. ( 1,+∞) C. ,1 D. −∞,  ∪( 1,+∞) 3   3 二､多项选择题：本题共 3个小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合 题目要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9.设样本数据1,3,5,6,9,11,m的平均数为x ，中位数为x ，方差为s2，则（ ） 0 A.若x =6，则m=7 B.若m=2024，则x =6 0 C.若m=7，则s2 =11 D.若m=12，则样本数据的80%分位数为11 10.已知a>0,b>0，且a+b=2，则（ ） 1 1 A.2a +2b 2 2 B. + 2 a b C.log 2 a+log 2 b1 D.a2 +b2 2 11.在三棱锥P−ABC中，PC ⊥平面ABC,PC = AB=3，平面ABC内动点D的轨迹是集合 M ={D| DA =2 DB}.已知C,D ∈M 且D 在棱AB所在直线上，i =1,2，则（ ） i i A.动点D的轨迹是圆 B.平面PCD ⊥平面PCD 1 2 学科网（北京）股份有限公司C.三棱锥P−ABC 体积的最大值为3 D.三棱锥P−DD C外接球的半径不是定值 1 2 第 II 卷（非选择题共 92分） 三､填空题：本题共 3小题，每小题 5分，共 15分. 1 12.已知tanα=2，则 =__________. sin2α 13.已知一个圆台的上､下底面半径分别为1和3，高为2 3.若圆台内有一个球，则该球体积的最大值为 __________.（球的厚度可忽略不计） x2 y2 14.设F,F 分别为椭圆C: + =1(a >b>0)的左､右焦点，B为椭圆C的上顶点，直线BF 与椭圆C 1 2 a2 b2 1   的另一个交点为A.若AF ⋅BF =0，则椭圆C的离心率为__________. 2 2 四､解答题：共 5个小题，满分 77分.解答应写出相应的文字说明，证明过程或演算步骤. 15.（本题满分13分） 记ABC的内角A,B,C的对边分别为a,b,c，已知asinC = 3ccosA. （1）求角A； （2）若a =2，求ABC面积的最大值. 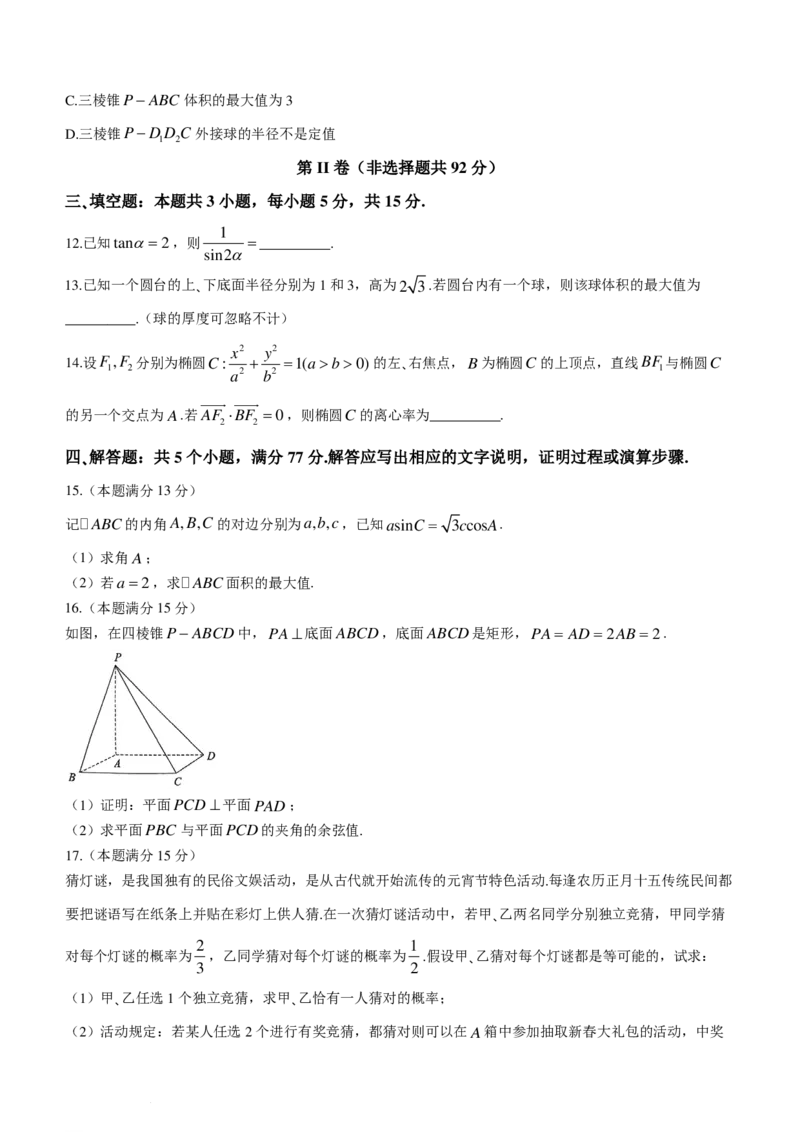16.（本题满分15分） 如图，在四棱锥P−ABCD中，PA⊥底面ABCD，底面ABCD是矩形，PA= AD=2AB=2. （1）证明：平面PCD⊥平面PAD； （2）求平面PBC 与平面PCD的夹角的余弦值. 17.（本题满分15分） 猜灯谜，是我国独有的民俗文娱活动，是从古代就开始流传的元宵节特色活动.每逢农历正月十五传统民间都 要把谜语写在纸条上并贴在彩灯上供人猜.在一次猜灯谜活动中，若甲､乙两名同学分别独立竞猜，甲同学猜 2 1 对每个灯谜的概率为 ，乙同学猜对每个灯谜的概率为 .假设甲､乙猜对每个灯谜都是等可能的，试求： 3 2 （1）甲､乙任选1个独立竞猜，求甲､乙恰有一人猜对的概率； （2）活动规定：若某人任选2个进行有奖竞猜，都猜对则可以在A箱中参加抽取新春大礼包的活动，中奖 学科网（北京）股份有限公司2 1 概率是 ；没有都猜对则在B箱中参加抽取新春大礼包的活动，中奖概率是 ，求甲同学抽中新春大礼包的 3 4 概率； （3）甲､乙各任选2个独立竞猜，设甲､乙猜对灯谜的个数之和为X ，求X 的分布列与数学期望. 18.（本题满分17分） x2 y2 已知双曲线C的方程为 − =1(a>0,b>0)，虚轴长为2，点A (−4,−1 ) 在C上. a2 b2 （1）求双曲线C的方程； （2）过原点O的直线与C交于S,T 两点，已知直线AS和直线AT 的斜率存在，证明：直线AS和直线AT 的斜率之积为定值； （3）过点 ( 0,1 ) 的直线交双曲线C于P,Q两点，直线AP,AQ与x轴的交点分别为M,N ，求证：MN 的 中点为定点. 19.（本题满分17分） 英国数学家泰勒发现了如下公式： x2 x3 xn ex =1+x+ + ++ + 2! 3! n! 其中n!=1×2×3×4××n,e为自然对数的底数，e=2.71828.以上公式称为泰勒公式.设 ex −e−x ex +e−x f ( x )= ,g ( x )= ，根据以上信息，并结合高中所学的数学知识，解决如下问题. 2 2 （1）证明：ex 1+x； ( ) f x （2）设x∈( 0,+∞) ，证明： < g ( x )； x  x2  （3）设F ( x )= g ( x )−a1+ ，若x=0是F ( x ) 的极小值点，求实数a的取值范围.  2  学科网（北京）股份有限公司贵阳市 2024 年高三年级适应性考试（一） 参考答案与评分建议 2024.2 一､选择题（每小题 5分，共 40分） 题号 1 2 3 4 5 6 7 8 答案 B A D C B D B D 二､多项选择题（每小题 6分，共 18分） 题号 9 10 11 答案 ABD ABCD ABC 三､填空题（每小题 5分，共 15分） 5 5 12. 13.4 3π 14. 4 5 四､解答题（共 5小题，共 77分） 15.解：（1）由正弦定理，得sinAsinC = 3sinCcosA， 又C∈( 0,π ) ,sinC ≠0，所以sinA= 3cosA， 即tanA= 3. π 又A∈( 0,π ) ，所以A= . 3 b2 +c2 −a2 1 （2）由余弦定理，得cosA= = ， 2bc 2 所以b2 +c2 −4=bc. 由基本不等式知b2 +c2 2bc， 于是bc=b2 +c2 −42bc−4⇒bc4. 当且仅当b=c=2时等号成立. 1 3 3 所以ABC的面积S = bcsinA= bc ×4= 3， 2 4 4 当且仅当b=c=2时，面积S取得最大值 3. 学科网（北京）股份有限公司16.（1）证明：因为PA⊥底面ABCD,CD⊂底面ABCD，所以PA⊥CD. 因为底面ABCD是矩形，所以AD⊥CD. 又PA∩AD= A，所以CD⊥平面PAD. 又因为CD⊂平面PCD，所以平面PCD⊥平面PAD. 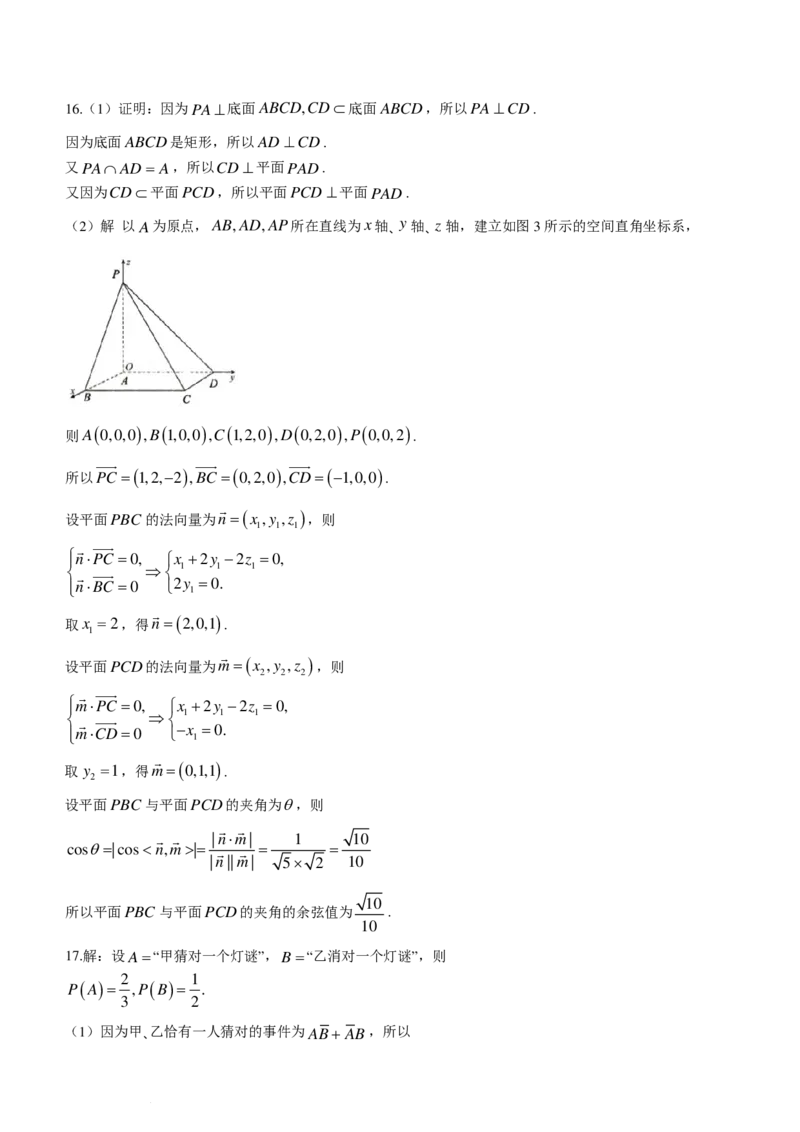（2）解 以A为原点，AB,AD,AP所在直线为x轴､y轴､z轴，建立如图3所示的空间直角坐标系， ( ) ( ) ( ) ( ) ( ) 则A 0,0,0 ,B 1,0,0 ,C 1,2,0 ,D 0,2,0 ,P 0,0,2 .    所以PC =( 1,2,−2 ) ,BC =( 0,2,0 ) ,CD=(−1,0,0 ) .  设平面PBC 的法向量为n =( x ,y ,z ) ，则 1 1 1    n⋅PC =0, x +2y −2z =0,   ⇒ 1 1 1 n⋅BC =0 2y 1 =0.  取x =2，得n =( 2,0,1 ) . 1  设平面PCD的法向量为m=( x ,y ,z ) ，则 2 2 2    m⋅PC =0, x +2y −2z =0,   ⇒ 1 1 1 m⋅CD=0  −x 1 =0.  取y =1，得m=( 0,1,1 ) . 2 设平面PBC 与平面PCD的夹角为θ，则     |n⋅m| 1 10 cosθ=|cos|=   = = |n||m| 5× 2 10 10 所以平面PBC 与平面PCD的夹角的余弦值为 . 10 17.解：设A=“甲猜对一个灯谜”，B=“乙消对一个灯谜”，则 2 1 P ( A )= ,P ( B )= . 3 2 （1）因为甲､乙恰有一人猜对的事件为AB+ AB，所以 学科网（北京）股份有限公司P(AB+ AB)= P(AB)+P(AB) = P(A)P(B)+P(A)P(B) 2 1 1 1 1 = × + × = . 3 2 3 2 2 1 所以，甲､乙恰有一人猜对的概率为 . 2 （2）设C =“甲猜对两道题”，D=“甲中奖”，则 P(D)= P(C)P(D∣C)+P(C)P(D∣C) 2  2 2 2 2 1 =   × +1−   × 3 3  3  4 8 5 47 = + = 27 36 108 47 所以，甲同学抽中新春大礼包的概率 . 108 2 1 （3）由（1）知P ( A )= ,P ( B )= . 3 2 易知甲､乙猜对灯谜的个数之和X 的可能取值为0,1,2,3,4.则 2 2 1 1 1 P ( X =0 )=   ×   = , 3 2 36 2 2 2 1 1 1 1 1 1 1 1 P ( X =1 )=C1× × ×   +C1× × ×   = + = , 2 3 3 2 2 2 2 3 9 18 6 2 2 2 2 2 1 1 1 2 1 1 1 13 P ( X =2 )=   ×   +   ×   +C1× × ×C1× × = , 3 2 3 2 2 3 3 2 2 2 36 2 2 2 1 1 1 1 2 1 P ( X =3 )=C1× × ×   +C1× × ×   = , 2 3 3 2 2 2 2 3 3 2 2 2 1 1 P ( x=4 )=   ×   = . 3 2 9 所以X 的分布列为 X 0 1 2 3 4 1 1 13 1 1 P 36 6 36 3 9 因此，X 的数学期望 学科网（北京）股份有限公司1 1 13 1 1 84 7 E ( X )=0× +1× +2× +3× +4× = = . 36 6 36 3 9 36 3 18.解：（1）因为虚轴长2b=2，所以b=1. 16 1 又因为点A (−4,−1 ) 在双曲线上，所以 − =1， a2 b2 解得a2 =8. x2 故双曲线C的方程为 − y2 =1. 8 （2）证明：设S ( x ,y ) ，则T (−x ,−y ) 0 0 0 0 所以 y +1 −y +1 1− y2 k ⋅k = 0 ⋅ 0 = 0 AS AT x +4 −x +4 16−x2 0 0 0 ( ) 因为S x ,y 在双曲线C上，所以 0 0 x2 x2 0 − y2 =1⇒1− y2 =2− 0 8 0 0 8 x2 2− 0 于是 1− y2 8 1， k ⋅k = 0 = = AS AT 16−x2 16−x2 8 0 0 1 所以直线AS和直线AT 的斜率之积为定值，定值是 . 8 （3）证明：设P ( x ,y ) ,Q ( x ,y ) ，直线PQ的方程为y =kx+1. 1 1 2 2 y =kx+1, ( )  ⇒ 1−8k2 x2 −16kx−16=0① x2 −8y2 =8 则 Δ=(−16k)2 −4 ( 1−8k2 ) ×(−16 )=64−256k2 >0, 所以 2 y + y =( kx +1 )+( kx +1 )=k ( x +x )+2= ② 1 2 1 2 1 2 1−8k2 y y =( kx +1 )( kx +1 )=k2x x +k ( x +x )+1=1③ 1 2 1 2 1 2 1 2 y +1 直线AP的方程为y = 1 ( x+4 )−1，令y =0，得点M 的横坐标为 x +4 1 学科网（北京）股份有限公司x +4 x = 1 −4 M y +1 1 同理可得点N 的横坐标为 x +4 x = 2 −4 N y +1 2 x +4 x +4 所以x +x = 1 + 2 −8 M N y +1 y +1 1 2 x y +x y +x +x +4 ( y + y )+8 = 1 2 2 1 1 2 1 2 −8 ( y +1 )( y +1 ) 1 2 x ( kx +1 )+x ( kx +1 )+x +x +4 ( y + y )+8 = 1 2 2 1 1 2 1 2 −8 y y + y + y +1 1 2 1 2 2kx x +2 ( x +x )+4 ( y + y )+8 = 1 2 1 2 1 2 −8. y y + y + y +1 1 2 1 2 将①②③式代入上式，并化简得到 ( ) 8+8 1−8k2 x +x = −8=4−8=−4, M N 2+2 ( 1−8k2 ) x +x 所以MN 的中点的横坐标为x= M N =−2， 2 故MN 的中点是定点 (−2,0 ) . 19.证明：（1）设h ( x )=ex −x−1，则h′( x )=ex −1. 当x>0时，h′( x )>0：当x<0时，h′( x )<0.所以h ( x ) 在 (−∞,0 ) 上单调递减，在 ( 0,+∞) 上单调递增. 因此，h ( x ) h ( 0 )=0，即ex 1+x. x2 x3 x4 x5 xn （2）由泰勒公式知ex =1+x+ + + + ++ +，① 2! 3! 4! 5! n! x2 x3 x4 x5 xn 于是e−x =1−x+ − + − ++(−1)n +，② 2! 3! 4! 5! n! 由①②得 ex −e−x x3 x5 x2n−1 f ( x )= = x+ + ++ +, 2 3! 5! ( 2n−1 ) ! 学科网（北京）股份有限公司ex +e−x x2 x4 x2n−2 g ( x )= =1+ + ++ +, 2 2! 4! ( 2n−2 ) ! 所以 f ( x ) x2 x4 x2n−2 =1+ + ++ + x 3! 5! ( 2n−1 ) ! x2 x4 x2n−2 <1+ + ++ + 2! 4! ( 2n−2 ) ! = g ( x ) . ( ) f x 即 < g ( x ) . x  x2  ex +e−x  x2  （3）F ( x )= g ( x )−a1+ = −a1+ ，则  2  2  2  ex −c−x ex +e−x F′( x )= −ax,F′′( x )= −a. 2 2 ex +e−x 1 由基本不等式知，  ×2 ex⋅e−x =1，当且仅当x=0时等号成立. 2 2 所以当a1时，F′′( x ) 1−a0，所以F′( x ) 在R.单调递增. 又因为F′( x ) 是奇函数，且F′( 0 )=0， 所以当x>0时，F′( x )>0；当x<0时，F′( x )<0. 所以F ( x ) 在 (−∞,0 ) 上单调递减，在 ( 0,+∞) 上单调递增. ( ) 因此，x=0是F x 的极小值点. ( ) 下面证明：当a >1时，x=0不是F x 的极小值点. elna +e−lna 1 1 11  当a >1时，F′′( lna )= −a = a+  −a =  −a <0， 2 2 a 2a  又因为F′′( x ) 是R上的偶函数，且F′′( x ) 在 ( 0,+∞) 上单调递增（这是因为当x>0时， 学科网（北京）股份有限公司所以当x∈(−lna,lna ) 时，F′′( x )<0. 因此，F′( x ) 在 (−lna,lna ) 上单调递减. 又因为F′( x ) 是奇函数，且F′( 0 )=0， 所以当−lna< x<0时，F′( x )>0；当0< x