文档内容
雅礼中学 2024 届高三一模
数学试卷
注意事项:
1.答卷前,考生务将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题(本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是符
合题目要求的)
1.已知集合U ={ 1,2,4,6,8 } ,集合M = { x∣x2 −3x+2=0 } ,N ={ x∣x=4a,a∈M } ,则 ( M ∪N )=
U
( )
{ } { } { } { }
A. 6 B. 4,6,8 C. 1,2,4,8 D. 1,2,4,6,8
1+z
2.设复数z满足 =−i,则 z =( )
1−z
2
A.i B. C.1 D. 2
2
3.已知m,n表示两条不同直线,α表示平面,则( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n⊂α,则m⊥n
C.若m⊥α,m⊥n,则n∥α
D.若m∥α,m⊥n,则n⊥α
4π
4.已知向量a = log 3,sin ,b =( log 8,m ) ,若a ⊥b ,则m=( )
2 3 3
A.−2 3 B.− 3 C.2 3 D.3 2
( )
5.函数 f x 的数据如下表,则该函数的解析式可能形如( )
x -2 -1 0 1 2 3 5
( )
f x 2.3 1.1 0.7 1.1 2.3 5.9 49.1
学科网(北京)股份有限公司A. f ( x )=kax +b B. f ( x )=kxex +b
C. f ( x )=k x +b D. f ( x )=k(x−1)2 +b
6.甲箱中有2个白球和4个黑球,乙箱中有4个白球和2个黑球.先从甲箱中随机取出一球放入乙箱中,以
A,A 分别表示由甲箱中取出的是白球和黑球;再从乙箱中随机取出一球,以B表示从乙箱中取出的是白
1 2
球,则下列结论错误的是( )
5
A.A,A 互斥 B.P ( B∣A )=
1 2 1 7
1 13
C.P
(
A B
)=
D.P
(
B
)=
2 7 21
7.已知等差数列 { a } (公差不为0)和等差数列 { b } 的前n项和分别为S ,T ,如果关于x的实系数方程
n n n n
1003x2 −S x+T =0有实数解,那么以下1003个方程x2 −a x+b =0 ( i =1,2,,1003 ) 中,有实数解
1003 1003 i i
的方程至少有( )个
A.499 B.500 C.501 D.502
8.双曲线C: x2 − y2 =1(a >0,b>0)的左、右焦点分别是F,F ,离心率为 6 ,点P ( x ,y ) 是C的右支上
a2 b2 1 2 2 1 1
异于顶点的一点,过F 作∠FPF 的平分线的垂线,垂足是M , MO = 2 ,若C上一点T 满足
2 1 2
FT⋅FT =5,则T 到C的两条渐近线距离之和为( )
1 2
A.2 2 B.2 3 C.2 5 D.2 6
二、多选题(本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分)
9.已知一组数据:12,31,24,33,22,35,45,25,16,若去掉12和45,则剩下的数据与原数据相比,下列结论
正确的是( )
A.中位数不变 B.平均数不变
C.方差不变 D.第40百分位数不变
π 2π
10.已知函数 f ( x )=sinωx+ 3cosωx(ω>0)满足: f =2, f =0,则( )
6 3
7π
A.曲线y = f ( x ) 关于直线x= 对称
6
π
B.函数y = f x− 是奇函数
3
学科网(北京)股份有限公司π 7π
C.函数y = f ( x ) 在 , 单调递减
6 6
D.函数y = f ( x ) 的值域为 [−2,2 ]
11.如图所示,有一个棱长为4的正四面体P−ABC容器,D是PB的中点,E是CD上的动点,则下列说
法正确的是( )
π
A.直线AE与PB所成的角为
2
B.ABE的周长最小值为4+ 34
6
C.如果在这个容器中放入1个小球(全部进入),则小球半径的最大值为
3
2 6−2
D.如果在这个容器中放入4个完全相同的小球(全部进入),则小球半径的最大值为
5
三、填空题(本题共 3小题,每小题 5分,共 15分)
6
1
12.在二项式( x−1 ) 2x+
的展开式中,常数项为__________.
x
13.已知圆锥的母线长为2,则当圆锥的母线与底面所成的角的余弦值为时__________,圆锥的体积最大,最
大值为__________.
a 2
14.对于任意两个正实数a,b,定义a⊗b=λ⋅ ,其中常数λ∈ ,1.若u≥v>0,且u⊗v与v⊗u都
b 2
n
是集合x x= ,n∈Z的元素,则u⊗v=__________.
2
四、解答题(本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.)
15.(13分)已知函数 f ( x )= x3−ax+a.
(1)若x=1是函数 f ( x ) 的极值点,求 f ( x ) 在 ( −1, f (−1 )) 处的切线方程.
( ) [ ]
(2)若a >0,求 f x 在区间 0,2 上最大值.
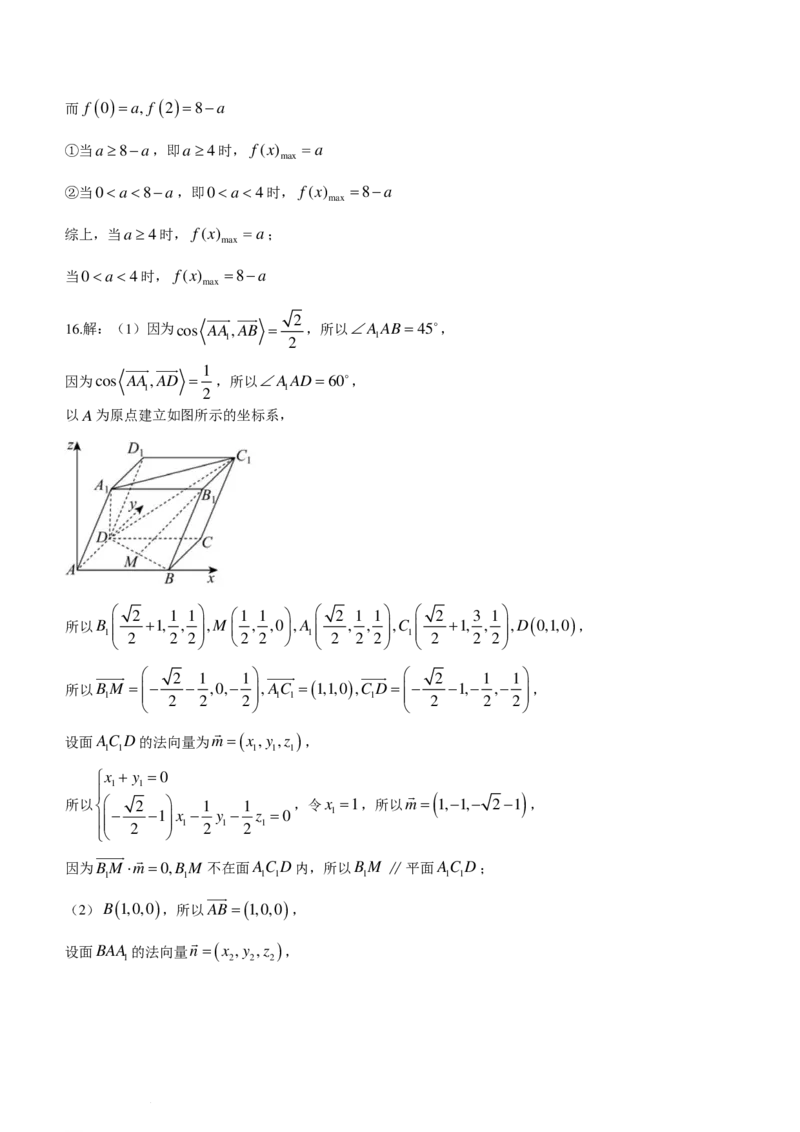
学科网(北京)股份有限公司16.(15分)如图,在平行六面体ABCD−ABC D 中,AB= AD= AA =1,∠DAB=90,
1 1 1 1 1
2 1
cos< AA,AB>= ,cos< AA,AD>= ,点M 为BD中点.
1 2 1 2
(1)证明:BM ∥平面AC D;
1 1 1
(2)求二面角B−AA −D的正弦值.
1
17.(15分)一个袋子中有10个大小相同的球,其中红球7个,黑球3个.每次从袋中随机摸出1个球,摸出
的球不再放回.
(1)求第2次摸到红球的概率;
(2)设第1,2,3次都摸到红球的概率为P;第1次摸到红球的概率为P ;在第1次摸到红球的条件下,第2
1 2
次摸到红球的概率为P ;在第1,2次都摸到红球的条件下,第3次摸到红球的概率为P .求P,P,P,P ;
3 4 1 2 3 4
(3)对于事件A,B,C,当P ( AB )>0时,写出P ( A ) ,P ( B∣A ) ,P ( C∣AB ) ,P ( ABC ) 的等量关系式,并加
以证明.
x2 y2 1 3
18.(17分)己知椭圆C: + =1(a >b>0)的离心率为 ,且点1,− 在椭圆上.
a2 b2 2 2
(1)求椭圆C的标准方程;
(2)如图,若一条斜率不为0的直线过点
(−1,0 )
与椭圆交于M,N 两点,椭圆C的左、右顶点分别为
k2 +k2
A,B,直线BN 的斜率为k ,直线AM 的斜率为k ,求证: 1 2 为定值.
1 2 k ⋅k
1 2
学科网(北京)股份有限公司19.(17分)约数,又称因数.它的定义如下:若整数a除以整数m ( m≠0 ) 除得的商正好是整数而没有余数,
我们就称a为m的倍数,称m为a的约数.设正整数a共有k个正约数,即为
a ,a ,,a ,a ( a 0时,由函数 f x 的数据可知,函数 f x 增长越来越快,可排除C.故选:A.
1
6.C 【解析】因为每次只取一球,故A,A 是互斥的事件,故A正确;由题意得P ( A )= ,
1 2 1 3
2 5 1 5 2 4 13
P ( A )= ,P ( B∣A )= ,P ( B )= P ( AB )+P ( A B )= × + × = ,故B,D均正确;因为
2 3 1 7 1 2 3 7 3 7 21
2 4 8
P ( A B )= × = ,故C错误.故选C.
2 3 7 21
1003 ( a +a )
7.D 【解析】由题意得:S2 −4×1003T 0,其中S = 1 1003 =1003a ,
1003 1003 1003 2 502
1003 ( b +b )
T = 1 1003 =1003b ,代入上式得:a2 −4b 0,
1003 2 502 502 502
要方程x2 −a x+b =0 ( i =1,2,3,,1003 ) 无实数解,则a2 −4b <0,显然第502个方程有解.设方程
i i i i
x2 −a x+b =0与方程x2 −a x+b =0的判别式分别为Δ ,Δ ,
1 1 1003 1003 1 1003
则Δ +Δ = ( a2 −4b ) + ( a2 −4b ) =a2 +a2 −4 ( b +b )
1 1003 1 1 1003 1003 1 1003 1 1003
( a +a )2 ( 2a )2
1 1003 −4×2b = 502 −8b =2 ( a2 −4b ) 0,
2 502 2 502 502 502
等号成立的条件是a =a ,所以Δ <0,Δ <0至多一个成立,
1 1003 1 1003
学科网(北京)股份有限公司同理可证:Δ <0,Δ <0至多一个成立,Δ <0,Δ <0至多一个成立,且Δ 0,
2 1002 501 503 502
综上,在所给的1003个方程中,无实数根的方程最多501个,故有实数解的方程至少有502个.故选:D.
8.A 【解析】设半焦距为c,延长F M 交PF 于点N ,由于PM 是∠FPF 的平分线,F M ⊥ PM ,所
2 1 1 2 2
以NPF 是等腰三角形,所以PN = PF∣,且M 是NF 的中点.
2 2 2
根据双曲线的定义可知 PF − PF =2a,即 NF =2a,由于O是FF 的中点,
1 2 1 1 2
1 6
所以MO是NFF 的中位线,所以|MO|= NF =a= 2 ,又双曲线的离心率为 ,
1 2 2 1 2
x2 ( ) ( )
所以c= 3,b=1,所以双曲线C的方程为 − y2 =1.所以F − 3,0 ,F 3,0 ,
1 2
2
( )
双曲线C的渐近线方程为x± 2y =0,设T u,v ,T 到两渐近线的距离之和为S,则
u+ 2v u− 2v ( )( )
S = + ,由FT⋅FT = u− 3 u+ 3 +v2 =u2 +v2 −3=5,得u2 +v2 =8,
1 2
3 3
x2 u2
又T 在C: − y2 =1上,则 −v2 =1,即u2 −2v2 =2,解得u2 =6,v2 =2,所以 u > 2 v ,故
2 2
2 u
S = =2 2,即距离之和为2 2.故选A.
3
9.AD 【解析】将原数据按从小到大的顺序排列为12,16,22,24,25,31,33,35,45,其
中位数为25,平均数是 ( 12+16+22+24+25+31+33+35+45 )÷9=27,方差是
1 824
×(−15)2 +(−11)2 +(−5)2 +(−3)2 +(−2)2 +42 +62 +82 +182 = ,由40%×9=3.6,得原数据的第
9 9
40百分位数是第4个数24.将原数据去掉12和45,得
186
16,22,24,25,31,33,35,其中位数为25,平均数是( 16+22+24+25+31+33+35 )÷7= ,方差是
7
2 2 2 2 2 2 2
1 74 32 18 11 31 45 59 1916
× − + − + − + − + + + = ,由40%×7=2.8,得新
7 7 7 7 7 7 7 7 49
数据的第40百分位数是第3个数24,故中位数和第40百分位数不变,平均数与方差改变,故A,D正确,
B,C 错误.故选:AD.
π
10.ABD 【解析】 f ( x )=2sin ωx+ ,所以函数y = f ( x ) 的值域为 [−2,2 ] ,故D正确;
3
学科网(北京)股份有限公司2π 2π π 3k −1 π
因为 f =0,所以 ω+ =k π,k ∈Z ,所以ω= 1 ,k ∈Z ,因为 f =2,所以
3 3 3 1 1 2 1 6
π π π 3k −1
ω+ = +2k π,k ∈Z,所以ω=12k +1,k ∈Z ,所以 1 =12k +1,即k =8k +1,所以
6 3 2 2 2 2 2 2 2 1 2
7π 7π π 3π
ω∈{ 1,13,25,37} ,因为 f =2sin ( 12k +1 ) + =2sin14k π+ =−2,所以曲线
6 2 6 3 2 2
7π
y = f ( x ) 关于直线x= 对称,故A正确;因为
6
π π π
f x− =2sin ( 12k +1 ) x− + =2sin (( 12k +1 ) x−4k π ) =2sin (( 12k +1 ) x ) 即
3 2 3 3 2 2 2
π π π
f x− =−f −x− ,所以函数y = f x− 是奇函数,故B正确;取ω=13,则最小正周期
3 3 3
2π 2π 7π π
T = = < − =π,故C错误.故选:ABD
ω 13 6 6
11.ACD 【解析】A选项,连接AD,由于D为PB的中点,所以PB⊥CD,PB⊥ AD,
又CD∩AD= D,AD,CD⊂平面ACD,所以直线PB⊥平面ACD,又AE ⊂平面ACD,
所以PB⊥ AE,故A正确;
B选项,把ACD沿着CD展开与平面BDC在同一个平面内,连接AB交CD于点E,则AE+BE的最小
值即为AB的长,由于AD=CD=2 3,AC =4,
CD2 + AD2 −AC2 (2 3)2 +(2 3)2 −42 1
cos∠ADC = = = ,
2CD⋅AD 2×2 3×2 3 3
π 2 2
cos∠ADB=cos +∠ADC =−sin∠ADC =− ,
2 3
2 2 16 6
所以AB2 = BD2 + AD2 −2BD⋅ADcos∠ADB=22 +(2 3)2 −2×2×2 3×− =16+ ,故
3 3
16 6 6 6
AB= 16+ =4 1+ ,ABE的周长最小值为4+4 1+ ,B错误;
3 3 3
C选项,要使小球半径最大,则小球与四个面相切,是正四面体的内切球,设球心为O,
学科网(北京)股份有限公司取AC的中点M ,连接BM,PM ,过点P作PF 垂直于BM 于点F ,则F 为ABC的中心,点O在PF
上,过点O作ON ⊥ PM 于点N ,因为AM =2,AB=4,所以
1 2 3
BM = AB2 −AM2 =2 3,同理PM =2 3,则MF = BM = ,故
3 3
4 6 4 6
PF = PM2 −MF2 = ,设OF =ON = R,故OP= PF −OF = −R,因为PNO∼PFM ,
3 3
4 6
−R
ON OP R 3 6
所以 = ,即 = ,解得R= ,C正确;
FM PM 2 3 2 3 3
3
D选项,4个小球分两层(1个,3个)放进去,要使小球半径要最大,则4个小球外切,且小球与三个平面
相切,设小球半径为r,四个小球球心连线是棱长为2r的正四面体Q−VKG,由C选项可知,其高为
2 6
r,由C选项可知,PF 是正四面体P−ABC 的高,PF 过点Q且与平面VKG交于S ,与平面HIJ
3
2 6 1
交于Z ,则QS = r,SF =r,由C选项可知,正四面体内切球的半径是高的 ,如图正四面体
3 4
2 6 6 2 6−2
P−HIJ 中,QZ =r,QP=3r ,正四面体P−ABC 高为3r+ r+r = ×4,解得r = ,D正
3 3 5
确.故选:ACD.
6 6 6 6
1 1 1 1
12.-160 【解析】( x−1 ) 2x+ = x2x+ − 2x+ ,因为 2x+ 的通项公式为
x x x x
k 6
1 1
T =Ck(2x)6−k =Ck26−kx6−2k ( 0k6,k∈N ),所以在x2x+ 中,当6−2k =−1时,不满
k+1 6 x 6 x
6
1
足;在 2x+
中,当6−2k =0时,k =3,则常数项为T =C323 =160,故答案为-160.
4 6
x
学科网(北京)股份有限公司6 16 3
13. ; π
3 27
【解析】设圆锥的底面半径r,母线为l,高为h,
π
设母线与底面所成的角为α 0<α< ,
2
r
则cosα= (00, f ( x ) 单调递增,
3
6
当x∈ ,1时, f′( x )<0, f ( x ) 单调递减,
3
6 ( )
所以当x= 时, f x 取得极大值,也是最大值.
3
8 6 16 3
此时V ( x )= π x4 −x6 最大,V =V = π,
3 max 3 27
6
即圆锥的母线与底面所成的角的余弦值cosα= 时,
3
16 3
圆锥的体积最大,最大值为 π.
27
6 16 3
故答案为: ; π.
3 27
3
14. /1.5
2
学科网(北京)股份有限公司 n
【解析】解:由u⊗v与v⊗u都是集合x x= ,n∈Z的元素,
2
u 1 v 1
不妨设u⊗v=λ⋅ = n ,v⊗u =λ⋅ = n ,n ,n ∈Z,
v 2 1 u 2 2 1 2
v
因为u≥v>0,所以0< ≤1,
u
2 1 v
由已知λ∈ ,1,所以 n =λ⋅ ∈( 0,1 ),则n ∈( 0,2 ) ,
2 2 2 u 2
1 λv
又n ∈Z,所以n =1,即 = ,
2 2
2 u
u 2
所以λ= ∈ ,1,
2v 2
u ( ) u2
所以 ∈ 2,2 , ∈( 2,4 ),
v v2
u u2 1 1
则λ⋅ = × = n ∈( 1,2 ),即n ∈( 2,4 ) ,
v v2 2 2 1 1
1 3 3
因为n ∈Z,所以n =3,则 n = ,即u⊗v= .
1 1 2 1 2 2
四、解答题(本题共 6小题,共 70分)
15.解:(1) f′( x )=3x2 −a,
( )
又x=1是函数 f x 的极值点,
∴ f′( 1 )=3−a=0,即a =3
∴ f ( x )= x3 −3x+3, f′( x )=3x2 −3
∴ f (−1 )=5, f′(−1 )=0
f ( x ) 在 ( −1, f (−1 )) 处的切线方程为y−5=0 ( x+1 ) ,即y =5,
所以 f ( x ) 在 ( −1, f (−1 )) 处的切线方程是y =5
(2) f′( x )=3x2 −a,令 f′( x )=0,得x=± a ,
3
a a
∴ f ( x ) 在0, 单调递减,在 ,+∞单调递增
3 3
学科网(北京)股份有限公司而 f
(
0
)=a,
f
(
2
)=8−a
①当a≥8−a,即a≥4时, f(x) =a
max
②当00,P (
AB
)>0,
( ) ( )
P AB P ABC
得P ( B∣A )= ,P ( C∣AB )= ,
( ) ( )
P A P AB
学科网(北京)股份有限公司( ) ( )
P AB P ABC
所以P ( A ) P ( B∣A ) P ( C∣AB )= P ( A )⋅ ⋅ = P ( ABC ) .
( ) ( )
P A P AB
x2 y2 1 3
18.(1)解:由椭圆C: + =1(a >b>0)的离心率为 ,且点1,− 在椭圆上,
a2 b2 2 2
c 1 b2 c2 1 2 3
可得 = ,所以 =1− =1−
= ,
a 2 a2 a2 2 4
3 1 9
又点1,− 在该椭圆上,所以 + =1,所以a2 =4,b2 =3,
2 a2 4b2
x2 y2
所以椭圆C的标准方程为 + =1.
4 3
(2)证明:设M ( x ,y ) ,N ( x ,y ) ,由于该直线斜率不为0,可设L :x=my−1,
1 1 2 2 MN
x2 y2
( )
联立方程x=my−1和 + =1,得 3m2 +4 y2 −6my−9=0,
4 3
Δ>0恒成立,根据韦达定理可知,
6m −9 3
y + y = ,y ⋅y = ,my ⋅y =− ( y + y ),
1 2 3m2 +4 1 2 3m2 +4 1 2 2 1 2
y y
k = 2 ,k = 1 ,
1 x −2 2 x +2
2 1
k y ( x −2 ) y ( my −3 ) my y −3y
2 = 1 2 = 1 2 = 1 2 1,
k ( x +2 ) y ( my +1 ) y my y + y
1 1 2 1 2 1 2 2
3
− ( y + y )−3y
k 2 1 2 1 k2 +k2 k k 10
∴ 2 = =3,∴ 1 2 = 1 + 2 = .
k 1 − 3 ( y + y )+ y k 1 ⋅k 2 k 2 k 1 3
2 1 2 2
19.解:(1)当k =4时正整数a的4个正约数构成等比数列,
比如1,2,4,8为8的所有正约数,即a =8.
a a
(2)由题意可知a =1,a =a,a = ,a = ,
1 k k−1 a k−2 a
2 3
a
a−
a −a a −a a −a a
因为k ≥4,依题意可知 3 2 = k k−1 ,所以 3 2 = 2 ,
a −a a −a a −a a a
2 1 k−1 k−2 2 1 −
a a
2 3
学科网(北京)股份有限公司2
a −a
化简可得( a −a )2 =( a −1 )2 a ,所以a = 3 2 ,
3 2 2 3 3 a −a
2 1
a −a
因为a ∈N*,所以 3 2 ∈N*,
3 a −a
2 1
因此可知a 是完全平方数.
3
由于a 是整数a的最小非1因子,a 是a的因子,且a >a ,所以a =a2,
2 3 3 2 3 2
所以a −a ,a −a ,,a −a 为a −1,a2 −a ,,ak−1−ak−2,
2 1 3 2 k k−1 2 2 2 2 2
所以a =ak−1, ( k4 ) .
2
(3)证明:由题意知aa =a,a a =a,,aa =a,, ( 1≤i≤k ) ,
1 k 2 k−1 i k+1−i
a2 a2 a2
所以A= + ++ ,
a a a a aa
k−1 k k−2 k−1 1 2
1 a −a 1 1 1 a −a 1 1
因为 ≤ 2 1 = − ,, ≤ k k−1 = − ,
aa aa a a a a a a a a
1 2 1 2 1 2 k−1 k k−1 k k−1 k
a2 a2 a2 1 1 1
所以A= + ++ =a2 + ++
a a a a aa a a a a aa
k−1 k k−2 k−1 1 2 k−1 k k−2 k−1 1 2
1 1 1 1 1 1 1 1
≤a2 − + − ++ − =a2 − ,
a a a a a a a a
1 2 2 3 k−1 k 1 k
1 1
因为a =1,a =a,所以 − <1,
1 k a a
1 k
1 1
所以A≤a2 −