文档内容
绝密 考试结束前
★
2023 学年第二学期浙南名校联盟返校联考
高二数学学科试题
考生须知:
1.本试题卷共 4页,满分 150分,考试时间 120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号.
3.所有答案必须写在答题卷上,写在试卷上无效.
4.考试结束后,只需上交答题卷.
选择题部分
一、选择题(本题共 8小题,每小题 5分,共 40分.在每小题所给的四个选项中,只有一项符合
题目要求.)
1.已知抛物线x2 =2py的焦点在直线y =2x+1上,则 p=( )
A.1 B.2 C.3 D.4
2.已知向量a =( 1,1,1 ) ,b =(−1,1,−2 ),则a在b 上的投影为( )
2 3 2 3 6 6
A.− B. C.− D.
3 3 3 3
3.已知点A ( 0,3 ) 及直线l:x+ y−1=0上一点B,则 AB 的值不可能是( )
A.1 B.2 C.3 D.4
4.已知数列 { a } 是各项为正的等比数列,前n项和为S ( n∈N* ) ,且S = 3 ,S = 7 ,则a =( )
n n 2 2 3 4 1
1 1 9
A. B. C.1 D.
4 2 4
5.若圆x2 −2ax+ y2 =0与圆x2 + y2 −4x−2y−4=0只有一个交点,则实数a的值可以是( )
A.-1 B.-2 C.1 D.2
6.已知ABC的三个内角分别为A,B,C,则lnA+lnB+lnC的值可能是( )
A.0.4 B.0.3 C.0.2 D.0.1
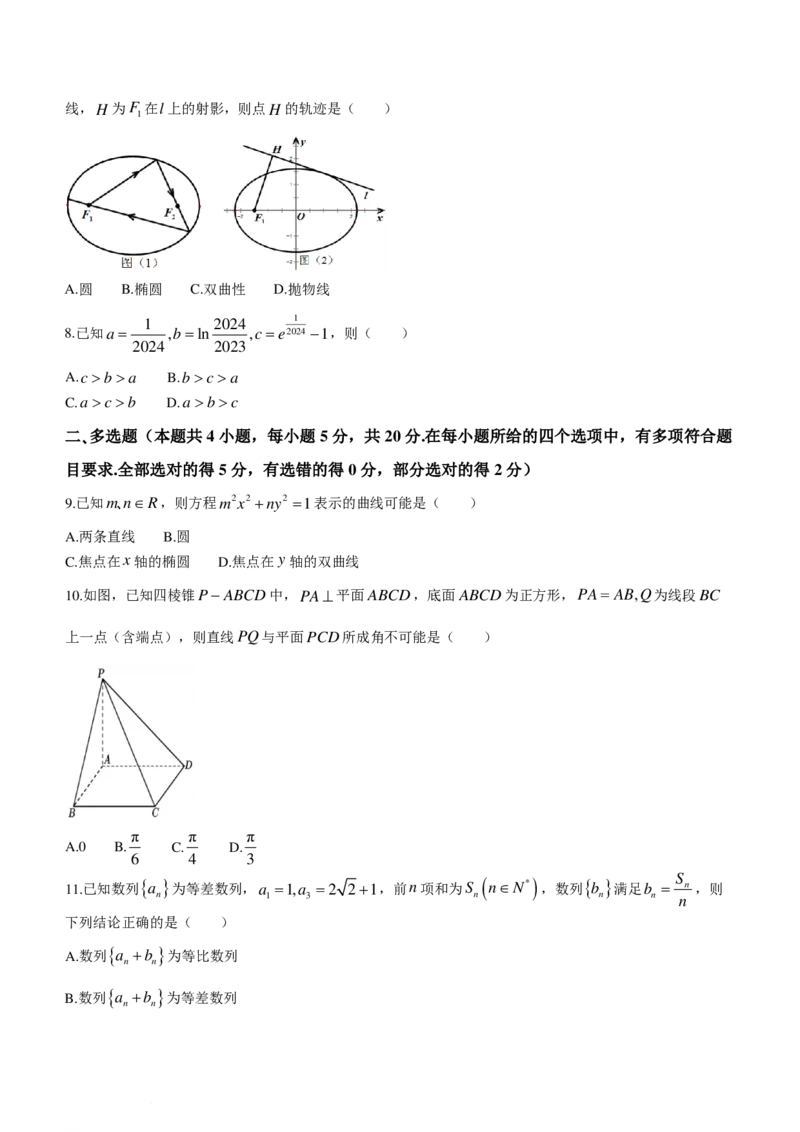
7.圆锥曲线具有丰富的光学性质,在人教版A版选择性必修第一册的阅读与思考中提到了椭圆的光学性质:
从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上,(如图(1)).如图
x2 y2
(2),已知F 为椭圆C: + =1(a>b>0)的左焦点,O为坐标原点,直线l为椭圆C的任一条切
1 a2 b2
学科网(北京)股份有限公司线,H 为F 在l上的射影,则点H 的轨迹是( )
1
A.圆 B.椭圆 C.双曲性 D.抛物线
1 2024 1
8.已知a = ,b=ln ,c=e2024 −1,则( )
2024 2023
A.c>b>a B.b>c>a
C.a>c>b D.a>b>c
二、多选题(本题共 4小题,每小题 5分,共 20分.在每小题所给的四个选项中,有多项符合题
目要求.全部选对的得5分,有选错的得 0分,部分选对的得 2分)
9.已知m、n∈R,则方程m2x2 +ny2 =1表示的曲线可能是( )
A.两条直线 B.圆
C.焦点在x轴的椭圆 D.焦点在y轴的双曲线
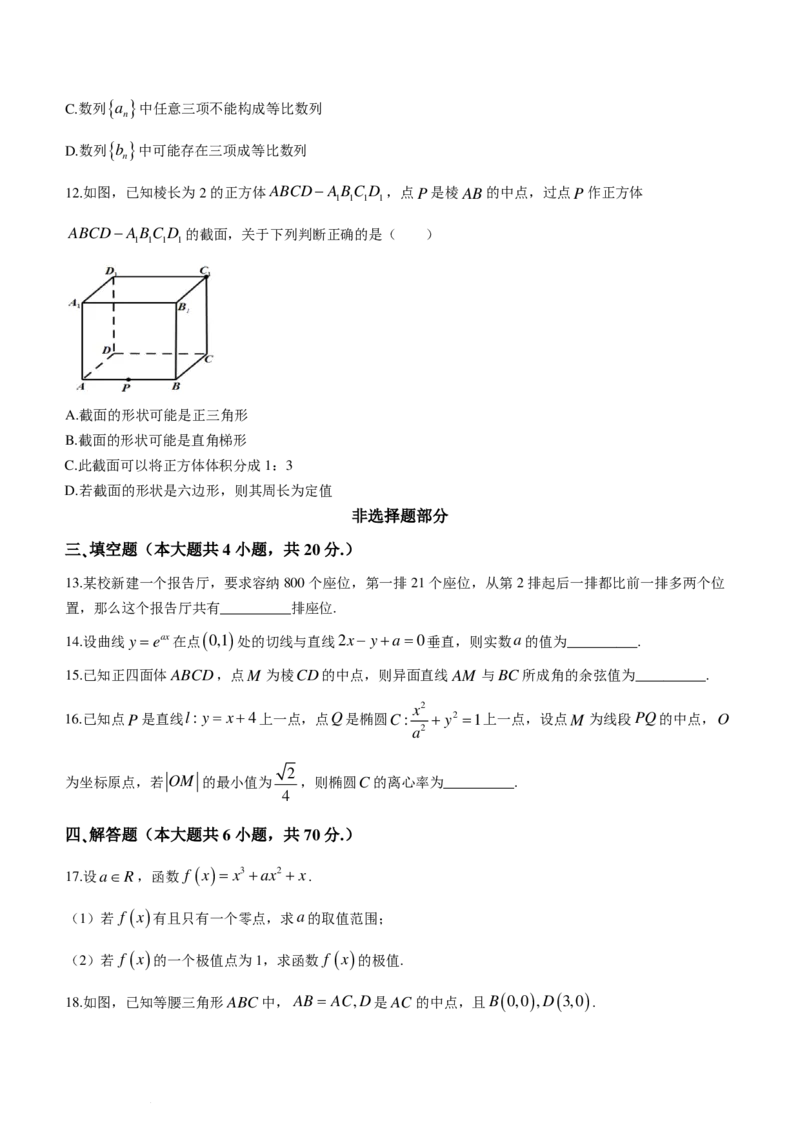
10.如图,已知四棱锥P−ABCD中,PA⊥平面ABCD,底面ABCD为正方形,PA= AB,Q为线段BC
上一点(含端点),则直线PQ与平面PCD所成角不可能是( )
π π π
A.0 B. C. D.
6 4 3
11.已知数列 { a } 为等差数列,a =1,a =2 2+1,前n项和为S ( n∈N* ) ,数列 { b } 满足b = S n ,则
n 1 3 n n n n
下列结论正确的是( )
A.数列 { a +b } 为等比数列
n n
B.数列 { a +b } 为等差数列
n n
学科网(北京)股份有限公司{ }
C.数列 a 中任意三项不能构成等比数列
n
{ }
D.数列 b 中可能存在三项成等比数列
n
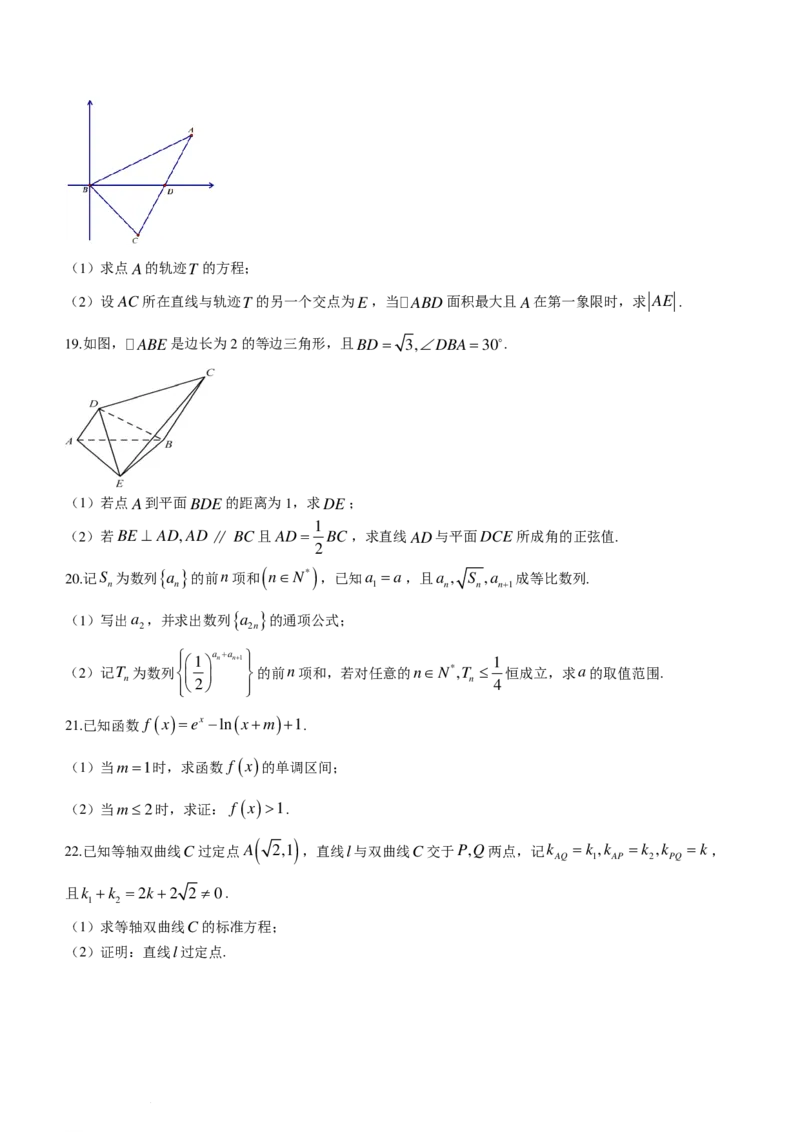
12.如图,已知棱长为2的正方体ABCD−ABC D ,点P是棱AB的中点,过点P作正方体
1 1 1 1
ABCD−ABC D 的截面,关于下列判断正确的是( )
1 1 1 1
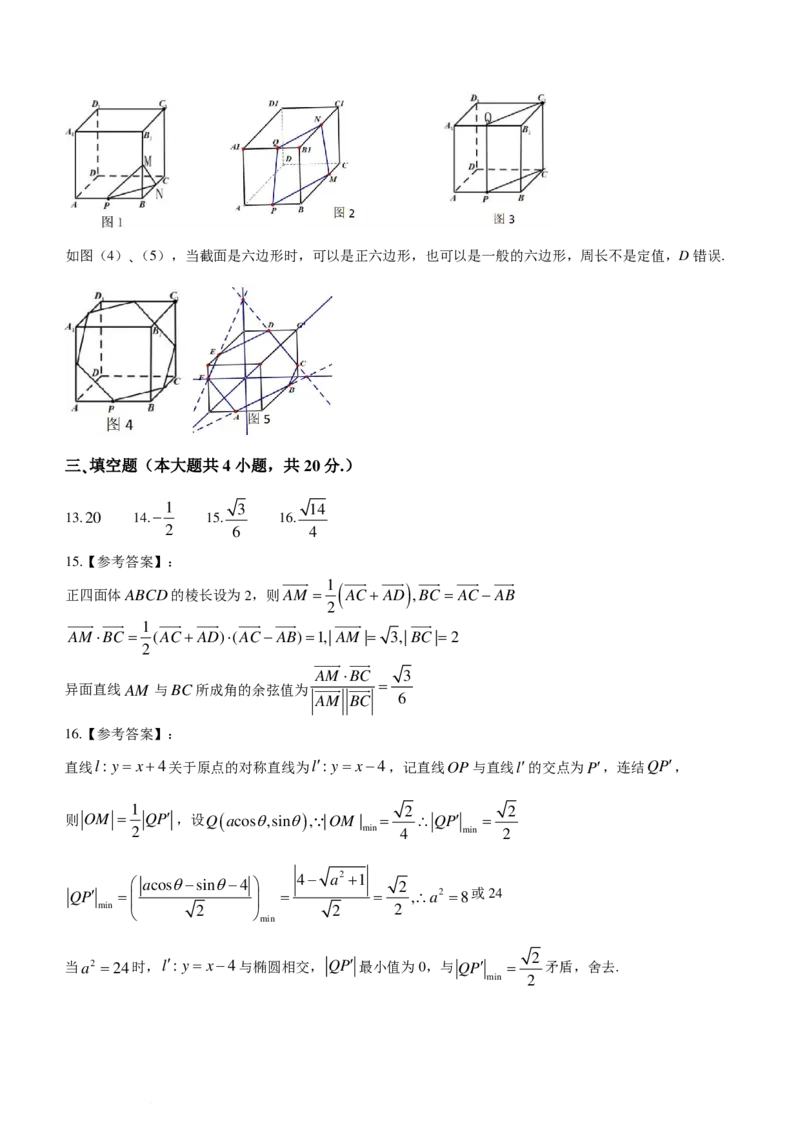
A.截面的形状可能是正三角形
B.截面的形状可能是直角梯形
C.此截面可以将正方体体积分成1:3
D.若截面的形状是六边形,则其周长为定值
非选择题部分
三、填空题(本大题共4小题,共 20分.)
13.某校新建一个报告厅,要求容纳800个座位,第一排21个座位,从第2排起后一排都比前一排多两个位
置,那么这个报告厅共有__________排座位.
14.设曲线y =eax在点 ( 0,1 ) 处的切线与直线2x− y+a=0垂直,则实数a的值为__________.
15.已知正四面体ABCD,点M 为棱CD的中点,则异面直线AM 与BC所成角的余弦值为__________.
x2
16.已知点P是直线l: y = x+4上一点,点Q是椭圆C: + y2 =1上一点,设点M 为线段PQ的中点,O
a2
2
为坐标原点,若 OM 的最小值为 ,则椭圆C的离心率为__________.
4
四、解答题(本大题共6小题,共 70分.)
17.设a∈R,函数 f ( x )= x3 +ax2 +x.
(1)若 f ( x ) 有且只有一个零点,求a的取值范围;
( ) ( )
(2)若 f x 的一个极值点为1,求函数 f x 的极值.
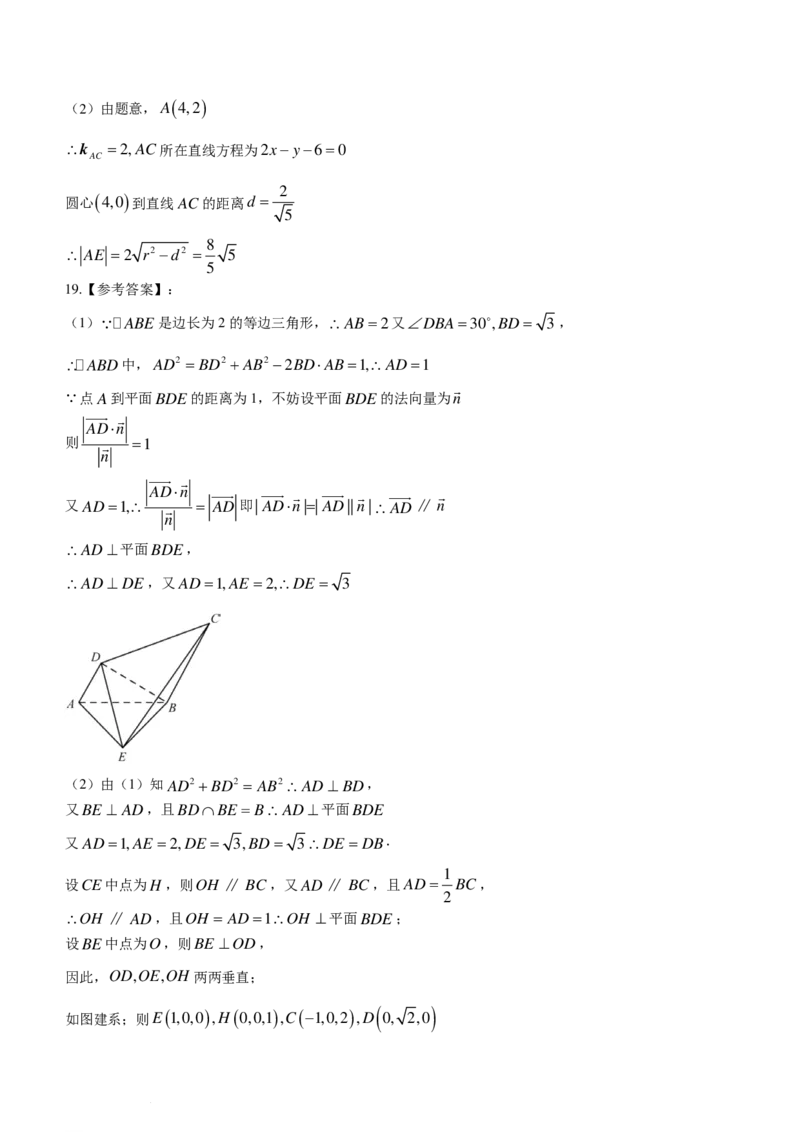
18.如图,已知等腰三角形ABC中,AB= AC,D是AC的中点,且B ( 0,0 ) ,D ( 3,0 ) .
学科网(北京)股份有限公司(1)求点A的轨迹T 的方程;
(2)设AC所在直线与轨迹T 的另一个交点为E,当ABD面积最大且A在第一象限时,求 AE .
19.如图,ABE是边长为2的等边三角形,且BD= 3,∠DBA=30.
(1)若点A到平面BDE的距离为1,求DE;
1
(2)若BE ⊥ AD,AD∥ BC且AD= BC,求直线AD与平面DCE所成角的正弦值.
2
20.记S 为数列 { a } 的前n项和 ( n∈N* ) ,已知a =a,且a , S ,a 成等比数列.
n n 1 n n n+1
{ }
(1)写出a ,并求出数列 a 的通项公式;
2 2n
1 a n +a n+1 1
(2)记T 为数列 的前n项和,若对任意的n∈N*,T ≤ 恒成立,求a的取值范围.
n 2 n 4
21.已知函数 f ( x )=ex −ln ( x+m )+1.
( )
(1)当m=1时,求函数 f x 的单调区间;
(2)当m≤2时,求证: f
(
x
)>1.
( )
22.已知等轴双曲线C过定点A 2,1 ,直线l与双曲线C交于P,Q两点,记k =k ,k =k ,k =k,
AQ 1 AP 2 PQ
且k +k =2k+2 2 ≠0.
1 2
(1)求等轴双曲线C的标准方程;
(2)证明:直线l过定点.
学科网(北京)股份有限公司高二数学学科参考答案与解析
一、选择题(本题共 8小题,每小题 5分,共 40分.在每小题所给的四个选项中,只有一项符合
题目要求.)
1 2 3 4 5 6 7 8
B C A C D D A B
二、多选题(本题共 4小题,每小题 5分,共 20分.在每小题所给的四个选项中,有多项符合题
目要求.)
9 10 11 12
ABC CD BC AC
6.【参考答案】:
由lnx≤ x−1得:lnA+lnB+lnC ≤ A+B+C−3=π−3<0.2,故选D
7.【参考答案】:
x x y y
解法一:设切线l与椭圆C相切于点P ( x ,y ) ,则切线l的方程是 0 + 0 =1,
0 0 a2 b2
a2y
则直线FH 的方程是y = 0 ( x+c ) ,
1 b2x
0
a2y b2x b4x2 2b2x
y = 0 ( x+c )⇒c= 0 y−x⇒a2 −b2 = 0 y2 +x2 − 0 xy
b2x a2y a4y2 a2y
0 0 0 0
y2 ( a2 −b2 ) x2 y2 2x y
⇒ 0 = 0 y2 + 0 x2 − 0 0 xy
b4 a4 b a2b2
4
x x y y y x2 2x y
1= 0 + 0 ⇒1= 0 y2 + 0 x2 + 0 0 xy
a2 b2 b4 a4 a2b2
⇒ y 0 2 ( a2 −b2 ) +1= x 0 2 + y 0 2 ( x2 + y2 )
b4 a4 b4
x2 y2 1 y2 y2 1 y2 ( a2 −b2 )
0 + 0 = 1− 0 + 0 = 1+ 0
a4 b4 a2
b2
b4 a2
b4
⇒ x2 + y2 =a2,故点H 的轨迹是圆.故选A
解法二:如图,设切线l与椭圆C相切于点P,过右焦点F
2
作F M ⊥l于M ,延长MO与直线FH 交于点N ,易知F M = FN,
2 1 2 1
学科网(北京)股份有限公司由椭圆光学性质知∠FPH =∠F PM ,
1 2
设∠FPH =θ,
1
则HM = PFcosθ+PFcosθ=2acosθ,
1 2
HN = PFsinθ+PFsinθ=2asinθ,所以MN =2a,
1 2
故OH =a,故选A.
1 2024 1
8.【参考答案】:a= ,b=ln ,c=e2024 −1
2024 2023
构造函数 f ( x )= x,g ( x )=−ln ( 1−x ) ,h ( x )=ex −1;x∈( 0,0.001 )
1 1 1
则a= f ,b= g ,c=h
2024 2024 2024
由于ex ≥ x+1(当且仅当x=0时取等号)恒成立,故c>a
由于ln ( x+1 )≤ x(当且仅当x=0时取等号)恒成立,
故ln
(−x+1 )≤−x(当且仅当x=0时取等号)
即−ln (−x+1 )≥ x(当且仅当x=0时取等号),故b>a
构造函数F ( x )=h ( x )−g ( x )=ex −1+ln ( 1−x ) ,x∈( 0,0.001 )
1 1
∴F′( x )=ex − ,∴F′′( x )=ex −
1−x (1−x)2
2
∴F′′′( x )=ex − ,当x∈( 0,0.001 ) 时,F′′′( x )<0
(1−x)3
1
∴F′′( x )=ex − 在x∈( 0,0.001 ) 上单调递减,∴F′′( x )< F′′( 0 )=0
(1−x)2
学科网(北京)股份有限公司1
∴F′( x )=ex − 在x∈( 0,0.001 ) 上单调递减,∴F′( x )< F′( 0 )=0
1−x
∴F ( x )=h ( x )−g ( x )=ex −1+ln ( 1−x ) 在 ( 0,0.001 ) 上单调递减
∴∀x∈(
0,0.001
)
,F
(
x
)=h (
x
)−g (
x
)<
F
(
0
)=0,∴cc>a,选B
11.【参考答案】:
a −a
(1)设数列 { a } 的公差为d,d = 3 1 = 2
n
2
n ( n−1 ) S 2 2
∴S =n+ × 2,∴b = n = n+1−
n 2 n n 2 2
∴数列 { b } 为等差数列,又数列 { a } 为等差数列
n n
∴数列 { a +b } 为等差数列.故B正确,A错误;
n n
(2)(反证法)假设数列 { a } 中存在三项a ,a ,a ( m,n, p∈N*,且m0, f ( x ) 单调递增
3
1 2
∴ f ( x )= f =− , f ( x )= f ( 1 )=−2
极大 极小
3 27
18.【参考答案】
解:
(1) AB =2 AD ,
即 x2 + y2 =2 (x−3)2 + y2 .
∴(x−4)2 + y2 =4 ( y ≠0 )
学科网(北京)股份有限公司( )
(2)由题意,A 4,2
∴k =2,AC所在直线方程为2x− y−6=0
AC
2
圆心 ( 4,0 ) 到直线AC的距离d =
5
8
∴ AE =2 r2 −d2 = 5
5
19.【参考答案】:
(1)ABE 是边长为2的等边三角形,∴AB =2又∠DBA=30,BD= 3,
∴ABD中,AD2 = BD2 + AB2 −2BD⋅AB=1,∴AD=1
点A到平面BDE的距离为1,不妨设平面BDE的法向量为n
AD⋅n
则 =1
n
AD⋅n
又AD=1,∴ = AD 即| AD⋅n|=| AD||n|∴AD ∥n
n
∴AD⊥平面BDE,
∴AD⊥ DE,又AD=1,AE =2,∴DE = 3
(2)由(1)知AD2 +BD2 = AB2∴AD⊥ BD,
又BE ⊥ AD,且BD∩BE = B∴AD⊥平面BDE
又AD=1,AE =2,DE = 3,BD= 3∴DE = DB⋅
1
设CE中点为H ,则OH ∥ BC,又AD∥ BC,且AD= BC,
2
∴OH ∥ AD,且OH = AD=1∴OH ⊥平面BDE;
设BE中点为O,则BE ⊥OD,
因此,OD,OE,OH 两两垂直;
( )
如图建系;则E
(
1,0,0
)
,H
(
0,0,1
)
,C
(−1,0,2 )
,D 0, 2,0
学科网(北京)股份有限公司
( )
∴EC =(−2,0,2 ) ,DC = −1,− 2,2 BC =2AD=2,AD∥ BC
1
∴AD= BC =OH,∴AD=OH =( 0,0,1 );
2
设平面DCE的法向量为n
=(
x,y,z
)
,则n⋅EC =0,n⋅DC =0,
2
∴−2x+2z =0,−x− 2y+2z =0,取x=1,则n =1, ,1
2
n⋅AD 10
∴sinθ= = .
n AD 5
20.【参考答案】:
(1)解:
由a , S ,a 成等比数列得a ⋅a =S ,且a >0,
n n n+1 n n+1 n n
当n=1时a ⋅a =a ⇒a =1;
1 2 1 2
当n≥2时,a ⋅a =S ,又a ⋅a =S
n−1 n n−1 n n+1 n
∴a =S −S =a ⋅a −a ⋅a ∴a −a =1 ( n≥2,n∈N )
n n n−1 n n+1 n−1 n n+1 n−1
a =a +( n−1 )×1=n ( n∈N* )
2n 2
(2)解法一:
n−1
a+ , n为奇数
2
由(1)易得a = ,
n n
, n为偶数
2
a+n
1
,n为奇数
2 1 a+n
则b
n
=
1 a+n
,故b
n
=
2
,n∈N*
,n为偶数
2
学科网(北京)股份有限公司1 a 1 n 1 a
∴T n = 2 1− 2 ,而T n < 2
a
1 1
∴
≤ ∴a≥2.
2 4
解法二:
1 a n +a n+1 1 a n+1 +a n+2 b 1 a n+2 −a n 1
设b = ,则b = ;∴ n+1 = =
n 2 n+1 2 b 2 2
n
∴{
b
}
是一个等比数列
n
a+1 n−1
1 1
∴b =
,n∈N*
n 2 2
1 a 1 n 1 a
∴T n = 2 1− 2 ,而T n < 2
a
1 1
∴
≤ ∴a≥2.
2 4
21.【参考答案】:
1
(1)当m=1时, f ( x )=ex −ln ( x+1 )+1,∴ f′( x )=ex −
x+1
1 1
∴ f′′( x )=ex + >0,故 f′( x )=ex − 在 (−1,+∞) 单调递增,
(x+1)2 x+1
又
f′(
0
)=0,∴x∈(−1,0 )
时,
f′(
x
)<0,∴x∈( 0,+∞)
时,
f′(
x
)>0
∴函数 f ( x ) 的单调递减区间为 (−1,0 ) ,单调递增区间为 ( 0,+∞)
(2)当m≤2时, f ( x )=ex −ln ( x+m )+1≥ex −ln ( x+2 )+1
1
令g ( x )=ex −ln ( x+2 )+1,则g′( x )=ex − ,
x+2
1
∴g′′( x )=ex + >0
(x+2)2
∴y = g′( x ) 在 (−2,+∞) 单调递增,又g′(−1 )<0,g′( 0 )>0,
∴∃x ∈(−1,0 ) ,使得g′( x )=0,且是y = g′( x ) 在 (−2,+∞) 上的唯一零点,
0 0
∴g′(
x
)
在
(−2,x )
上为负,在
(
x
,+∞)
上为正,
0 0
学科网(北京)股份有限公司故g ( x ) 在x= x 处取到极小值,也就是最小值.
0
1
g′( x )=0,即ex 0 = ,∴x =−ln ( x +2 ) ,x ∈(−1,0 )
0 x +2 0 0 0
0
1 1
∴g ( x )≥ g ( x )=ex 0 −ln ( x +2 )+1= +x +1= +( x +2 )−1>2−1
0 0 x +2 0 x +2 0
0 0
∴当m≤2时,求证: f ( x )>1.
22.【参考答案】
解:
(1)设等轴双曲线C:x2 − y2 =λ(λ≠0 ) ;
( )
C过A 2,1 ,∴λ=1∴C的标准方程为x2 − y2 =1.
(2)证明:设直线l的方程为 y =kx+m;
x2 − y2 =1
( ) ( )
联立方程: ⇒ k2 −1 x2 +2kmx+ m2 +1 =0
y =kx+m
( ) ( )
−2km m2 +1
设Q x ,y ,P x ,y ,则x +x = ;x x = ;(Δ>0)
1 1 2 2 1 2 k2 −1 1 2 k2 −1
( ) ( )
y −1 y −1 ( kx 1 +m−1 ) x 2 − 2 +( kx 2 +m−1 ) x 1 − 2
k +k = 1 + 2 =
1 2 x − 2 x − 2 x x − 2 ( x +x )
1 2 1 2 1 2
( )
2kx x + m−1− 2k ( x +x )−2 2 ( m−1 )
1 2 1 2
= =2k+2 2
x x − 2 ( x +x )+2
1 2 1 2
( )
∴2 2x x − 2k+m+3 ( x +x )+2 2m+4k+2 2 =0
1 2 1 2
m2 +1 ( ) 2km
2 2⋅ + 2k+m+3 +2 2m+4k+2 2 =0
k2 −1 k2 −1
( ) ( ) ( )
化简整理得: k+ 2 m2 + 2 2k2 +3k− 2 m+ 2k3+ 2k2 −2k =0
∴
(
m+ 2k
)(
k+ 2
)
m+
(
2k2 +k− 2
)
=0
( )( )
k+ 2 ≠0∴ m+ 2k m+ 2k−1 =0
∴m=− 2k 或m=1− 2k
( )
当m=− 2k,直线l恒过定点 2,0 ;
学科网(北京)股份有限公司( )
当m=1− 2k ,直线l恒过定点A 2,1 ,故舍去.
综上所述,命题得证.
学科网(北京)股份有限公司