文档内容
绝密★启用前
【新结构】江苏省南通市 2024 届新高考适应性调研试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干
净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.数据 的第 百分位数为( )
A. 68,70,80,88,89,90,B96. ,98 15 C. D.
69 70 75 96
2.已知双曲线 的渐近线方程为 ,则双曲线的离心率是
2 2
( ) 2− 2 =1( >0, >0) =±3
A. B. C. D.
10 3 10
3.等差 10 数列 和 的前 项10和分别记为 与 ,1若0 ,则 3 10 ( )
2 8 2+ 9
{ } { } =3 +5 3 =
A. B. C. D.
12 32 16
4.已7知 是两个平面, ,17是两条直线,则下列7命题错 . 误 . 的是 ( 2)
A.如果 , , ,那 么
B.如果 // , ⊂ ,那么 //
C.如果 ⊥ , // ,那么 ⊥
D.如果 // , ⊥ , ,⊥那 么
5.为了更 好⊥的 了 解⊥党 的历 史//, 宣传党的 知⊥ 识,传颂英雄事迹,某校团支部 人组建了“党史宣讲”、“歌
曲演唱”、“诗歌创作”三个小组,每组 人,其中甲不会唱歌,乙不能胜任6诗歌创作,则组建方法有种( )
A. B. 2 C. D.
6.已60知直线 : 72 与直线 30 42平行,则“ ”是“ 平行于 ”
的 1 ( −1) + +3=0 2:( −1) +2 −1=0 =2 1 2
( )
第 页,共 页
1 4
{#{QQABbQaQogAoAABAAQhCAwGaCgIQkBGAACoGABAEsAAAiRNABAA=}#}A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
7.已知 , , ,则 ( )
sin2
∈ (0,2) 2tan =sin +sin 2 tan(2 + +3)=
A. B. C. D.
3 3
8.双−曲线3 的左−,右3 焦点分别为 3,过 作垂直于 轴的3直线交双曲线于 两点,
2 2
: − =4 的内切圆圆心分别 为1, 2 2,则 的面积是 ,
△( ) 1 2,△ 1 2,△ 1 1, 2, 3 △ 1 2 3
A. B. C. D.
二、6多2选−题8:本题共3小题,6共21−8分4。在每小题给8−出4的选2项中,有多项6−符4合题2目要求。全部选对的得6分,
部分选对的得2分,有选错的得0分。
9.关于函数 有下述四个结论,其中错误的是( )
A. 是偶 函( 数)= sin| |+|sin | B. 在区间 单调递增
C. ( ) 在 有 个零点 D. ( ) 的最大 ( 值2为 , )
10. 已( 知) 复[数− ,, ] ,4满足 ,下列说法 正( 确) 的是 ( ) 2
A.若 1 , 2则 | 1|·| 2|≠0 B.
2 2
C.若| 1|= | , 2|则 1 = 2 D. | 1+ 2|≤ | 1|+| 2|
1
1 2 ∈ 2 ∈ | 1 2|=| 1|| 2|
11.已知函数 的定义域为 ,且 , , 为偶函数,则
2 2 3
( )
( ) ( + ) ( − )= ( )− ( ) (1) = 3 (2 +2)
A. B. 为偶函数
C. (0)=0 D. ( )
2023
(3+ )=− (3− ) � =1 ( )= 3
三、填空题:本题共3小题,每小题5分,共15分。
12.定义集合运算: ,集合 ,则集合 所有元
素之和为 ⊙ = | = + , ∈ , ∈ = 0,1 , = 2,3 ⊙
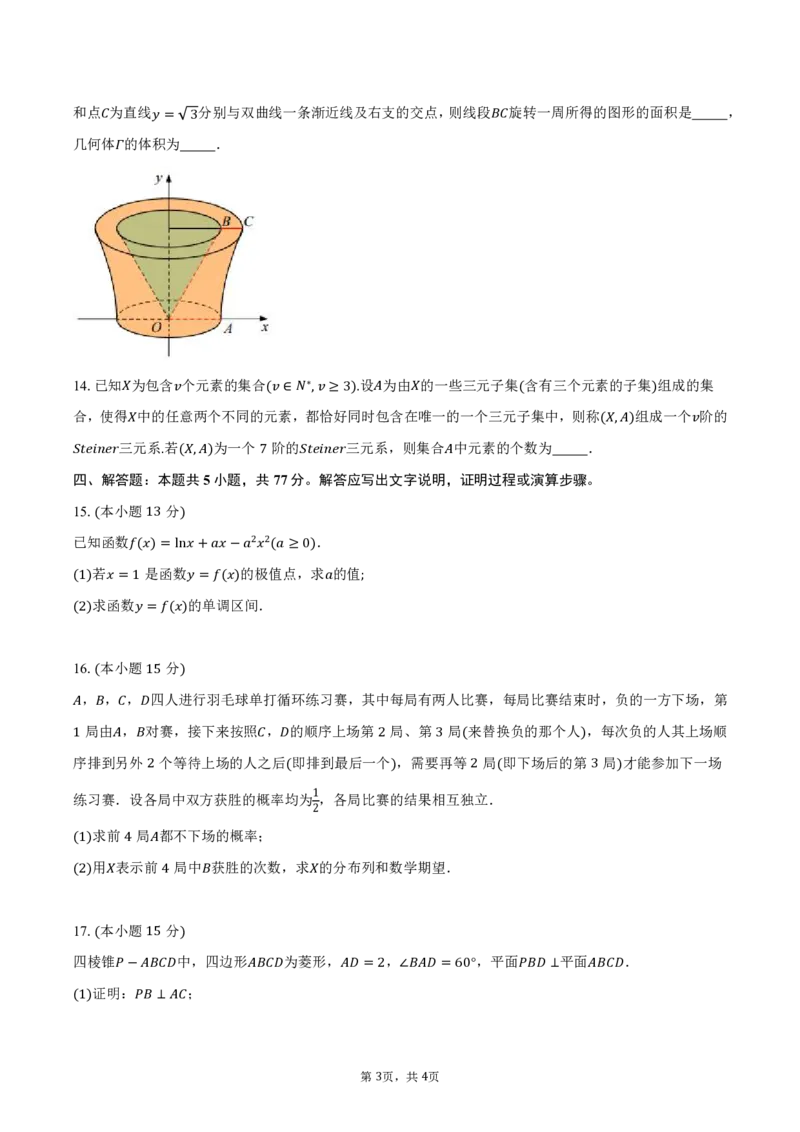
13.早在南北朝时期,祖冲之和他的儿子祖暅在研究几何体的体积时,得到了如下的祖暅原理:幂势既同,
则积不容异。这就是说,夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任意平面所截,
两个截面的面积总相等,那么这两个几何体的体积一定相等,将双曲线 与 所围
2
2
成的平面图形 含边界 绕其虚轴旋转一周得到如图所示的几何体 ,其中 1 线: 段− 3为=双1曲线 的=实0,半 轴=,点3
( )
第 页,共 页
2 4
{#{QQABbQaQogAoAABAAQhCAwGaCgIQkBGAACoGABAEsAAAiRNABAA=}#}和点 为直线 分别与双曲线一条渐近线及右支的交点,则线段 旋转一周所得的图形的面积是 ,
几何体 的体 积=为 3 .
14.已知 为包含 个元素的集合 设 为由 的一些三元子集 含有三个元素的子集 组成的集
∗
合,使得 中的任 意两个不同的元( 素∈, 都, 恰≥好3同).时 包含在 唯一的一个三元子( 集中,则称 组成) 一个 阶的
三 元系若 为一个 阶的 三元系,则集合 中元素的个数为 .( , )
四 、 解 答题:本. 题( 共, 5)小题,共7 77分 。 解 答 应写出文字说明 ,证明过程或演算步骤。
15. 本小题 分
已知(函数 13 ) .
2 2
若 ( 是)函=数ln + −的 极 值( 点≥,0)求 的值
(1)求函 =数1 的=单 调( 区) 间. ;
(2) = ( )
16. 本小题 分
,( , , 1四5人进) 行羽毛球单打循环练习赛,其中每局有两人比赛,每局比赛结束时,负的一方下场,第
局 由 , 对赛,接下来按照 , 的顺序上场第 局、第 局 来替换负的那个人 ,每次负的人其上场顺
1序排到 另外 个等待上场的人之 后 即排到最后一个2 ,需要3再等( 局 即下场后的第) 局 才能参加下一场
2 ( ) 2 ( 3 )
练习赛.设各局中双方获胜的概率均为 ,各局比赛的结果相互独立.
1
求前 局 都不下场的概率; 2
(1)用 表4示前 局中 获胜的次数,求 的分布列和数学期望.
(2) 4
17. 本小题 分
四棱(锥 15 中) ,四边形 为菱形, , ,平面 平面 .
证明 :− ; =2 ∠ =60° ⊥
(1) ⊥
第 页,共 页
3 4
{#{QQABbQaQogAoAABAAQhCAwGaCgIQkBGAACoGABAEsAAAiRNABAA=}#}若 ,且 与平面 成角为 ,点 在棱 上,且 ,求平面 与平面 的夹
1
(角2)的余 弦 =值 . 60° ��� ��=3 ��� �
18. 本小题 分
( 17 )
如图,已知椭圆 : 的左、右项点分别为 , ,左右焦点分别为 , ,离心率为
2 2
2+ 2 =1( > >0) 1 2 1 2
, , 为坐标原点.
3
2 | 1 2|= 2 3
Ⅰ 求椭圆 的方程;
(Ⅱ) 设过点 的直线 , 与椭圆分别交于点 , ,其中 ,求 的面积 的最大值.
( ) (4, ) 1 2 >0 △
19. 本小题 分
( 17 )
已知 1,1 1,2 ⋯ 1, 是 个正整数组成的 行 列的数表,当
2,1 2,2 ⋯ 2, 2
= ( ≥ 2) 1≤ < ≤ ,1 ≤
⋮ ⋮ ⋱ ⋮
时, 记 ,1 ,2 ⋯ , 设 ,若 满足如下两个性质:
∗
① < ≤ ( , , , )=| , − , |+| , −; , |. ∈
② 对 , 任∈意1,2,3;⋯, ( =1,,2存,⋯在, ; =1,2,⋯, ) ,使得 ,则称 为 数表.
∈ 1,2,3,⋯, ∈ 1,2,⋯, , ∈ 1,2,⋯, , =
判断 是否为 数表,并求 的值;
1 2 3
(1) 3 = 2 3 1 3 1,1, 2,2 + 2,2, 3,3
若 数表 3满足1 2 ,求 中各数之和的最小值;
(2)证明 2:对任 4意 数 表 , , +,1,存 +1在=1( =1,2,3; =1,2,3) 4,使得 .
(3) 4 10 1≤ < ≤ 10,1≤ < ≤10 , , , =0
第 页,共 页
4 4
{#{QQABbQaQogAoAABAAQhCAwGaCgIQkBGAACoGABAEsAAAiRNABAA=}#}