江南十校数学详解(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_2024届安徽“江南十校”3月联考数学试题+答案

2024 届安徽省“江南十校”联考 数学试题评分参考 一、单项选择题     1．已知集合A x 2x 1 ,B x1x2 0 ，则AB（ ）         A． x 1x1 B． x0x1 C． x x1 D． x x0 【解析】由2x 1得x0，由1x2 0得1 x1，所以AB {x|x 1} 【答案】C 2．已知复数z满足(12i)z43i，则z=（ ） 2 2 A．2i B．2i C． i D．  i 5 5 43i 105i 【解析】z    2i，所以 z 2i 12i 5 【答案】A 3．已知向量a,b满足ab(1,m)，ab(3,1)．若ab，则实数m（ ） 1 1 A． B． C． 3 D．3 3 3 m1 m1 【解析】由于ab(1,m)，ab(3,1)，所以a (2, ),b(1, ) ，又因为a b ，所以 2 2 m1 m1 1 2  0，解得m ． 2 2 3 【答案】 B． π π 4．已知函数 f(x)3sin(2x)(|| )的图象向右平移 个单位长度后，得到函数g(x)的图象，若g(x)是 2 6 偶函数，则为 A．π B． π C．π D． π 6 6 3 3  【解析】将函数 f(x)3sin(2x)(||0)的图像向右平移 个单位长度后得到g(x)的图象， 6    5 则g(x)sin(2x )，因为g(x)是偶函数，所以20 k ，kZ ，即 k，kZ ， 3 3 2 6   又|| 令k 1，可得 ． ， 2 6 【答案】B． 5．酒驾严重危害交通安全．为了保障交通安全，交通法规定：机动车驾驶人每100ml血液中酒精含量达 到20 ∼ 79mg 为酒后驾车，80mg及以上为醉酒驾车．若某机动车驾驶员饮酒后，其血液中酒精含量上 升到了1.2mg/ml．假设他停止饮酒后，其血液中酒精含量以每小时20%的速度减少，则他能驾驶需要 的时间至少为（精确到0.001．参考数据：lg20.3010，lg30.4771） A．7.963小时 B．8.005小时 C．8.022小时 D．8.105小时 lg6 lg2lg3 【解析】由已知得：1.20.8x 0.2，所以 x  13lg2 13lg2 0.30100.4771 0.7781 即x  8.022，所以x8.022 130.3010 0.0970 【答案】C 11 6．已知函数 f xlnx 在点(1,1)处的切线与曲线yax2 (a1)x2只有一个公共点，则实数a的 x 取值范围为 A．{1,9} B．{0，1,9} C．{1,9} D．{0,1,9} 1 1 【解析】由 f '(x)  得 f '(1)  2 x x2 所以切线方程是 y  2(x1)1 2x3 ①若a0，则曲线为 y x2，显然切线与该曲线只有一个公共点； ②若a0，则2x3ax2 (a1)x2 即 ax2 (a3)x+1=0 由 (a3)2 4a 0，即a2 10a90 得 a1或a9 综上： a0或a1或a9 【答案】B 7．已知圆C:x2  y2 8x120 ，点M(0, 3) ．过原点的直线与圆C 相交于两个不同的点 A,B,则   MAMB 的取值范围为    A． 7 2, 7 2 B． 3，7+2     C． 2 7 4,2 7 4 D． 6，2 7+4     【解析】设AB的中点为点P，则 MAMB 2 MP ，由垂径定理知CPOP，则可得点P的轨迹E 为 以OC为直径的圆（圆C 内部的圆弧）  其方程为E:(x2)2  y2 4(3 x4)，则可得点M(0, 3)到轨迹E 上点P的距离取值范围为 3，7+2，      从而 MAMB 2 MP 的取值范围为 6，2 7+4．  【答案】D 1 8． 已知数列{a }的前n项和为S ,数列{b }的前n项和为T ，且a  S n，a 1，b  ，则 n n n n n1 n 1 n a 1 n 使得T M 恒成立的实数M 的最小值为 n A．1 B．3 C．7 D．2 2 6 【解析】当n1时，a a 12 2 1 当n2时，a S n1 n n1 所以 a a S n(S n1)，即a 2a 1 n1 n n n1 n1 n 所以a 12(a 1) n1 n  1, n1 则{a 1},n2为等比数列，a  n n 32n2 1,n2 即n2时，a 132n2 n 1 1 1 1 7 1 1 7 7 所以T   (1  )    ，得M  n 2 3 2 2n2 6 3 2n2 6 6 【答案】C 2二、多项选择题 9．箱线图是用来表示一组或多组数据分布情况资料的统计图，因形似箱子而得名．在箱线图中（如图1）， 箱体中部的粗实线表示中位数；中间箱体的上下底，分别是数据的上四分位数（75%分位数）和下四分 位数（25%分位数）；整个箱体的高度为四分位距；位于最下面和最上面的实横线分别表示最小值和最 大值（有时候箱子外部会有一些点，它们是数据中的异常值）．图2为某地区2023年5月和6月的空 气质量指数(AQI)箱线图．AQI值越小，空气质量越好；AQI值超过200，说明污染严重．则 (第9题图1) (第9题图2) A．该地区2023年5月有严重污染天气． B．该地区2023年6月的AQI值比5月的AQI值集中． C．该地区2023年5月的AQI值比6月的AQI值集中． D．从整体上看，该地区2023年5月的空气质量略好于6月． 【解析】对于A选项可以从图2所示中5月份有AQI值超过200的异常值得到判断（也可以通过异常值 结合观察5月份的平均值高于中位数辅助判断）；对于B，C选项，图2中5月份的箱体高度比6月份的 箱体高度小，说明5月的AQI值比6月的AQI值集中；对于D选项，虽然5月有严重污染天气，但从图 2所示中5月份箱体整体上比6月份箱体偏下且箱体高度小，AQI值整体集中于较小值，说明从整体上看， 该地区2023年5月的空气质量略好于6月． 【答案】ACD 10．已知抛物线E:y2 2px的焦点为F ，从点F 发出的光线经过抛物线上的点P（原点除外）反射，则 反射光线平行于x轴． 经过点F 且垂直于x轴的直线交抛物线E 于B,C两点，经过点P且垂直于x 轴的直线交x轴于Q；抛物线E在点P处的切线l与x,y轴分别交于点M,N ，则下列说法成立的是 A． PQ 2  BF QF B． PQ 2  BC OQ C． PF  MF D． FN l p p 【解析】对于A，B选项，设点P(x,y)，而 PQ  2px ，而 BF  p,QF  x ，BF QF  p x ， 2 2 则A选项错误， 又 BC 2p,OQ  x，则B选项正确；对于C选项，如下图所示，过点P作x轴的平行 线RH ，与抛物线E 的准线KH 交于点H ，又题意所给抛物线的光学性质可得SPRMPF ，又 SPRPMF ，所以MPF PMF ，从而 PF  MF ；对于 D 选项，因为SPRHPM ，所以 MPF HPM ，即PM 为HPF 的角平分线，又由抛物线定义知PH  PF ，结合 PF  MF ，可得 菱形MFPH ，而 y轴经过线段FH 中点，从而PM 与 y轴的交点即为点N ，所以FN l． 3【答案】BCD 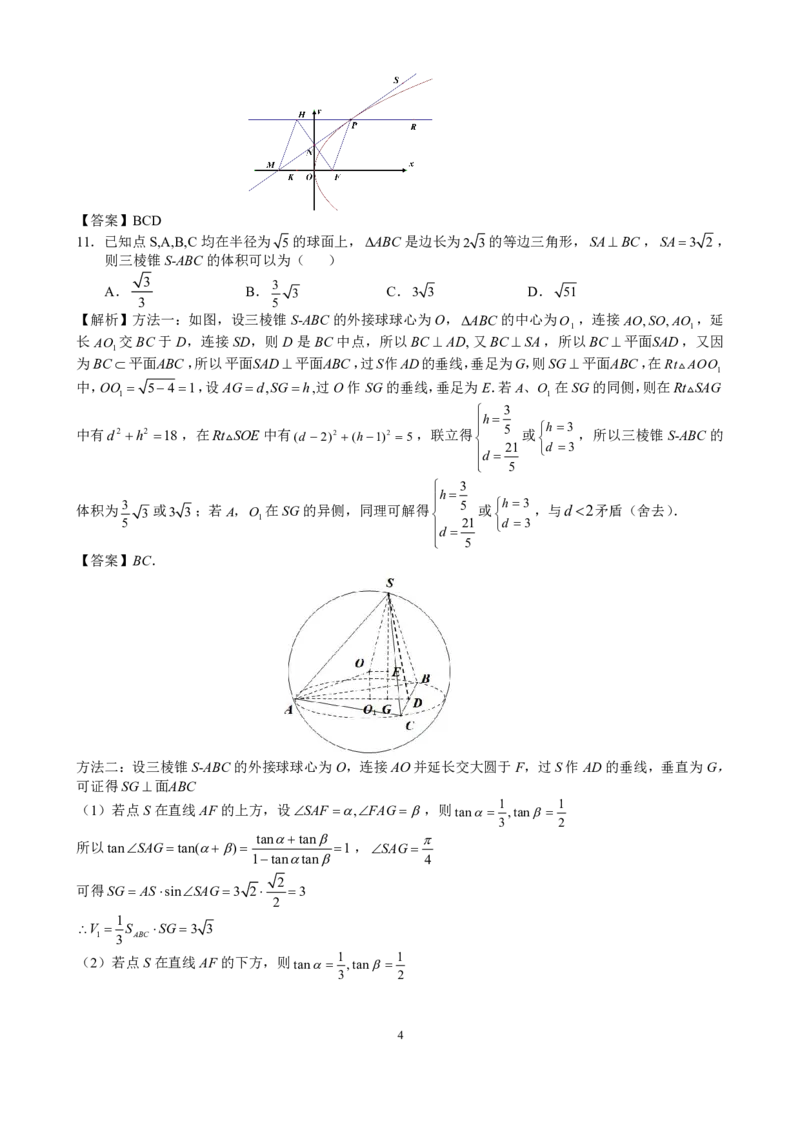11．已知点S,A,B,C均在半径为 5的球面上，ABC是边长为2 3的等边三角形，SABC，SA3 2 ， 则三棱锥S-ABC的体积可以为（ ） A． 3 B．3 3 C．3 3 D． 51 3 5 【解析】方法一：如图，设三棱锥S-ABC的外接球球心为O，ABC的中心为O ，连接AO,SO,AO ，延 1 1 长AO 交BC于D，连接SD，则D是BC中点，所以BC  AD,又BCSA，所以BC平面SAD，又因 1 为BC平面ABC，所以平面SAD平面ABC，过S作AD的垂线，垂足为G，则SG平面ABC，在RtAOO 1 中，OO  54 1，设AGd,SGh,过O作SG的垂线，垂足为E．若A、O 在SG的同侧，则在RtSAG 1 1  3 h 中有d2 h2 18，在RtSOE中有(d 2)2 (h1)2 5，联立得    5 或   h3 ，所以三棱锥S-ABC的  d  21 d 3  5  3 h 体积为3 3 或3 3；若A，O 在SG的异侧，同理可解得    5 或   h3 ，与d2矛盾（舍去）． 5 1  d  21 d 3  5 【答案】BC． 方法二：设三棱锥S-ABC的外接球球心为O，连接AO并延长交大圆于F，过S作AD的垂线，垂直为G， 可证得SG面ABC （1）若点S在直线AF的上方，设SAF ,FAG，则 tan 1 ,tan 1 3 2 tantan  所以tanSAGtan() 1 ，SAG 1tantan 4 2 可得SG ASsinSAG3 2 3 2 1 V  S SG3 3 1 3 ABC （2）若点S在直线AF的下方，则 tan 1 ,tan 1 3 2 4tantan 1 2 所以tanSAGtan()  ，sinSAG 1tantan 7 10 2 3 可得SG ASsinSAG3 2  10 5 1 3 3 V  S SG  ，故选BC． 2 3 ABC 5 【答案】BC． 三、填空题 12．从0,2,4,6中任意取1个数字，从1,3,5中任意选2个数字，得到没有重复数字的三位数．在所组成的 三位数中任选一个，则该数是偶数的概率为 ． 【解析】若0在，则三位数有 C1A2 12；若0不在，则三位数有 C1C2A3 54．所以没有重复数字的 2 3 3 3 3 三位数有66个，其中偶数的个数是C1A2 24个，所以在所组成的三位数中任选一个，是偶数的概率是 4 3 24 4  66 11 4 【答案】 ． 11 13．若函数 f  x2 为偶函数，y  g  x1 5是奇函数，且 f  2x g  x 2，则 f  2023  =______． 【解析】由 f  x2 为偶函数，得 f  2x  f(2x)， 由 y g  x1 5是奇函数，得g  1x 5g(1x)5，即g(2x) g(x)10 由 f  2x g  x 2，得 f  x +g  2x 2 相加得： f (2x) f (x) 6() 用2x代换x得 f (2 x) f (x) 6 从而 f (4 x) f (x2) 6 故 f  x4  f(x) 所以4是y f  x 的一个周期 故 f  2023  =f(3) f(1)结合()式得 f (3)  f (1)  3 【答案】3． x2 y2 14．在平面直角坐标系xOy中，过双曲线E:  1(a0，b0)的右焦点F的直线在第一、第二象限 a2 b2 2 交E的两渐近线分别于M,N 两点,且OM MN．若 OM  MN  ON  a ，则双曲线E的离心率 3 为 ． b 【解析】如图，设FOM ,MON 2，因为OM MN，易知 FM b，tan ，所以 OM a； a 2 1 4 又 OM  MN  ON  a ，所以 MN  ON  a，在直角OMN中，利用勾股定理可得 MN  a， 3 3 3 4 1 b 1 所以tan2 ，求得tan （负值舍去），也即tan  2，所以可得离心率为 5． 3 2 a tan 【答案】 5． 5四、解答题 15．已知a,b,c分别是ABC三个内角A,B,C 的对边，且 3csinAacosC bc． (1)求A; (2)若BC2，将射线BA和CA分别绕点B,C 顺时针旋转15,30，旋转后相交于点D(如图所示)，且 DBC30，求AD． 15. 【解析】（1）因为 3csinAacosC bc 所以 3sinCsinAsinAcosC sinBsinC 又因为sinBsin(AC)sinAcosCcosAsinC 所以 3sinCsinAcosAsinCsinC ······································································（3分）  1 由于sinC0，所以 3sinAcosA1，即sin(A ) ， 6 2   5    又  A  ，则A  ，因此A ．······················································ （6分） 6 6 6 6 6 3 BC 2 6 （2）在ABC中，由正弦定理得AC  sinABC  sinBAC 3 在BDC中，由于BDC 45 BC 由正弦定理得CD sinDBC 2．·························································（10分） sinBDC 于是，在ACD中，由余弦定理得： 8 2 6 3 6 AD  AC2CD22ACCDcosACD  22  2  ················ （13分） 3 3 2 3 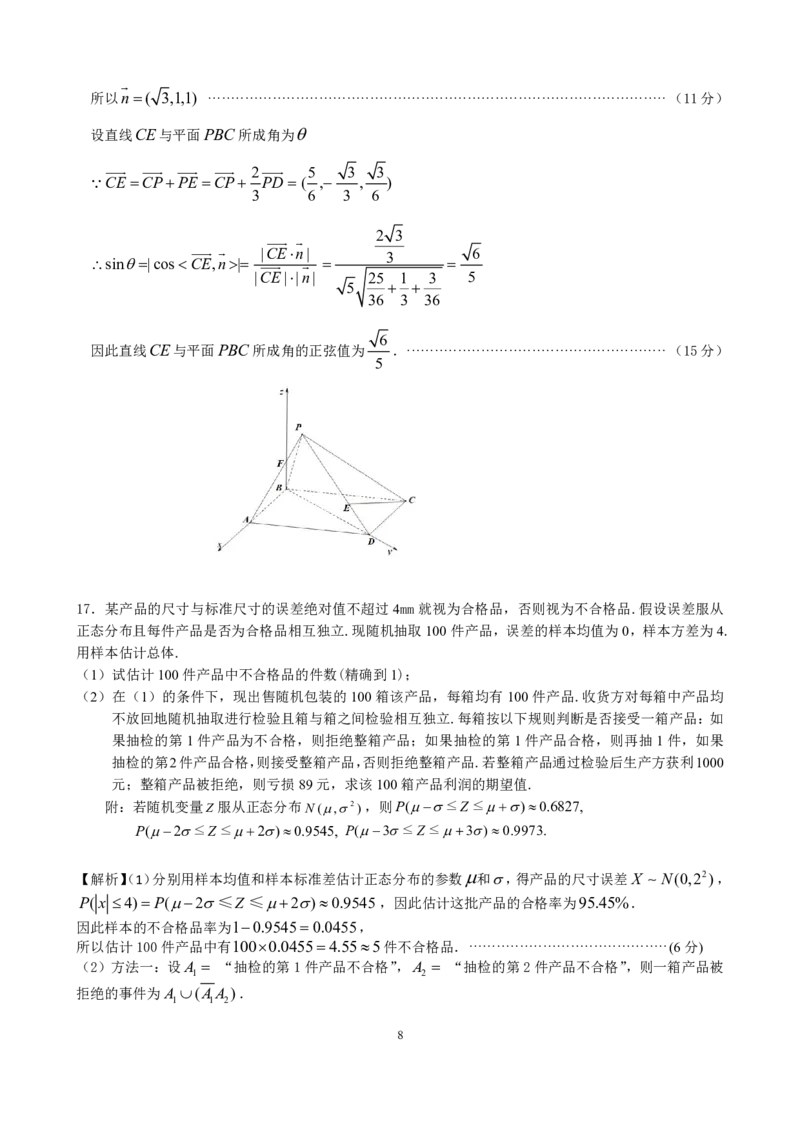616．如图，在四棱锥PABCD中，底面ABCD为平行四边形，PB AB1, ADPD2,BAD60. （1）求证：平面PAB 平面ABCD； （2）若二面角PBD A的大小为120，点E 在棱PD上，且PE 2ED，求直线CE与平面PBC所成 角的正弦值. 【解析】（1）证明：由余弦定理得 BD 12 22 212cos60  3 所以AD2  AB2 BD2，PD2 PB2 BD2 因此AB BD，PB BD 又因为ABPB  B,AB,PB平面PAB 所以BD面PAB 又因为BD平面ABCD 故平面PAB平面ABCD ·····················································································（6分） （2）由于AB BD，PB BD 所以二面角PBDA的平面角为PBA，即PBA 1200 ·······································（7分） 在平面PAB内过点B作AB的垂线，交AP于F 由平面PAB平面ABCD， 得BF 平面ABCD   以B为坐标原点，BA,BD，BF 为x,y,z轴正方向 建立如图所示的空间直角坐标系Bxyz 1 3 则B(0,0,0),D(0, 3,0),C(1, 3,0)，P( ,0, )····················································（9分） 2 2    1 3 设平面PBC的法向量为n(x,y,z)，由于BC (1, 3,0), BP( ,0, ) 2 2   x 3y 0  nBC 0  则  ，即 1 3 ，令x 3，则 y  z 1 nBP 0  x z  0  2 2 7 所以n( 3,1,1) ···································································································（11分） 设直线CE与平面PBC所成角为     2 5 3 3 CE CPPE CP PD  ( , , ) 3 6 3 6 2 3     |CEn| 3 6 sin|cosCE,n|     |CE||n| 25 1 3 5 5   36 3 36 6 因此直线CE与平面PBC所成角的正弦值为 ．························································（15分） 5 17．某产品的尺寸与标准尺寸的误差绝对值不超过4mm就视为合格品，否则视为不合格品.假设误差服从 正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品，误差的样本均值为0，样本方差为4. 用样本估计总体. （1）试估计100件产品中不合格品的件数(精确到1)； （2）在（1）的条件下，现出售随机包装的100箱该产品，每箱均有100件产品.收货方对每箱中产品均 不放回地随机抽取进行检验且箱与箱之间检验相互独立.每箱按以下规则判断是否接受一箱产品：如 果抽检的第1件产品为不合格，则拒绝整箱产品；如果抽检的第1件产品合格，则再抽1件，如果 抽检的第2件产品合格，则接受整箱产品，否则拒绝整箱产品.若整箱产品通过检验后生产方获利1000 元；整箱产品被拒绝，则亏损89元，求该100箱产品利润的期望值. 附：若随机变量Z 服从正态分布N(,2)，则P(≤Z ≤)0.6827, P(2≤Z ≤2)0.9545, P(3≤Z≤3)0.9973. 【解析】（1）分别用样本均值和样本标准差估计正态分布的参数  和，得产品的尺寸误差X  N(0,22)， P(x 4)P(2≤Z ≤2)0.9545，因此估计这批产品的合格率为95.45%． 因此样本的不合格品率为10.95450.0455， 所以估计100件产品中有1000.04554.555件不合格品．···········································(6分) （2）方法一：设A  “抽检的第1件产品不合格”，A  “抽检的第2件产品不合格”，则一箱产品被 1 2 拒绝的事件为A (AA )． 1 1 2 8因此P(A (AA )) P(A)P(AA ) P(A)P(A)P(A A) 1 1 2 1 1 2 1 1 2 1 5 95 5 97     ．·····················································································(10分) 100 100 99 990 893 设100箱产品通过检验的箱数为Z ，则Z  B(100, )． 990 所以100箱利润W 1000Z (89)(100Z)1089Z 8900 893 因此平均利润E(W)E(1089Z 8900)1089E(Z)89001089100 8900 990 89330（元）． ················································································· (15分) C2 97 方法二：记一个整箱产品被拒绝为事件A，则P(A)1 95  ··································· (10分) C2 990 100 97 97 893 设整箱产品的利润为随机变量，则P(89) ，P(1000)1  990 990 990 97 893 884367 所以E()89 1000  990 990 990 设100箱该产品的利润为随机变量X，则X 100 所以E(X)E(100)100E()89330 （元）． ··························································(15分) 18．已知矩形ABCD中，AB2 6,BC 2 2 ，E,F,G,H 分别是矩形四条边的中点，以矩形中心O为 原点，HF 所在直线为x轴，EG所在直线为 y 轴，如图建立平面直角坐标系．直线HF,BC上的动     点R,S 满足OROF,CS CF(R)． (1)求直线ER与直线GS交点P的轨迹方程； 6 (2) 当  时，过点R的直线m（与x 轴不重合）和点P的轨迹交于M,N 两点，过点N 作直线 3 l:x3的垂线，垂足为点Q．设直线MQ与x轴交于点K ，求KMN 面积的最大值． 【解析】（1）设点P(x,y)，R(x ,0)，S( 6,y ) R S   由OR OF得x  6，即R( 6,0) R   由CS CF 得y  2(1)，即S( 6, 2(1)) S 2 当 0时，直线ER: y  x 2 ① 6 9 2 直线GS :y  x 2 ② 6 1 由①②消去参数得(y 2)(y 2)  x2 3 x2 y2 即  1(x 0)； 6 2 当0时，得交点P(0, 2)； x2 y2 综上：直线ER与直线GS交点P的轨迹方程：  1(不含点(0, 2))···························(6分) 6 2 6 （2）当  时，点R(2,0)，过点R的直线m可设为x ty2(t   2) 3 x2 y2 代入  1得(ty2)2 3y2  6 6 2 即(t2 3)y2 4ty20 设M(x ,y ),N(x ,y ) 1 1 1 2 4t 2 则y  y  ,y y   1 2 t2 3 1 2 t2 3 由题得Q(3,y ) 2 y  y 则直线MQ:y y  1 2 (x3) 2 x 3 1 所以令y0 y (x 3) y x 3y 得x  2 1 3 2 1 1 ·················································································(8分) k y  y y  y 1 2 1 2 又因为x ty 2,2ty y  (y  y )，代入上式得： 1 1 1 2 1 2 1 (y  y )2y 3y y (ty 2)3y ty y 2y 3y 2 1 2 2 1 x  2 1 1  1 2 2 1  k y y y y y y 1 2 1 2 1 2 5 5  y  y 2 1 2 2 5   y y 2 1 2 5 所以直线MQ过定点K( ,0)·······················································································(12分) 2 1 1 5 1 由于S  KR y y  2 y y  y y KMN 2 1 2 2 2 1 2 4 1 2 4t 8 t2 1 而 y y  (y  y )24y y  ( )2 2 6 ·····································(14分) 1 2 1 2 1 2 t2 3 t2 3 (t2 3)2 令nt2 1(n1) n 1 y  y 2 6 2 6 1 2 n2 4n4 4 n 4 n 101 2 6  3 2 44 当且仅当n2，也即t 1等号成立 3 此时S  KMN 4 3 所以KMN 面积的最大值为 ····················································································(17分) 4 19．已知函数 f (x)  (x  a)ex  x,aR ， f(x)是 f(x)的导函数. （1）证明： f(x)在(,)上有唯一零点x ； 0 1 （2）设函数g(x)(x2 ax1)ex ( x2 x1). 2 e4  ①当a  , 时，求函数g(x)的单调区间；  2  e4 ②当a(, )时，讨论函数g(x)零点的个数. 2 【解析】（1） f(x)=(xa1)ex 1 1 由 f(x)0得，xa1 0 ex 1 1 令h(x)xa1 ，则h(x)1 0 ex ex 所以h(x)为R上的增函数 1 又h(a1) 0 ea1 1 若a0，由于a1a1且h(a1)2 0 ea1 1 1 若a0，由于aa1且h(a)12a (1 )2a0 ea ea 综上：存在唯一零点x (,)，使得h(x )0 0 0 即 f(x)在(,)上有唯一零点x ．···································································(5分) 0 （2）g(x)(x1)(xa1)ex (x1) 1 (x1)(xa1 )ex ex 1 ①由（1）知，h(x) xa1 有唯一零点x 且为增函数，所以g(x)0的根为1,x ex 0 0． e4 3e4 又h(1)aee  0，则x 1 2 2 0 所以由g(x)0得x1或xx ；由g(x)0得1 x x 0 0 所以函数g(x)的递增区间是(,1),(x ,)；递减区间是(1,x )······································ (9分) 0 0 ②由g(0)0得0是函数g(x)的一个零点． e4 （ⅰ）若ea ，由①同理可得x 1 2 0 11当x(,1)时，g(x)0，则g(x)单调递增 当x(1,x )时，g(x)0，则g(x)单调递减 0 当x(x ,)时，g(x)0，则g(x)单调递增 0 2a4e 又因为g(x) =g(1)  0 极大值 2e 所以g(x)仅有一个零点0； （ⅱ）若ae，则h(1)1e1e0，即x 1 0 则g(x)0，所以x(,)时，g(x)单调递增. 所以g(x)仅有一个零点0 ； （ⅲ）若ae，则h(1)ae0，所以x 1 0 当x(,x )时，g(x)0，则g(x)单调递增 0 当x(x ,1)时，g(x)0，则g(x)单调递减 0 当x(1,)时，g(x)0，则g(x)单调递增 1 1 所以g(x) =g(x )(x2 ax 1)ex 0 ( x2 x 1) (x2 ex 1)ex 0 ( x2 x 1) 极大值 0 0 0 2 0 0 0 0 2 0 0 1 1 1 因为x 1，所以 x2 x 1 (1)2 (1)1 0 0 2 0 0 2 2 1 当x2 ex 10时，(x2 ex 1)ex 0 ( x2 x 1)0 0 0 0 0 2 0 0 1 1 1 当x2 ex 10时，(x2 ex 1)ex 0 ( x2 x 1)(x2 ex 1) ( x2 x 1) 0 0 0 0 2 0 0 0 0 e 2 0 0 1 1 e 1  (x2ex 1) x2x 1( 1)x  0 2 0 0 2 0 0 2 0 2 所以g(x)仅有一个零点0． e4 综上：当a(, )时，函数g(x)仅有一个零点0．·····················································(17分) 2 12