文档内容
高三第一次调研考试
数学试题
命题人:分宜中学 谢平 新钢中学 邹进辉 审题人:刘勇刚
说明:1.本卷共有四个大题,22个小题,全卷满分150分,考试时间120分钟.
2.本卷分为试题卷和答题卷,答案要求写在答题卷上,在试题卷上作答不给分.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知函数 的定义域为集合A,集合 ,则 ( )
A. B. C. D.
2.已知复数z满足: ,则 ( )
A.1 B. C. D.5
3.在 中,“ ”是“ 为直角三角形”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.为庆祝我国第39个教师节,某校举办教师联谊会,甲、乙两名数学老师组成“几何队”参加“成语猜猜
猜”比赛,每轮比赛由甲、乙两人各猜一个成语,已知甲每轮猜对的概率为 ,乙每轮猜对的概率为 .在
每轮比赛中,甲和乙猜对与否互不影响,则“几何队”在一轮比赛中至少猜对一个成语的概率为( )
A. B. C. D.
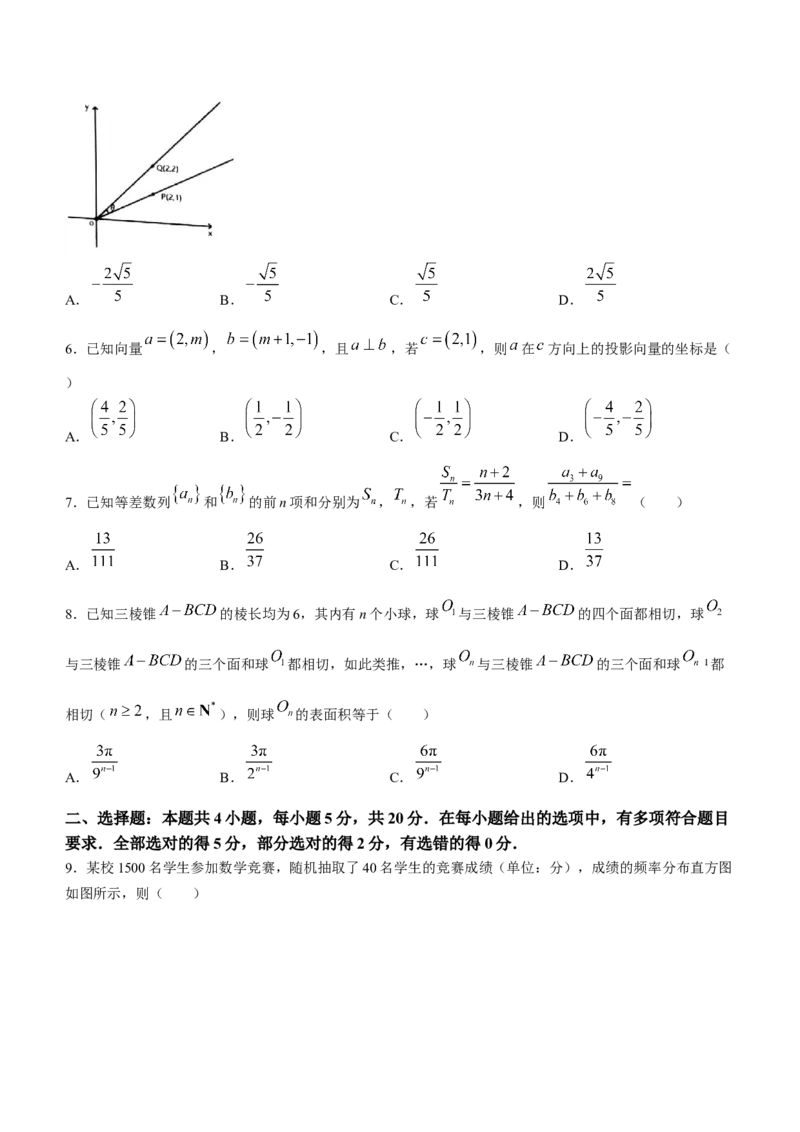
5.如图, ( )
学科网(北京)股份有限公司A. B. C. D.
6.已知向量 , ,且 ,若 ,则 在 方向上的投影向量的坐标是(
)
A. B. C. D.
7.已知等差数列 和 的前n项和分别为 , ,若 ,则 ( )
A. B. C. D.
8.已知三棱锥 的棱长均为6,其内有n个小球,球 与三棱锥 的四个面都相切,球
与三棱锥 的三个面和球 都相切,如此类推,…,球 与三棱锥 的三个面和球 都
相切( ,且 ),则球 的表面积等于( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
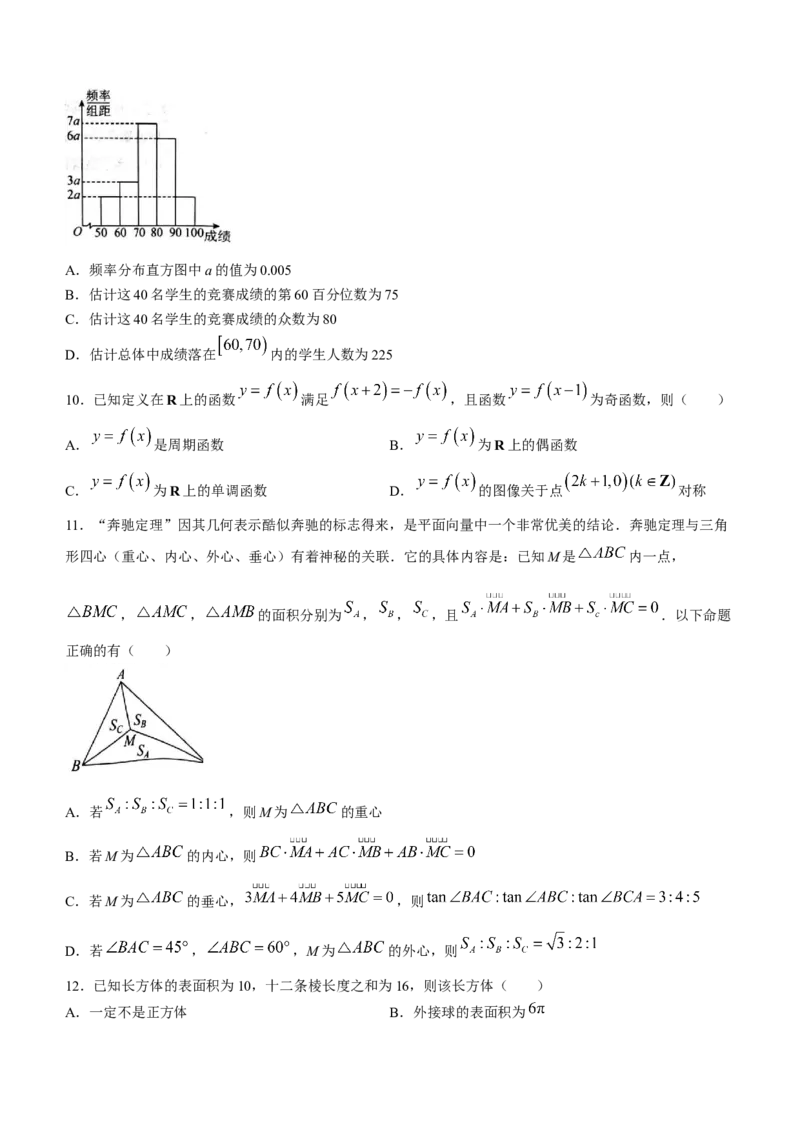
9.某校1500名学生参加数学竞赛,随机抽取了40名学生的竞赛成绩(单位:分),成绩的频率分布直方图
如图所示,则( )
学科网(北京)股份有限公司A.频率分布直方图中a的值为0.005
B.估计这40名学生的竞赛成绩的第60百分位数为75
C.估计这40名学生的竞赛成绩的众数为80
D.估计总体中成绩落在 内的学生人数为225
10.已知定义在R上的函数 满足 ,且函数 为奇函数,则( )
A. 是周期函数 B. 为R上的偶函数
C. 为R上的单调函数 D. 的图像关于点 对称
11.“奔驰定理”因其几何表示酷似奔驰的标志得来,是平面向量中一个非常优美的结论.奔驰定理与三角
形四心(重心、内心、外心、垂心)有着神秘的关联.它的具体内容是:已知M是 内一点,
, , 的面积分别为 , , ,且 .以下命题
正确的有( )
A.若 ,则M为 的重心
B.若M为 的内心,则
C.若M为 的垂心, ,则
D.若 , ,M为 的外心,则
12.已知长方体的表面积为10,十二条棱长度之和为16,则该长方体( )
A.一定不是正方体 B.外接球的表面积为
学科网(北京)股份有限公司C.长、宽、高的值均属于区间 D.体积的取值范围为
三、填空题:本题共4小题,每小题5分,共20分.
13.若直线 与圆 相切,则实数 ______.
14.已知正实数x,y满足方程 ,则 的最小值为______.
15.杭州第19届亚运会于2023年9月23日至10月8日举办,杭州亚运会竞赛项目设置为40个大项,61个
分项,481个小项,并增设电子竞技、霹雳舞两个竞赛项目.现有甲、乙、丙、丁、戊5名志愿者到乒乓球、
电子竞技、霹雳舞三个项目志愿服务,其中每个项目至少一名志愿者,甲必须在霹雳舞项目,则不同的志愿
服务方案共有______种.
16.已知双曲线 的左、右焦点分别为 , ,过点 作倾斜角为 的直线l
与C的左、右两支分别交于点P,Q,若 ,则C的离心率为______.
四、解答题:(本大题共6小题,17题10分,18~22题各12分,共70分.解答须写出文字说
明、证明过程和演算步骤)
17.已知 的内角A,B,C的对边分别为a,b,c,若 ,且 .
(1)求A;
(2)若D为 的中点,且 ,求 的面积.
18.如图, 与 都是边长为2的正三角形,平面 平面 , 平面 且
.
(1)证明: 平面 .
学科网(北京)股份有限公司(2)求平面 与平面 的夹角的大小.
19.在平面直角坐标系 中,动点P到点 的距离等于点P到直线 的距离.
(1)求动点P的轨迹方程;
(2)记动点P的轨迹为曲线C,过点F的直线l与曲线C交于A,B两点, ,直线 的斜率为
,直线 的斜率为 .证明: 为定值.
20.魔方,又叫鲁比可方块,最早是由匈牙利布达佩斯建筑学院厄尔诺·鲁比克教授于1974年发明的机械益
智玩具.魔方拥有竞速、盲拧、单拧等多种玩法,风靡程度经久未衰,每年都会举办大小赛事,是最受欢迎
的智力游戏之一.通常意义下的魔方,是指狭义的三阶魔方.三阶魔方形状通常是正方体,由有弹性的硬塑
料制成.常规竞速玩法是将魔方打乱,然后在最短的时间内复原.广义的魔方,指各类可以通过转动打乱和
复原的几何体.魔方与华容道、法国的单身贵族(独立钻石棋)并称为智力游戏界的三大不可思议,在
2018WCA世界魔方芜湖公开赛上,杜宇生以3.47秒的成绩打破了三阶魔方复原的世界纪录,勇夺世界魔方
运动的冠军,并成为世界上第一个三阶魔方速拧进入4秒的选手.
(1)小王和小吴同学比赛三阶魔方,已知小王每局比赛获胜的概率均为 ,小吴每局比赛获胜的概率均为
,若采用三局两胜制,两人共进行了X局比赛,求X的分布列和数学期望;
(2)小王和小吴同学比赛四阶魔方,首局比赛小吴获胜的概率为0.5,若小王本局胜利,则他赢得下一局比
赛的概率为0.6,若小王本局失败,则他赢得下一局比赛的概率为0.5,为了赢得比赛,小王应选择“五局三
胜制”还是“三局两胜制”?
21.已知等差数列 与等比数列 满足 , , ,且 既是 和 的等差中
项,又是其等比中项.
(1)求数列 和 的通项公式;
(2)记 ,其中 ,求数列 的前2n项和 ;
(3)记 ,其前n项和为 ,若 对 恒成立,求 的最小值.
22.已知函数 , 且 .
学科网(北京)股份有限公司(1)当 时,求曲线 在 处的切线方程;
(2)若 ,且 存在三个零点 , , .
(i)求实数a的取值范围;
(ii)设 ,求证: .
高三数学试题卷参考答案
一、单选题(每小题5分,共40分)
题号 1 2 3 4 5 6 7 8
答案 D A D B C A C D
二、多选题(每小题5分,共20分,全部选对的得5分,部分选对的得2分,有选错的得0
分)
题号 9 10 11 12
答案 AD ABD ABC ABD
三、填空题(每题5分,共20分)
13.7或 14. 15.50 16.
四、解答题(共70分)
17.(1)因为 ,所以 ,
由正弦定理得 ,
化简得 .
因为 , ,所以 .
因为 ,所以 .
(2)因为D为 的中点,所以中所 ,
等式两边平方得 ,
即 ①.
学科网(北京)股份有限公司在 中,由余弦定理得 ②,
联立①②解得 ,所以 .
18.(1)取 中点F,连接 ,
, 都是边长为2的正三角形,
, , ,
又 , 面 , 面 ,
面 ,
又平面 平面 ,
面 且
又 面 且
, , ,
是正方形,
又 , 平面 , 平面 ,
平面
(2)由(1)知 , , 两两垂直,如图建立空间直角坐标系
学科网(北京)股份有限公司由于x轴垂直面
平面 的法向量为
又 , ,
,
设平面 的法向量 ,
则 ,
令 ,则 , ,所以
平面 与平面 的夹角为
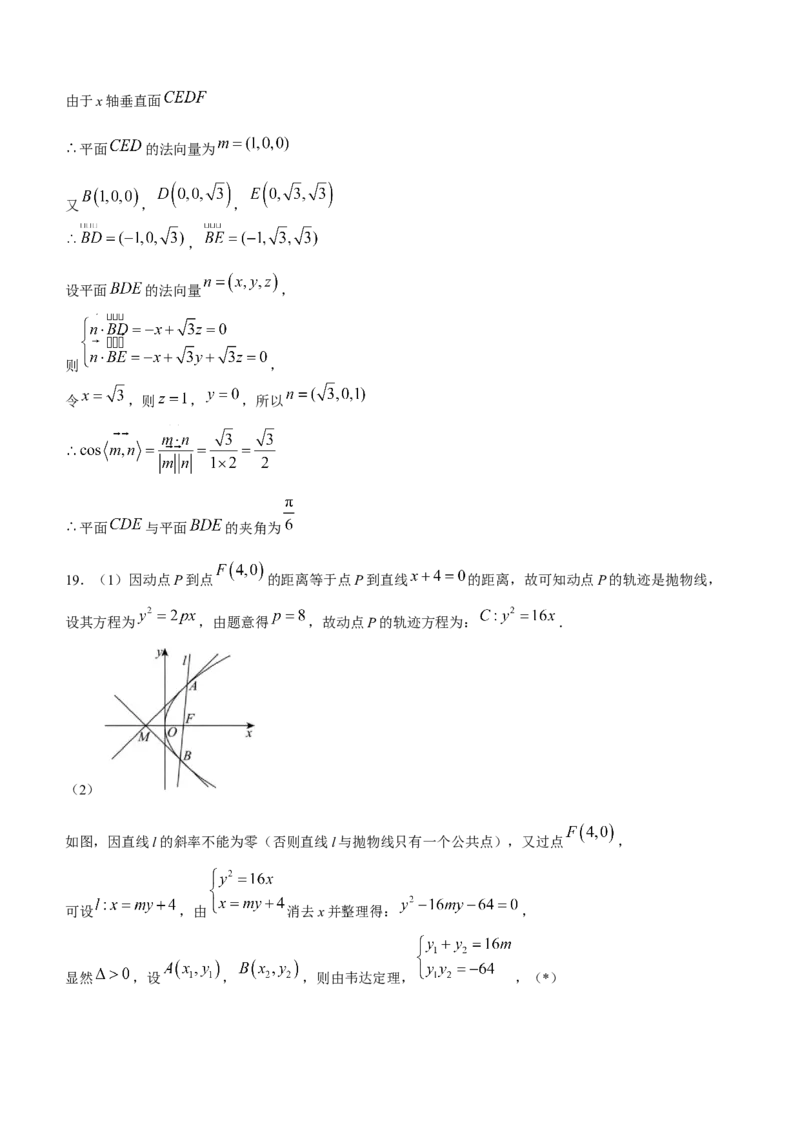
19.(1)因动点P到点 的距离等于点P到直线 的距离,故可知动点P的轨迹是抛物线,
设其方程为 ,由题意得 ,故动点P的轨迹方程为: .
(2)
如图,因直线l的斜率不能为零(否则直线l与抛物线只有一个公共点),又过点 ,
可设 ,由 消去x并整理得: ,
显然 ,设 , ,则由韦达定理, ,(*)
学科网(北京)股份有限公司则 ,
将(*)代入得: ,
故 为定值0.
20.(1)因为采用三局两胜制,所以X的可能取值为2,3,
表示小王或小吴连胜两局; 表示小王与小吴前两局一胜一负;
所以 , ,
所以X的分布列为:
X 2 3
P
则X的数学期望为 .
(2)若小王选择“三局两胜制”,
则小王获胜的情况为:胜胜;胜负胜;负胜胜;
则小王获胜的概率为 ;
若小王选择“五局三胜制”,
则小王获胜的情况为:胜胜胜;胜胜负胜;胜负胜胜;负胜胜胜;胜胜负负胜;胜负胜负胜;胜负负胜胜;
负负胜胜胜;负胜负胜胜;负胜胜负胜;
则小王获胜的概率为
,
因为 ,
所以小王应选择“五局三胜制”.
21.(1)设等差数列 的公差为d,等比数列 的公比为q,
, ,所以 ,解得 , ,
既是 和 的等差中项,又是其等比中项,
学科网(北京)股份有限公司得 , ,
解得 ,即 ,
所以 , .
(2) ,
.
又
,
①
②
①减②得:
,
.
(3) , , ,则 是首项为 公比为 的等比数列,
, ,
学科网(北京)股份有限公司令 , ,
当n为奇数时, ,且 递减,
可得 的最大值为 ,
当n为偶数时, ,且 递增,
可得 的最小值为 ,
所以 的最小值为 ,最大值为 ,因为 ,对 恒成立,
所以 ,所以 ,所以 的最小值为 .
22.(1)当 时 ,则 ,
又 ,所以 ,
所以曲线 在 处的切线方程为 ,即 .
(2)(i)因为 , 且 存在三个零点 , , ,
所以 有3个根,
当 时, , , ,
所以 在 上是单调递增,由零点存在定理,方程必有一个负根,
当 , ,即 有两个根,
学科网(北京)股份有限公司令 ,可转化为 与 有两个交点,
,
可得 时 ,即 在 单调递增,
可得 时 ,即 在 单调递减,
其中 ,当 , ,
所以可得 ,解得 .
(ii)因为 , 且 存在三个零点 , , ,
设 , , , ,易知其中 , ,
因为 ,所以 ,所以 , , ,
故可知 ①;
由(i)可知 与 有两个交点 ,
当 , 是单调递增,所以 , , ,所以 ②;
即 , ,
若 ,则 ,
若 ,构造函数 , ,
则
,
学科网(北京)股份有限公司设 ,
则 ,
因为 ,
又因为 , , , ,
所以 ③;
因为
,
又因为 , , , ,
所以 , ; , ,
即得 ④;
由③④可知 , 在 上单调递增,
又 可得 ,
,可知 与 同号,所以 ,
所以 在 上单调递增,所以 ,
所以 ,即 ,
又由(i)可知 ,
所以 , , ,
, , 是单调递增,
学科网(北京)股份有限公司所以 , ⑤,
由①②⑤可知 .
学科网(北京)股份有限公司