河南省TOP二十名校2024届高三下学期5月联考猜题（一）数学试卷(1)_2024年5月_025月合集_2024届河南省TOP20名校高三5月联考猜题（一）

绝密★启用前 2024 届高三年级 TOP 二十名校猜题一 数学 全卷满分 150分，考试时间 120分钟 注意事项： 1.答卷前，考生务必将自己的姓名，准考证号填写在答题卡上，并将条形码粘贴在答题卡上 的指定位置. 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改 动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本 试卷上无效. 3.考试结束后，将本试卷和答题卡一并收回. 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1.在复平面内，复数z 25i12i 对应的点位于（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.设集合A1,2a1,B3,a1,3a2 ，若A B，则a （ ） A.-2 B.-1 C.1 D.3 3.设角的顶点与直角坐标系的原点重合，始边与x轴非负半轴重合，则 π 3π “2kπ 2kπ kZ ”是“cos„ 0”的（ ） 2 2 A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分又不必要条件 π 4.将函数y 3sin3x 的图象向右平移 个单位长度，得到的函数图象关于y轴对称，则的最小值 9 为（ ） π 7π 11π 5π A. B. C. D. 6 18 18 6 5.在某电路上有M､N 两个独立工作的元件，每次通电后，需要更换M 元件的概率为0.3，需要更换N 元 件的概率为0.2，则在某次通电后M､N 有且只有一个需要更换的条件下，M 需要更换的概率是（ ） 12 15 2 3 A. B. C. D. 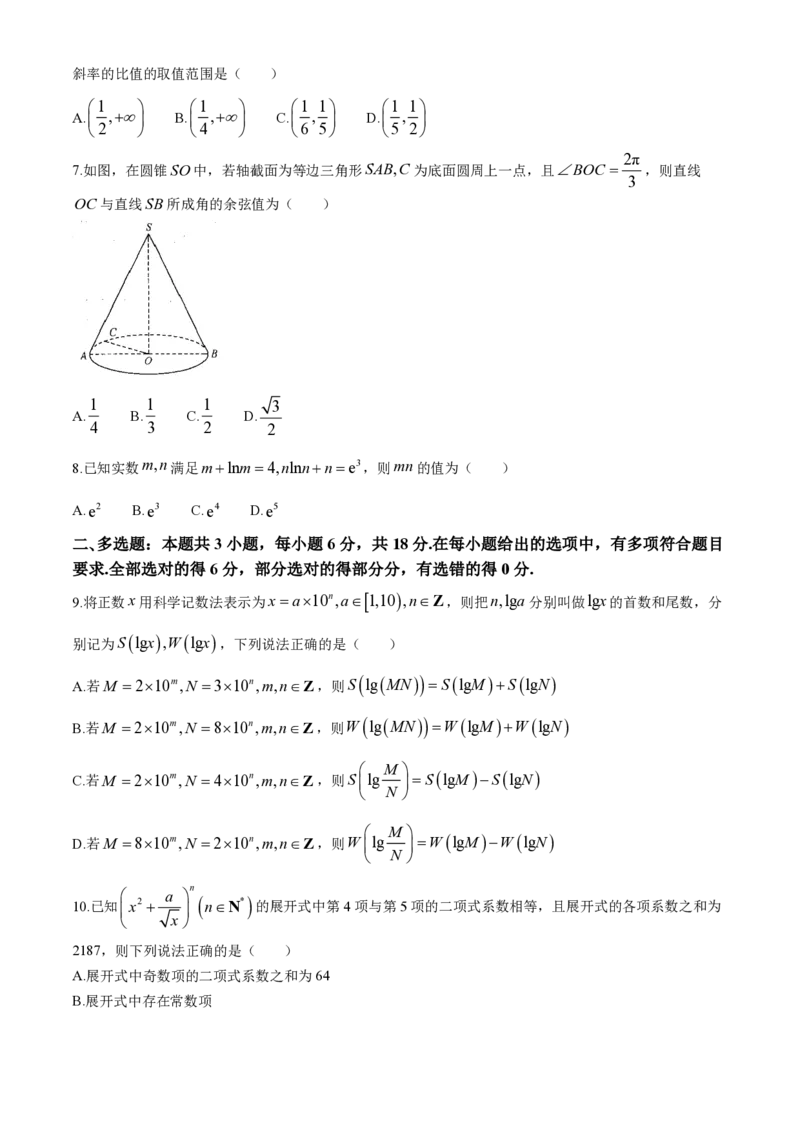19 19 5 5 x2 y2 6.已知椭圆C:  1(ab0)的左顶点､上顶点分别为A,B，右焦点为F ，过F 且与x轴垂直的 a2 b2 15 直线与直线AB交于点E，若直线AB的斜率小于 ,O为坐标原点，则直线AB的斜率与直线OE的 4 学科网（北京）股份有限公司斜率的比值的取值范围是（ ） 1  1  1 1 1 1 A. ,  B. ,  C. ,  D. ,  2  4  6 5 5 2 2π 7.如图，在圆锥SO中，若轴截面为等边三角形SAB,C 为底面圆周上一点，且BOC  ，则直线 3 OC与直线SB所成角的余弦值为（ ） 1 1 1 3 A. B. C. D. 4 3 2 2 8.已知实数m,n满足mlnm4,nlnnne3，则mn的值为（ ） A.e2 B.e3 C.e4 D.e5 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9.将正数x用科学记数法表示为xa10n,a1,10,nZ，则把n,lga分别叫做lgx的首数和尾数，分 别记为Slgx,Wlgx ，下列说法正确的是（ ） A.若M 210m,N 310n,m,nZ，则S  lgMN SlgMSlgN B.若M 210m,N 810n,m,nZ，则W  lgMN WlgMWlgN  M  C.若M 210m,N 410n,m,nZ，则S  lg  SlgMSlgN  N   M  D.若M 810m,N 210n,m,nZ，则W  lg  WlgMWlgN  N  n  a  10.已知  x2    nN* 的展开式中第4项与第5项的二项式系数相等，且展开式的各项系数之和为  x  2187，则下列说法正确的是（ ） A.展开式中奇数项的二项式系数之和为64 B.展开式中存在常数项 学科网（北京）股份有限公司C.展开式中含x4项的系数为560 3 D.展开式中系数最大的项为 672x2 11.在平面直角坐标系xOy中，点F 是拋物线Γ: y ax2(a0)的焦点，F 到Γ的准线l的距离为2，点 A是Γ上的动点，过点A且与Γ相切的直线m与y轴交于点B,C 是准线l上的一点，且AC l，则下列 说法正确的是（ ） A.a  4 B.当点A的横坐标为2时，直线m的斜率为1 C.设D3,0 ，则 AD  AC 的最小值为 10 D. OB , AB , BC 成等差数列 三､填空题：本题共 3小题，每小题 5分，共 15分. r r  r r  r r  12.若向量a,b 不共线，且 xab ∥ a yb ，则xy的值为__________. 13.若正数a,b满足a2bab2，则a的最小值是__________. 14.记x 是不小于x的最小整数，例如1.22,22,1.31，则函数 1 f xxx2x  的零点个数为__________. 8 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 15.（本小题满分13分） 7 已知数列 a  的前n项和为S ，且S  ,2a a 0  nN* . n n 3 4 n1 n （1）求 a  的通项公式； n （2）若数列b a log a ，求数列 b  的前n项和T . n n1 2 n n n 16.（本小题满分15分） 在一个不透明的密闭纸箱中装有10个大小､形状完全相同的小球，其中8个白球，2个黑球.小张每次从纸 箱中随机摸出一个小球观察其颜色，连续摸4次，记随机变量X 为小张摸出白球的个数. （1）若小张每次从纸箱中随机摸出一个小球后放回纸箱，求EX 和DX ； （2）若小张每次从纸箱中随机摸出一个小球后不放回纸箱，求X 的分布列. 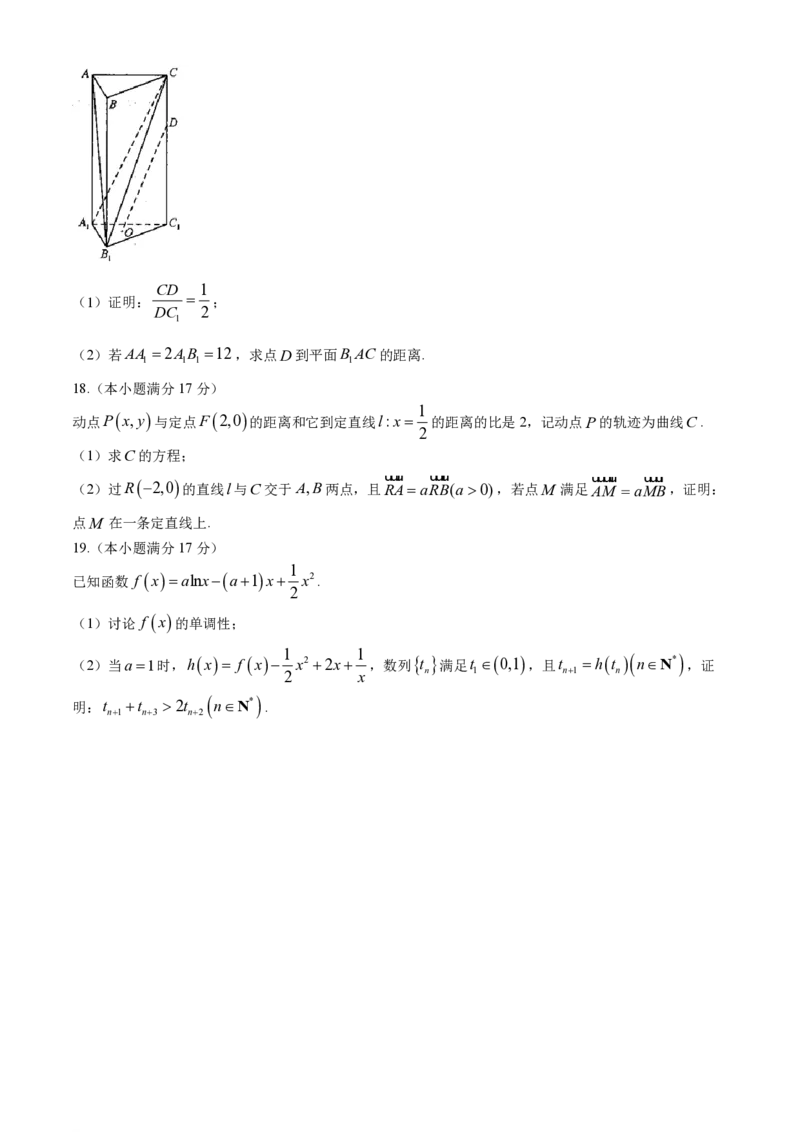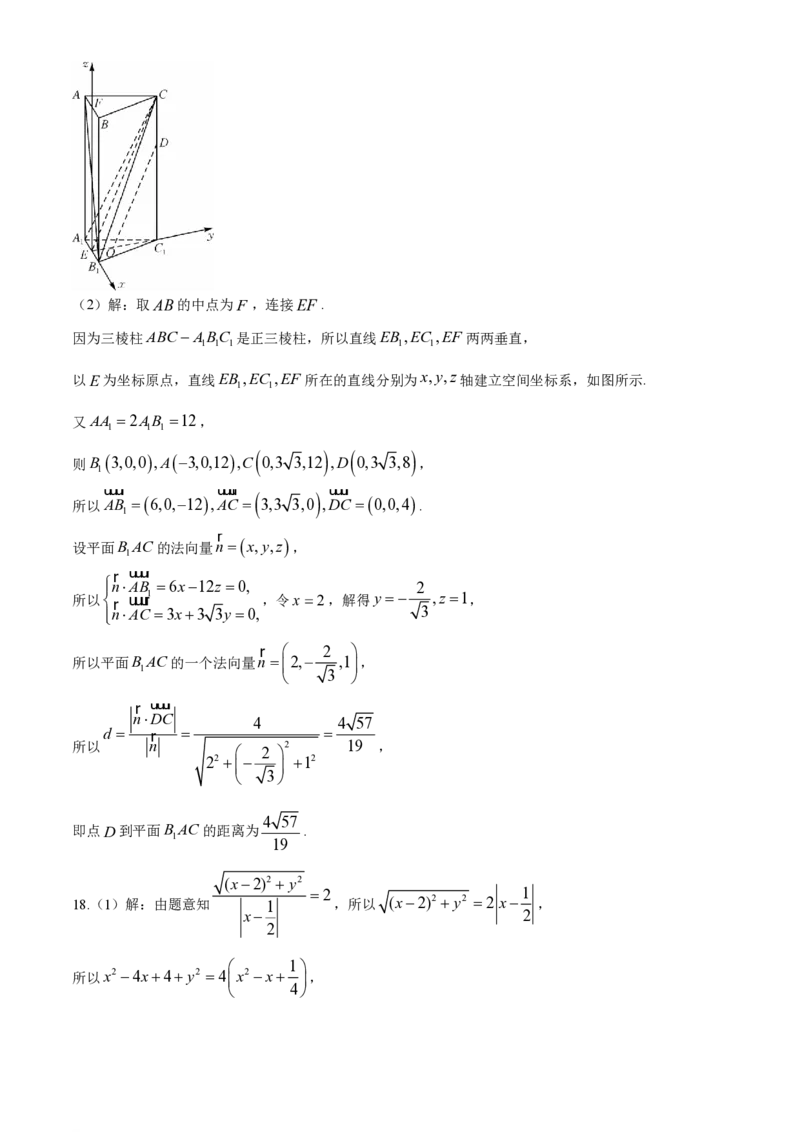17.（本小题满分15分） 如图，在正三棱杜ABCABC 中，O为VABC 的重心，D是棱CC 上的一点，且OD∥平面 1 1 1 1 1 1 1 ABC. 1 1 学科网（北京）股份有限公司CD 1 （1）证明：  ； DC 2 1 （2）若AA 2AB 12，求点D到平面B AC的距离. 1 1 1 1 18.（本小题满分17分） 1 动点Px,y 与定点F2,0 的距离和它到定直线l:x 的距离的比是2，记动点P的轨迹为曲线C. 2 （1）求C的方程； uuur uuur uuuur uuur （2）过R2,0 的直线l与C交于A,B两点，且RAaRB(a 0)，若点M 满足AM aMB，证明： 点M 在一条定直线上. 19.（本小题满分17分） 1 已知函数 f xalnxa1x x2. 2 （1）讨论 f x 的单调性； 1 1 （2）当a1时，hx f x x2 2x ，数列 t  满足t 0,1 ，且t ht  nN* ，证 2 x n 1 n1 n 明：t t 2t  nN* . n1 n3 n2 学科网（北京）股份有限公司2024 届高三年级 TOP 二十名校猜题一·数学 参考答案､提示及评分细则 1.B 因为复数z 25i12i12i，所以z对应的点为 12,1 ，位于第二象限.故选B. 2.C 由已知得，若2a13，解得a1，此时A1,3,B0,1,3 ，符合题意；若2a1a1，解 得a -2，此时A1,3,B8,3,3 ，不符合题意；若2a13a2，解得a 3，此时 A1,7,B2,3,7 ，不符合题意.综上所述：a1.故选C. π 3π 3.C 当2kπ 2kπ （kZ）时，cos0，所以cos„ 0成立，所以 2 2 π 3π “2kπ 2kπ （kZ）”是“cos„ 0”的充分条件；当cos„ 0时， 2 2 π 3π π 3π 2kπ „ „ 2kπ kZ，所以“2kπ 2kπ kZ ”不是“cos„ 0”的必要条件.故 2 2 2 2 选C. π 4.A 将函数y 3sin3x 的图象向右平移 个单位长度得 9   π   π   π  y 3sin  3  x    3sin  3x  ，又y 3sin  3x  的图象关于y轴对称，所以   9   3   3  π π 5π π   kπkZ，解得 kπkZ，当k -1时，取得最小值 .故选A. 3 2 6 6 5.A 记事件A为在某次通电后M､N 有且只有一个需要更换，事件B为M 需要更换，则 PA0.310.210.30.20.38,PAB0.310.20.24，由条件概率公式可得 PAB 0.24 12 PB∣A   .故选A. 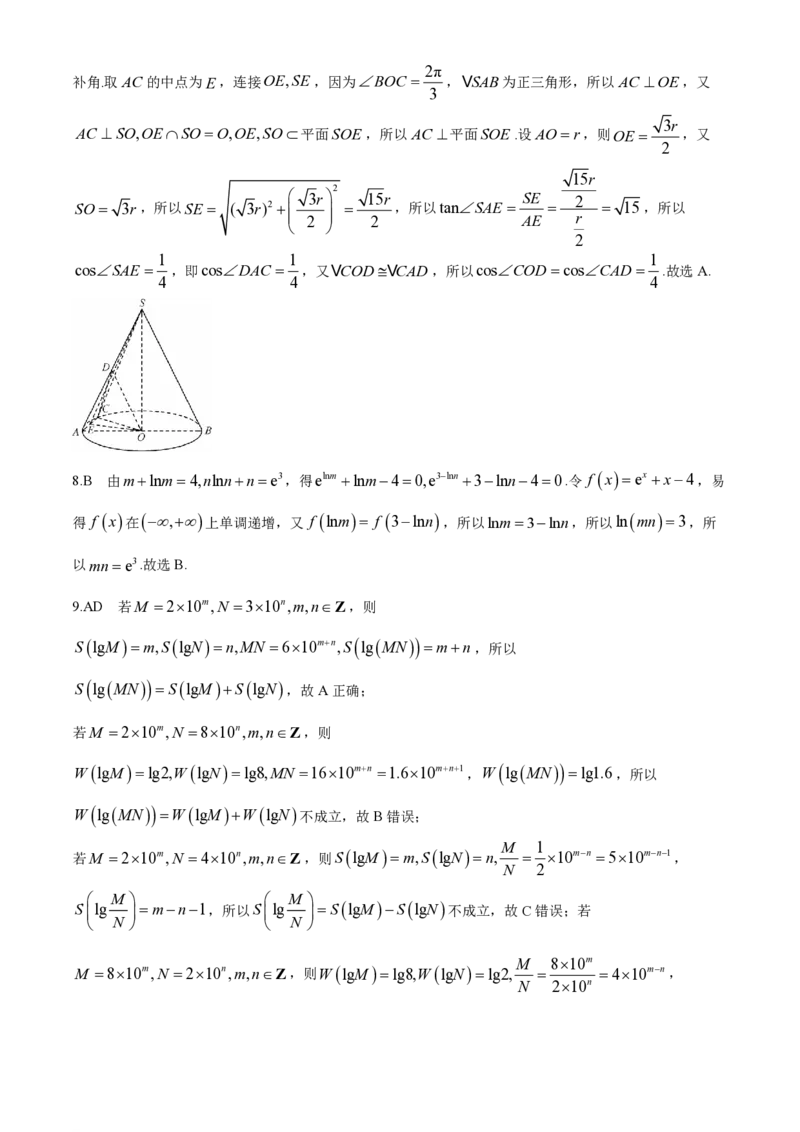PA 0.38 19 b 6.D 由已知得，直线AB的方程为y  xb，设椭圆的焦距为2c(c0)，由题意设点Ec,y  ，则 a 0 bc y  bc b，即E   c, bc b  ，所以 a b bac ，又k  b  15 ，所以 0 a  a  k   AB a 4 OE c ac c b 2 1 1 e  1  ，即 e1.设直线AB的斜率与直线OE的斜率的比值为m，则   a a 4 4 b a c e 1 1 1 1 m   1 ，又 e1，所以 m .故选D bac ac e1 e1 4 5 2 ac 7.A 取SA的中点为D，连接OD,DC，则OD∥SB，所以COD为直线OC与直线SB所成的角或 学科网（北京）股份有限公司2π 补角.取AC的中点为E，连接OE,SE ，因为BOC  ，VSAB为正三角形，所以AC OE，又 3 3r AC SO,OESOO,OE,SO平面SOE ，所以AC 平面SOE .设AOr，则OE  ，又 2 15r 2  3r 15r SE 2 SO 3r，所以SE  ( 3r)2    ，所以tanSAE    15，所以  2  2 AE r   2 1 1 1 cosSAE  ，即cosDAC  ，又VCODVCAD，所以cosCODcosCAD .故选A. 4 4 4 8.B 由mlnm4,nlnnne3，得elnm lnm40,e3lnn 3lnn40.令 f xex x4，易 得 f x 在 , 上单调递增，又 f lnm f 3lnn ，所以lnm3lnn，所以lnmn3，所 以mne3.故选B. 9.AD 若M 210m,N 310n,m,nZ，则 SlgMm,SlgNn,MN 610mn,S  lgMN mn，所以 S  lgMN SlgMSlgN ，故A正确； 若M 210m,N 810n,m,nZ，则 WlgMlg2,WlgNlg8,MN 1610mn 1.610mn1，W  lgMN lg1.6，所以 W  lgMN WlgMWlgN 不成立，故B错误； M 1 若M 210m,N 410n,m,nZ，则SlgMm,SlgNn,  10mn 510mn1， N 2  M   M  S  lg  mn1，所以S  lg  SlgMSlgN 不成立，故C错误；若  N   N  M 810m M 810m,N 210n,m,nZ，则WlgMlg8,WlgNlg2,  410mn， N 210n 学科网（北京）股份有限公司 M   M  W  lg  lg4，所以W  lg  WlgMWlgN ，所以D正确.故选AD.  N   N  10.ACD 由二项式的展开式中第4项与第5项的二项式系数相等，所以C3 C4，解得n 7，又展开式 n n 的各项系数之和为2187，即当x1时，(1a)7 2187，解得a  2.则二项式系数之和为27 128，则 7 1  2  奇数项的二项式系数之和为 12864，故A正确；  x2   的展开式的通项 2  x  T Crx27r   2   r 2rCrx 14 5 2 r ，令14 5 r 0，解得r  28 ，故展开式中不存在常数项，故B错 r1 i  x  r 2 5 5 误；令14 r 4，解得r 4，所以展开式中含x4项的系数为24C4 560，故C正确；由 2 7 2rCr…2r1Cr1 13 16  7 7 解得 „ r„ ，又rN，所以r 5，所以展开式中系数最大的项为 2rCr…2r1Cr1 3 3  7 7 5 3 T 25C5x 14 2 5 672x2 ，故D正确.故选ACD. 51 7 1 11.BC 抛物线Γ: y ax2(a0)化为标准方程为x2  y，因为F 到Γ的准线l的距离为2，所以 a 1 1 1 1 1 2，所以a ，故A错误；由a 得，Γ的方程为y  x2，所以y x，所以直线m的斜 2a 4 4 4 2 1 率k  21，故B正确； AD  AC  AD  AF … FD  12 32  10 ，当且仅当点A是线段 2 DF与Γ的交点时，等号成立，故C正确；  x2  1 x 不妨设点A在第一象限，则点Ax , 0  x 0 ，所以y x，所以直线m的斜率k  0 ，所以直线  0 4  0 2 2 x2 x x2 m的方程为y 0  0 xx ，化简可得，2x x4yx2 0，令x 0，则y  0 ，所以 4 2 0 0 0 4  x2  B0, 0 ，因为AC l，所以Cx ,1 ，所以 4 0   2 2 2  x2  x4 x2  x2   x2  x2 | AB|2 x2  0   x2  0 , OB  0 , BC  x2 1 0   1 0  1 0 ，所以 0 2 0 4 4 0 4 4 4       x4 x2 x2 x4 x2 2 AB   OB  BC  2 x2  0  0 1 0 2 x2  0  0 1，故D错误.故选BC. 0 4 4 4 0 4 2 r r r r  r r  r r  12.1 因为a,b 不共线，所以可设a,b 为一组基向量，因为 xab ∥ a yb ，所以R，使得 学科网（北京）股份有限公司r r r r  r r r r x, xab  a yb ，所以xab ayb ，所以 ，消去，得xy 1. 1y, r  r r r r r r r r r 13.4 因为a2 b a b2，所以a2b a3 b2，因为a,b 为正数，所以 r r r r r r rr r r r rr r r r r r r a2b a3 b2…2 a3b2 2ab a ，即a2b…2ab a ，所以a…4，当且仅当a3 b2，即a 4,b 8 r 时取等号，所以a的最小值是4. 1 1 14.3 令 f x0，则xx2x  ，令gxxx,hx2x  ，则gx 与hx 的交点 8 8 个数即为 f x 的零点个数.当1 x„ 0时，gx0xx0,1 ，又 gx1x1x1xx gx ，所以gx 是周期为1的函数，hx 在R上单调递减， 7 且h11,h0 ,h30，所以可作出gx 与hx 的图象如图， 8 所以gx 与hx 有3个交点，故 f x 的零点个数为3. 7 15.解：（1）因为S  ,2a a 0  nN* ， 3 4 n1 n a 1 1 所以 n1  ，所以数列 a  是公比为 的等比数列， a 2 n 2 n  1 3 a 1    所以 1  2  7 ，解得a 1， S   1 3 1 4 1 2 1 所以a  . n 2n1 1 1 n1 （2）由（1）知b  log  ， n 2n 2 2n1 2n 0 1 2 n2 n1 所以T    L   ， n 2 22 23 2n1 2n 1 0 1 2 n2 n1 所以 T    L   ， 2 n 22 23 24 2n 2n1 学科网（北京）股份有限公司1  1  1   1 1 1 1 n1 22  2n1 n1 1 n1 相减得， T   L       ， 2 n 22 23 2n 2n1 1 2n1 2 2n1 1 2 2n n1 所以T  . n 2n 16.解：（1）由已知得，X B4,0.8 ， 所以EX40.83.2, DX40.810.80.64. CkC4k （2）由已知得，X 服从超几何分布，且PX k 8 2 ,k 2,3,4， C1 10 所以X 的分布列为 X 2 3 4 2 8 1 P 15 15 3 17.（1）证明：连接OC ，延长CO交AB 于E，连接CE，如图所示. 1 1 1 1 EO 1 因为O为VABC 的重心，所以  ， 1 1 1 OC 2 1 因为OD∥平面ABC,OD平面CC E， 1 1 1 平面CC E平面ABC CE， 1 1 1 所以OD∥ EC， CD EO 1 所以   . DC OC 2 1 1 学科网（北京）股份有限公司（2）解：取AB的中点为F ，连接EF . 因为三棱柱ABCABC 是正三棱柱，所以直线EB,EC ,EF 两两垂直， 1 1 1 1 1 以E为坐标原点，直线EB,EC ,EF 所在的直线分别为x,y,z轴建立空间坐标系，如图所示. 1 1 又AA 2AB 12， 1 1 1     则B 3,0,0,A3,0,12,C 0,3 3,12 ,D 0,3 3,8 ， 1 uuur uuur uuur   所以AB 6,0,12,AC  3,3 3,0 ,DC 0,0,4 . 1 r 设平面B AC的法向量n x,y,z ， 1 uuur r  nAB 6x12z 0, 2 所以r uuur1 ，令x  2，解得y  ,z 1， nAC 3x3 3y 0, 3 r  2  所以平面B AC的一个法向量n   2, ,1 ， 1  3  uuur r nDC 4 4 57 d  r   所以 n 2 19 ，  2  22   12    3 4 57 即点D到平面B AC的距离为 . 1 19 (x2)2  y2 2 1 18.（1）解：由题意知 1 ，所以 (x2)2  y2 2 x ， x 2 2  1 所以x2 4x4 y2 4  x2 x ，  4 学科网（北京）股份有限公司y2 化简得，C的方程为x2  1. 3 （2）证明：依题意，设Ax ,y ,Bx ,y ,M x ,y  ， 1 1 2 2 0 0 ①当直线l的斜率为0时，不妨设A1,0,B1,0 ， uuur uuur 因为R2,0 ，所以RA1,0,RB3,0， uuur uuur 1 1 所以RA RB，从而a ， 3 3 uuuur 1 uuur 1 1  1  则AM  MB，即x 1,y  1x ,y ，解得x  ,y 0，即M   ,0 . 3 0 0 3 0 0 0 2 0  2  ②当直线l的斜率不为0时，设l的方程为xty2， xty2,  由 y2 消去x，得  3t2 1  y2 12ty90， x2  1   3 12t 9 则3t2 10且Δ144t2 4  3t2 1  90,y  y  ,y y  ， 1 2 3t2 1 1 2 3t2 1 uuur uuur  RAaRB, y ay , 1 2 因为uuuur uuur ，所以 y  y ay  y , AM aMB,  0 1 2 0 消去a，得y y  y  y y  y  ， 2 0 1 1 2 0 2y y 18 3 所以y  1 2   ， 0 y  y 12t 2t 1 2 3 1 从而x ty 2 2 ， 0 0 2 2  1  1 又  ,0 也在直线x 上.  2  2 1 综上，点M 在直线x 上. 2 a x2 a1xa xax1 19.（1）解：由题意知 fx a1x  . x x x 当a„ 0时，令 fx0，解得x1， 令 fx0，解得0 x1， 所以 f x 在 0,1 上单调递减，在 1, 上单调递增； 学科网（北京）股份有限公司当0a1时，令 fx0，解得0 xa或x1， 令 fx0，解得a x1，所以 f x 在 0,a 上单调递增，在 a,1 上单调递减，在 1, 上单调递 增； 当a1时， fx…0，所以 f x 在 0, 上单调递增； 当a1时，令 fx0，解得0 x1或xa，令 fx0，解得1 xa， 所以 f x 在 0,1 上单调递增，在 1,a 上单调递减，在 a, 上单调递增. 1 x1 （2）证明：当a1时，hxlnx ，则hx ， x x2 令hx0，得0 x1；令hx0，得x1， 所以hx 在 0,1 上单调递减，在 1, 上单调递增，所以hx…h11， 因为t 0,1,t ht 1,t ht 1,L ,t ht 1， 1 2 1 3 2 n1 n 要证t t 2t ，即证t t t t ， n1 n3 n2 n3 n2 n2 n1 又t ht ,t ht  ，即证ht t ht t . n3 n2 n2 n1 n2 n2 n1 n1 2  1 3 1  x  令mxhxx lnxxx…1，则 x2 x1   2   4 ， x mx  0 x2 x2 所以mx 在 1, 上单调递减，且mx„ m10， 因为t t ht t mt  ， n2 n1 n1 n1 n1 又t 1，所以mt 0， n1 n1 所以t t 0，则t t ， n2 n1 n2 n1 所以mt mt  ，即ht t ht t ， n2 n1 n2 n2 n1 n1 所以t t t t 成立，证毕. n3 n2 n2 n1 学科网（北京）股份有限公司