浙江省七彩阳光新高考研究联盟2023-2024学年高三下学期开学考试数学答案(1)_2024年2月_022月合集_2024届浙江省七彩阳光新高考研究联盟高三下学期开学考试

2023 学年第二学期浙江七彩阳光新高考研究联盟返校考 高三数学参考答案 一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是 符合题目要求的。 题号 1 2 3 4 5 6 7 8 答案 B B D A C A D C 8.提示：由题意易得a 0，由 n 高三数学 答案 第1页 共5页 a n a n + 2 = a 2n + 1 + n 得 a a n + n + 2 1 = a n + a n 1 + a n n a n + 1  a n + a n 1  a a 2 1 = 2 ，所以A正确；且 a n = a n a n −1  a a n −1 n − 2  a a 2 1  2 n −1 ，所以 S 10  1 + 2 +  + 2 9 = 2 10 − 1 = 1 0 2 3 ，故C错误； 由上面知 { a n } 也是递增数列，所以 a 2n + 1 + n = a n a n + 2  a 2n + 2 a 2n + 2 ，即 a 2n + 2 − a 2n + 1  a 2n +1 − a 2n + 2 n  a 2n +1 − a 2n ，所以B正确； 由 上得 a a n + n + 2 1 = a n + a n 1 + a n n a n + 1  a n + a n 1 + 2 n n −1  2 n = a n + a n 1 + 2 n 2 n −1 ，累加得 a na + n 1  a a 2 1 + 1 2 + 2 2 3 + 3 2 5 +  + n 2 2 − n 1 − 3 ( n  2 ) , 用错位相减法可求得 1 2 + 2 2 3 + 3 2 5 +  + n 2 −2 n 1− 3 = 8 9 − 9 3 n  2 +2 1n − 3 ( n  2 ) , 所以 a n +1 a n = 2 + 8 9 − 9 3 n  2 + 2 1 n − 3  3 ，故D正确． 二、多项选择题：本题共3小题。每小题6分，共18分．在每小题给出的四个选项中，有多项符合 题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分． 题号 9 10 11 答案 BCD BC ABD 11.提示：由 f(x)g(y)− f(y)g(x)= f(x−y)得 f ( y ) g ( x ) − f ( x ) g ( y ) = f ( y − x ) ， 所以 f(y−x)=−f(x−y)，故 f(x)是奇函数，所以A正确； 由 g ( x ) g ( y ) − f ( x ) f ( y ) = g ( x − y ) 得 g ( y ) g ( x ) − f ( y ) f ( x ) = g ( y − x ) ， 所以 g ( y − x ) = g ( x − y ) ，故 g ( x ) 是偶函数，所以B正确； 由题意得 f(x−y)−g(x−y)= f(x)g(y)− f(y)g(x)−g(x)g(y)+ f(x)f(y) =[f(y)+g(y)][f(x)−g(x)]，令y=1得 f(x−1)−g(x−1)=[f(1)+g(1)][f(x)−g(x)] 由 f ( x ) 是奇函数得 f ( 0 ) = 0 ，且[g(0)]2−[f(0)]2 =g(0)， g ( 0 )  0 ，解得 g ( 0 ) = 1 当 f(1)+g(1)=1时， f(100)−g(100)=[f(0)−g(0)]=−1，所以C错误． 由题意得 f(x−y)+g(x−y)= f(x)g(y)− f(y)g(x)+g(x)g(y)− f(x)f(y) =[g(y)− f(y)][f(x)+g(x)]，令y=1得 f(x−1)+g(x−1)=[g(1)− f(1)][f(x)+g(x)] 当 f(1)−g(1)=1时， f(100)+g(100)=(−1)100[f(0)+g(0)]=1，所以D正确． {#{QQABSYCAggCAAAIAAAhCQwlqCkOQkACACIoOAAAEsAAByANABAA=}#}三、填空题：本题共3小题，每小题5分，共15分． 12．32； 13． 高三数学 答案 第2页 共5页 [ − 3 2 ,3 ] ； 14． 6 6 ； 14．提示：设O是正四面体 A B C D 内切球的球心，由体积法可求正四面体 A B C D 6 的内切球半径为 ， 12 正四面体 A B C D 6 的外接球半径为 ，则 4 P A 2 + P B 2 + P C 2 + P D 2 = P A 2 + P B 2 + P C 2 + P D 2 =(PO+OA)2+(PO+OB)2+(PO+OC)2+(PO+OD)2 2 2 =4PO +2PO(OA+OB+OC+OD)+4OA = 4 P O 2 + 0 + 4 ( 6 4 ) 2 = 4 P O 2 + 3 2 = 5 3 ，即 P O = 1 6 2 ， 所以 P 是正四面体ABCD内切球上一点，故 P A 的最小值为 O A − P A = 6 4 − 1 6 2 = 6 6 ． 四、解答题：本题共5小题，共77分解答应写出文字说明、证明过程或演算步骤。 15．【解析】（1）设 { a n } 的公差为d ，由题意得， 2 a 1 + 1 2 d = 5 ( a 1 + 2 d ) ，所以，d =3.....3分 故， { a n } 的通项公式为 a n = a 1 + ( n − 1 ) d = 3 n − 1 ． ……5分 （2）由 a n b n = a n + 2 b n + 1 得， b n + b n 1 = a a n n + 2 = 3 3 n n − + 1 5 ， b b b b a a a 10 所以 n = n  n−1 2 = n−1 n−2 1 = ， b b b b a a a (3n+2)(3n−1) 1 n−1 n−2 1 n+1 n 3 所以 b n = ( 3 n + 1 2 0 ) ( 3 n − 1 ) ． ……8分 10 10 1 1 由b = = ( − )得 .......................10分 n (3n+2)(3n−1) 3 3n−1 3n+2 S n = 1 0 3 ( 1 2 − 1 5 + 1 5 − 1 8 +  + 3 n 1 − 1 − 3 n 1 + 2 ) = 1 0 3 ( 1 2 − − 3 n 1 + 2 ) = 3 5 n n + 2 ． ……13分 16．【解折】（1）在梯形ABCD中，由AD∥BC，BC⊥CD，BC=2CD=2AD，得AB⊥ AC． 又平面ABCD⊥平面PAC，平面ABCD 平面PAC= AC，AB平面ABCD， 所以AB ⊥平面PAC，所以平面PAB⊥平面PAC ……3分 又等边PAC，M 是棱PA的中点，所以MC⊥PA， {#{QQABSYCAggCAAAIAAAhCQwlqCkOQkACACIoOAAAEsAAByANABAA=}#}所以 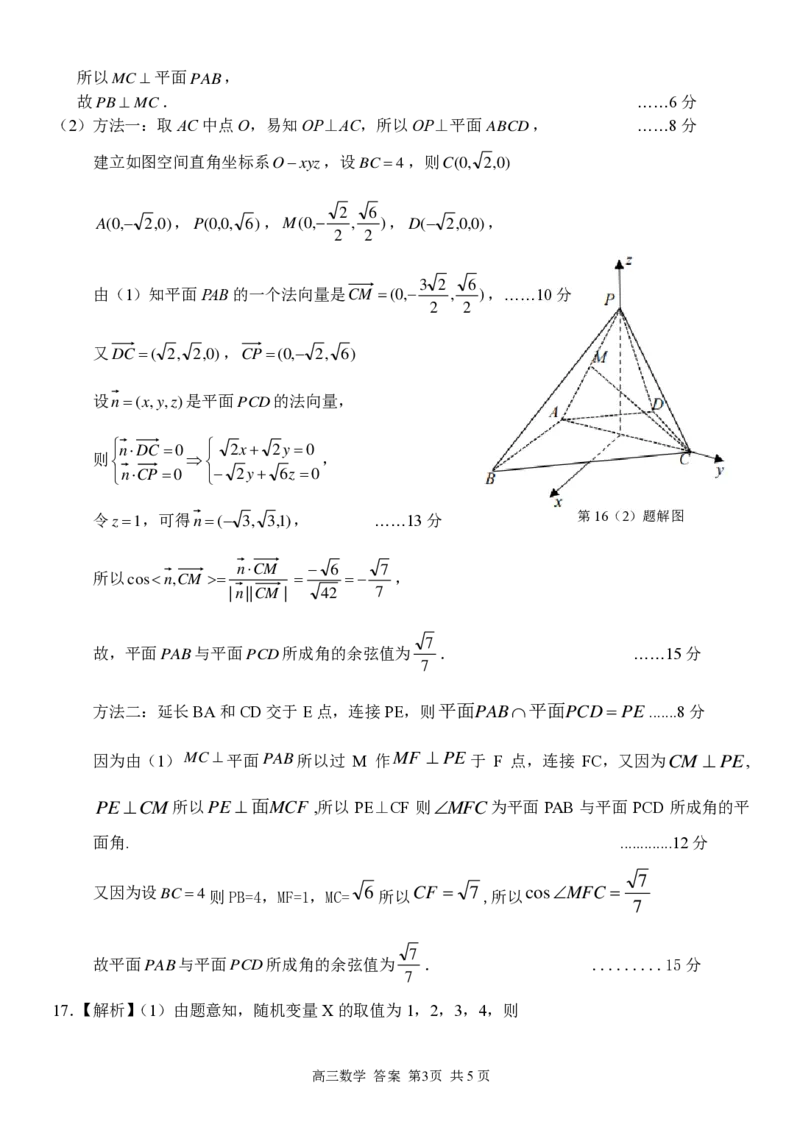第16（2）题解图 高三数学 答案 第3页 共5页 M C ⊥ 平面 P A B ， 故PB⊥MC． ……6分 （2）方法一：取AC中点O，易知OP⊥AC，所以OP⊥平面 A B C D ， ……8分 建立如图空间直角坐标系O−xyz，设BC=4，则C(0, 2,0) A(0,− 2,0)，P(0,0, 6)， M ( 0 ,− 2 2 , 6 2 ) ，D(− 2,0,0)， 由（1）知平面PAB的一个法向量是 C M = ( 0 ,− 3 2 2 , 6 2 ) ，……10分 又DC=( 2, 2,0)， C P = ( 0 ,− 2 , 6 ) 设n=(x,y,z)是平面 P C D 的法向量， nDC=0  2x+ 2y=0 则  ，  nCP=0  − 2y+ 6z=0 令 z = 1 ，可得 n = ( − 3 , 3 ,1 ) ， ……13分 所以 c o s  n , C M  = | n n  C || C M M | = − 4 6 2 = − 7 7 ， 故，平面 P A B 与平面 P C D 所成角的余弦值为 7 7 ． ……15分 方法二：延长BA和CD交于E点，连接PE，则 平 面 P A B  平 面 P C D = P E .......8分 因为由（1） M C ⊥ 平面 P A B 所以过 M 作 M F ⊥ P E 于 F 点，连接 FC，又因为CM ⊥PE, PE⊥CM所以PE⊥面MCF ,所以 PE⊥CF 则  M F C 为平面 PAB 与平面 PCD 所成角的平 面角. .............12分 又因为设BC=4则PB=4，MF=1，MC= 6 所以 C F = 7 7 cosMFC = ,所以 7 7 故平面PAB与平面PCD所成角的余弦值为 ． .........15分 7 17．【解析】（1）由题意知，随机变量X的取值为1，2，3，4，则 {#{QQABSYCAggCAAAIAAAhCQwlqCkOQkACACIoOAAAEsAAByANABAA=}#}1 P(X =1)= ， 3 高三数学 答案 第4页 共5页 P ( X = 2 ) = 2 3  1 3 = 2 9 2 1 4 ，P(X =3)=( )2 = ， 3 3 27 P ( X = 4 ) = ( 2 3 ) 3 = 8 2 7 ，......4分 即X的分布列为 所以 E ( X ) = 1  1 3 + 2  2 9 + 3  4 2 7 + 4  8 2 7 = 6 2 5 7 ． ……7分 （2）易知小朋友套娃娃未成功的概率为 ( 2 3 ) 4 = 1 8 6 1 ， 16 65 则小朋友套娃娃成功的概率为1− = ． ……10分 81 81 记摊主每天利润为 Y 元，则 Y 的期望为 E ( Y ) = 3 0  [ E ( X )  1 0 − 6 8 5 1  1 8 ] = 3 0  [ 6 2 5 7  1 0 − 6 8 5 1  1 8 ] = 2 6 0 9 0 ， ……15分 故摊主每天利润的期望为 2 6 0 9 0 元． 18．【解析】（1）设 A ( x 1 , y 1 ) ， B ( x 2 , y 2 ) ，直线 A B 方程 为 x = m y + 1 ，与椭圆方程联立，得 ( m 2 + 2 ) y 2 + 2 m y − 1 = 0 ， y 1 + y 2 = m − 22 m + 2 ， y 1 y 2 = m −2 1 + 2 ， ……2分 x 1 + x 2 = m ( y 1 + y 2 ) + 2 = m 42 + 2 ， x 1 x 2 = ( m y 1 + 1 ) ( m y 2 + 1 ) = − 2 m m 2 2 + + 2 2 ， 所以 k 1  k 2 = x 1 y − 1 2 x 2 y − 2 2 = x 1 x 2 − y 2 1 ( y x 2 1 + x 2 ) + 2 = − 3 + 2 2 2 ． ……6分 （2）设 A ( x 1 , y 1 ) ， B ( x 2 , y 2 ) ， C ( x 3 , y 3 ) ， D ( x 4 , y 4 ) ，直线AC，BD方程分别为 x=ny+ 2 ， 1 x = n 2 y + 2 ，nn =−1， 1 2 x −2 2n −2 2n 联立x=ny+ 2 与 +y2 =1得y = 1 ，同理y = 2 , 1 2 1 n2+2 2 n2+2 1 2 联立 x = n 1 y + 2 X 1 2 3 4 x −2 2n −2 2n 与 −y2 =1得y = 1 ，同理y = 2 , ……10分 2 3 n2−2 4 n2−2 1 2 1 1 所以四边形ABCD面积为S = |AC||BD|= 1+n2 |y −y | 1+n2 |y −y | 2 2 1 1 3 2 2 4 P 1 3 2 9 4 27 8 2 7 {#{QQABSYCAggCAAAIAAAhCQwlqCkOQkACACIoOAAAEsAAByANABAA=}#}高三数学 答案 第5页 共5页 = 1 2 n 21 + n 22 + 2  8 | n 241 | − n 4 1 | |  8 | n 242 | − n 4 2 | | = | 6 4 4 ( n 21 n + 21 + 2 n 2 n ) 222 + − 2 2 5 | ……13分 令t=n2+n2，易知 1 2 0  n 21  2 ， 0  n 22  2 ，且 n n1 2 = − 1 5 ，则t[2, )， 2 S = 6 4 2 5 ( − t + 4 t 2 2 ) ， 因为 S 642 128 关于t单调递增，所以S = = ， min 25−16 9 当S 取最小值 1 2 9 8 时，t=2， n 1 = 1 , n 2 = − 1 ，经检验满足题意． ……17分 19．【解析】（1）当 a = 1 时， f ( x ) = e x − 2 x + ln x ， f ' ( x ) = e x − 2 + 1 x ...........2分 f (1 ) = e − 2 ， f'(1)=e−1 所以所求切线方程为 y = ( e − 1 ) ( x − 1 ) + ( e − 2 ) ，即y=(e−1)x−1． ……5分 （2）由 f ( x )  0 得，ex −axax−aln(ax) （*） x−a 令g(x)=x−alnx，g'(x)= ，易知 x g ( x ) 在 ( 0 , a ) 上单调递减， ( a ,+  ) 上单调递增 当a(0,e]时，因为 x  [1 ,+  ) ，所以 e x  e  a ， a x  a ， ex 所以不等式（*）等价于g(ex)g(ax)，也等价于ex ax，即a ， x ex ex(x−1) 又( )'= 0，所以 x x2 x e x 在x[1,+)上单调递增， x e x  e ， 故a(0,e]满足题意． ……11分 当 a  ( e ,+  ) ex 时，由 在 x [1 ,+  ) 上单调递增知， e x = a x 在 [1 ,+  ) 上有唯一实数解，设为 x 0 ， 且x (1,+)，ex 0 =ax ，ln(ax )=x ． 0 0 0 0 所以 f ( x 0 ) = e x0 − 2 a x 0 + a ln a x 0 = 0 ， 所以要使 f(x)0在x[1,+)上恒成立，则 f'(x )=0， 0 a a a(x −1)2 另一方面， f'(x )=ex 0 −2a+ =ax −2a+ = 0 0，矛盾。 0 x 0 x x 0 0 0 故a(e,+)不满足题意， 综合得，a的取值范围为0ae． ……17分 （2）解法二：先证明 f(1)0对任意a0恒成立， {#{QQABSYCAggCAAAIAAAhCQwlqCkOQkACACIoOAAAEsAAByANABAA=}#}设g(a)= f(1)=e−2a+alna（ 高三数学 答案 第6页 共5页 a  0 ），g'(a)=lna−1，当a(0,e)时，g'(a)0，g(a)在(0,e) 上单调递减， a  ( e ,+  ) 时， g '( a )  0 ， g ( a ) 在 ( e ,+  ) 上单调递增， 所以 g ( a )  g ( e ) = 0 ，即 f (1 )  0 对任意a0恒成立． 又 f '( x ) = e x − 2 a + a x ，设 h ( x ) = e x − 2 a + a x ，则 h '( x ) = e x − a x 2 ， 易知h'(x)单调递增，所以h'(x)h'(1)． h'(1)=e−a0 h'(x)0 当a(0,e]时， ， ， 所以 h ( x ) 单调递增， f '( x ) = h ( x )  h (1 ) = e − a  0 ， f ( x ) 单调递增， 所以 f ( x )  f (1 )  0 ，符合题意． ……11分 当a(e,+)时，同解法一． ……17分 {#{QQABSYCAggCAAAIAAAhCQwlqCkOQkACACIoOAAAEsAAByANABAA=}#}