文档内容
台州市 2024 届高三第二次教学质量评估试题
数 学
本试卷共4页,19小题,满分150分,考试用时120分钟。
一、单项选择题:本题共 8小题,每小题5分,共40分。在每小题给出的四个选项中,只有
一项是符合题目要求的。
1.已知集合 , ,则 ( )
A. B. C. D.
2.在复平面内,复数 ( 为虚数单位),则( )
A. 的实部为2 B.
C. D. 对应的点位于第一象限
3.已知平面向量 , ,若 ,则实数 ( )
A.-1 B.-2 C.1 D.2
4.已知正项等比数列 满足 ,且 , , 成等差数列,则数列 的前 项和为( )
A. B. C. D.
5.已知x,y为正实数,则可成为“ ”的充要条件的是( )
A. B.
C. D.
6.在 中,角A,B,C所对的边分别为a,b,c.若 ,则 的最大值为( )
A. B. C. D.3
7.房屋建造时经常需要把长方体砖头进行不同角度的切割,以契合实际需要.已知长方体的规格为
24cm×11cm×5cm,现从长方体的某一棱的中点处作垂直于该棱的截面,截取 1 次后共可以得到
学科网(北京)股份有限公司12cm×11cm×5cm, , 三种不同规格的长方体.按照上述方式对第
1次所截得的长方体进行第 2次截取,再对第2次所截得的长方体进行第 3次截取,则共可得到体积为
165cm³的不同规格长方体的个数为( )
A.8 B.10 C.12 D.16
8.设 , 是双曲线 : 的左、右焦点,点M,N分别在双曲线 的左、右两
支上,且满足 , ,则双曲线 的离心率为( )
A.2 B. C. D.
二、多项选择题:本题共 3小题,每小题6分,共18分。在每小题给出的选项中,有多项符
合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.某同学最近6次考试的数学成绩为107,114,136,128,122,143.则( )
A.成绩的第60百分位数为122 B.成绩的极差为36
C.成绩的平均数为125 D.若增加一个成绩125,则成绩的方差变小
10.已知正方体 的棱长为1, 为平面 内一动点,且直线 与平面 所
成角为 ,E为正方形 的中心,则下列结论正确的是( )
A.点 的轨迹为抛物线
B.正方体 的内切球被平面 所截得的截面面积为
C.直线 与平面 所成角的正弦值的最大值为
D.点 为直线 上一动点,则 的最小值为
学科网(北京)股份有限公司11. 已 知 是 定 义 域 为 的 非 常 数 函 数 , 若 对 定 义 域 内 的 任 意 实 数 x , y 均 有
,则下列结论正确的是( )
A. B. 的值域为
C. D. 是奇函数
三、填空题:本题共3小题,每小题5分,共15分。
12. 的展开式中 的系数为___________(用数字作答).
13.某班有A,B两个学习小组,其中A组有2位男生,1位女生,B组有2位男生,2位女生.为了促进小组
之间的交流,需要从 A,B 两组中随机各选一位同学交换,则交换后 A 组中男生人数的数学期望为
___________.
14.已知关于x的不等式 恒成立,则实数a的取值范围是___________.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
已知数列 满足 , .
(1)求 (只需写出数值,不需要证明);
(2)若数列 的通项可以表示成 的形式,求 ,
.
16.(15分)
台州是全国三大电动车生产基地之一,拥有完整的产业链和突出的设计优势.某电动车公司为了抢占更多的
市场份额,计划加大广告投入、该公司近5年的年广告费 (单位:百万元)和年销售量 (单位:百万
辆)关系如图所示:令 ,数据经过初步处理得:
学科网(北京)股份有限公司44 4.8 10 40.3 1.612 19.5 8.06
现有① 和② 两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,
b,m,n均为常数.
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)根据(1)的分析选取拟合程度更好的回归分析模型及表中数据,求出y关于x的回归方程,并预测
年广告费为6(百万元)时,产品的年销售量是多少?
(3)该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时
也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响
外还受随机变量 影响,设随机变量 服从正态分布 ,且满足 .在(2)的
条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-
年研发经费-随机变量).
附:①相关系数 ,
回归直线 中公式分别为 , ;
②参考数据: , , , .
17.(15分)
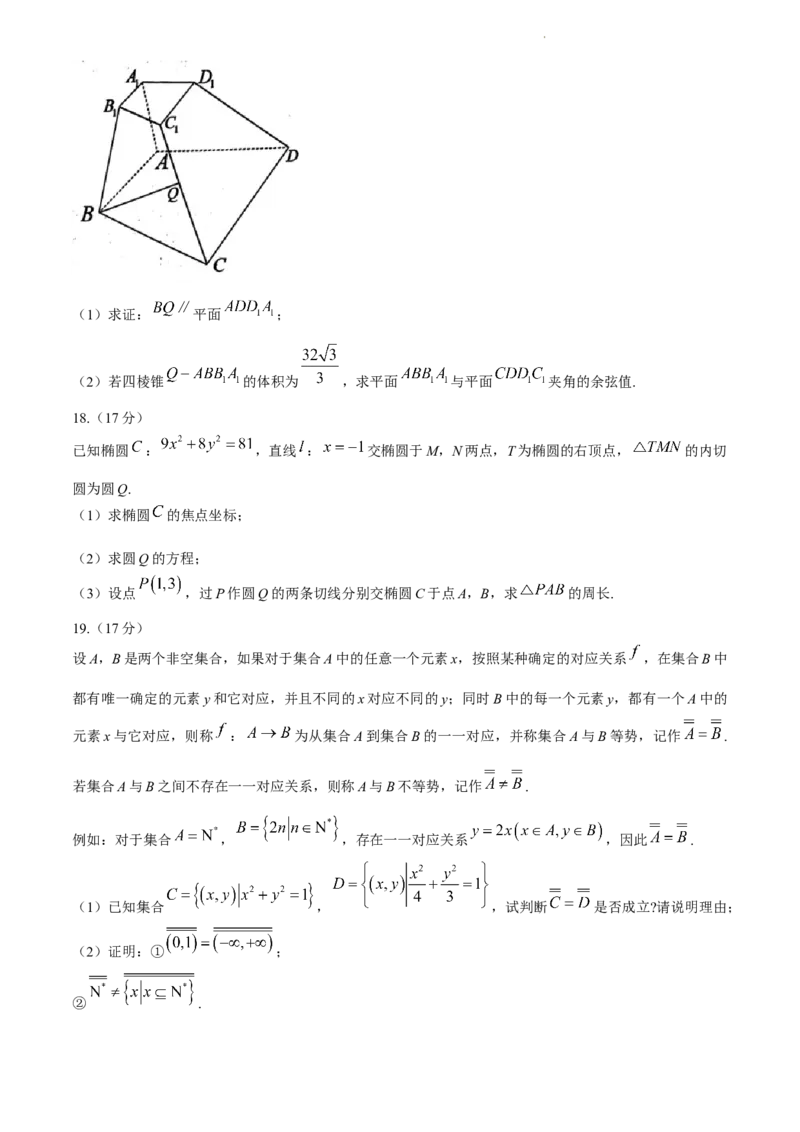
如图,已知四棱台 中, , , , , ,
,且 , 为线段 中点,
学科网(北京)股份有限公司(1)求证: 平面 ;
(2)若四棱锥 的体积为 ,求平面 与平面 夹角的余弦值.
18.(17分)
已知椭圆 : ,直线 : 交椭圆于M,N两点,T为椭圆的右顶点, 的内切
圆为圆Q.
(1)求椭圆 的焦点坐标;
(2)求圆Q的方程;
(3)设点 ,过P作圆Q的两条切线分别交椭圆C于点A,B,求 的周长.
19.(17分)
设A,B是两个非空集合,如果对于集合A中的任意一个元素x,按照某种确定的对应关系 ,在集合B中
都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的
元素x与它对应,则称 : 为从集合A到集合B的一一对应,并称集合A与B等势,记作 .
若集合A与B之间不存在一一对应关系,则称A与B不等势,记作 .
例如:对于集合 , ,存在一一对应关系 ,因此 .
(1)已知集合 , ,试判断 是否成立?请说明理由;
(2)证明:① ;
② .
学科网(北京)股份有限公司学科网(北京)股份有限公司参考答案
一、单项选择题:本题共 8小题,每小题5分,共40分。在每小题给出的四个选项中,只有
一项是符合题目要求的。
题号 1 2 3 4 5 6 7 8
答案 D B D A D C B B
二、多项选择题:本题共 3小题,每小题6分,共18分。在每小题给出的选项中,有多项符
合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
题号 9 10 11
答案 BCD BCD AC
三、填空题:本题共3小题,每小题5分,共15分。
12.20 13. 14.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(本小题满分13分)
解(1) , , , ,
故数列 的周期为3, .
(2)由 , ,得到
解得 , .
备注:以下解法不扣分
因为 的周期为3,所以
又由 ,得到
解得 .
学科网(北京)股份有限公司16.(本小题满分15分)
解:(1)设模型①和②的相关系数分别为 , .
由题意可得:
.
所以 ,由相关系数的相关性质可得,模型②的拟合程度更好.
(2)
又由 , ,得 ,
所以 ,即回归方程为 .
当 时, ,
因此当年广告费为6(百万元)时,产品的销售量大概是13(百万辆).
(3)净利润为 , ,
令 ,
所以 .
可得 在 上为增函数,在 上为减函数.
所以 ,
由题意有: ,即 ,
,
学科网(北京)股份有限公司即该公司年净利润大于1000(百万元)的概率为0.3.
17.(本小题满分15分)
解:(1)分别延长线段 , , , 交于点 ,将四棱台补成四棱锥 .
∵ ,∴ ,∴ ,
取 的中点 ,连接 , ,
∵ ,∴四边形 为平行四边形.
∴ ,又 平面 , 平面 ,
∴ 平面 ;
(不补成棱锥,直接取 的中点,利用梯形中位线也不扣分)
(2)由于 ,所以 ,
又梯形 面积为 ,
设 到平面 距离为 ,则 ,得 .
而 , 平面 , 平面 ,
所以 平面 ,
所以点C到平面 的距离与点D到平而的距离相等,
而 ,所以 平面 .
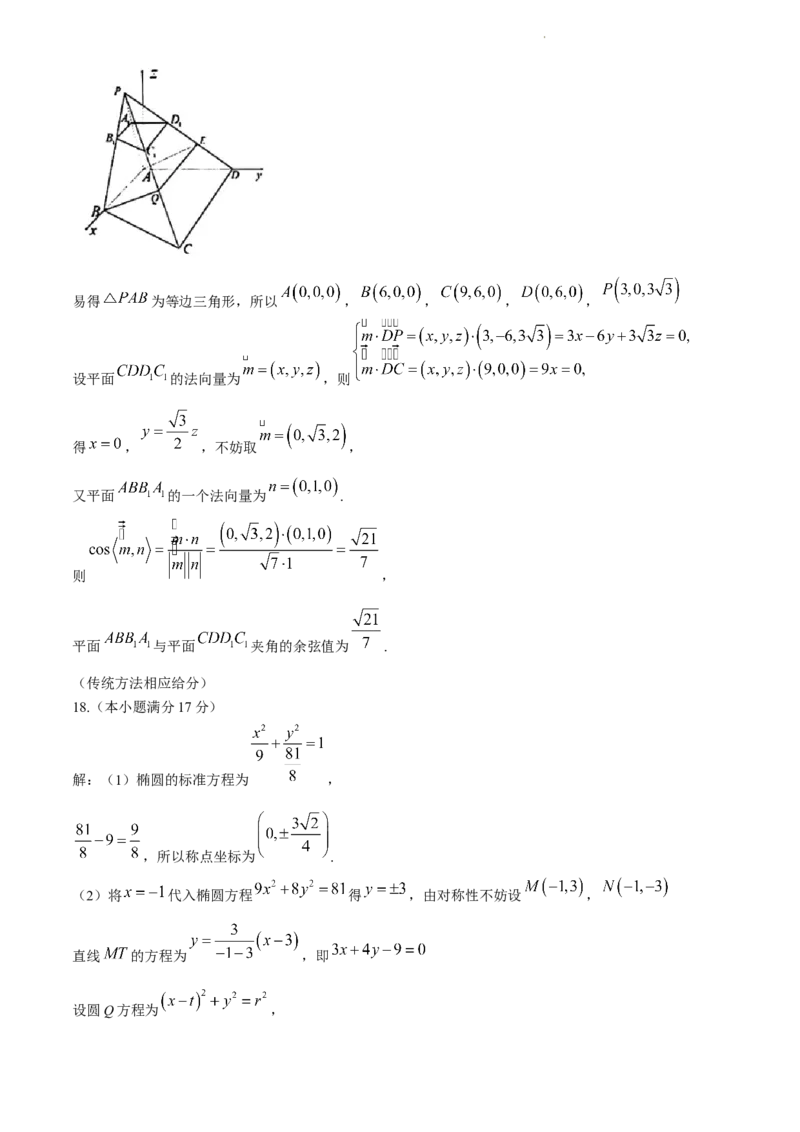
以A为坐标原点,以直线 为x轴,以直线 为y轴,建立空间直角坐标系,如图所示.
学科网(北京)股份有限公司易得 为等边三角形,所以 , , , ,
设平面 的法向量为 ,则
得 , ,不妨取 ,
又平面 的一个法向量为 .
则 ,
平面 与平面 夹角的余弦值为 .
(传统方法相应给分)
18.(本小题满分17分)
解:(1)椭圆的标准方程为 ,
,所以称点坐标为 .
(2)将 代入椭圆方程 得 ,由对称性不妨设 ,
直线 的方程为 ,即
设圆Q方程为 ,
学科网(北京)股份有限公司由于内切圆Q在 的内部,所以 ,
则Q到直线 和直线 的距离相等,即: ,
解得 , ,
所以圆 方程为 .
(用周长与面积求半径的方法相应给分)
(3)显然直线 和直线 的斜率均存在,
设过P作圆Q的切线方程为 ,其中k有两个不同的取值 和 分别为直线 和 的斜
率.
由圆Q与直线相切得: ,化简得: ,
则
由 得 ,
可得 ,
所以
.
同理 ,
所以直线 的方程为
学科网(北京)股份有限公司所以 与圆Q相切,
将 代入 得 ,
所以 ,
又点P到直线 的距离为 ,
设 的周长为 ,则 的面积 ,
解得 .
所以 的周长为 .
19.(本小题满分17分)
解:(1)设 , ,令
则C与D存在一一对应,所以集合 .
(2)①取函数 ,其中 , ,两个集合之间存在一一对应,故
.
备注:函数举例不唯一,只要保证定义域为 ,值域为 即可,
如: 或 等等均给满分,
【若直接利用等势的自反性,未交待反函数关系,而给出定义域为 R,值域为(0,1)的函数.如
, , 扣1分,交传了反函数关系不加分】
②设 , ,
假设 ,即存在对应关系 : 为一一对应,
学科网(北京)股份有限公司对于集合B中的元素 , , ,至少存在一个 ( ,且 )与这三个集合中的某一
个对应,所以集合A中必存在 .
记 ,则 ,故 ,
从而存在 ,使得 ;
若 ,则 ,矛盾;
若 ,则 ,矛盾.
因此,不存在A到B的一一对应,所以 .
学科网(北京)股份有限公司