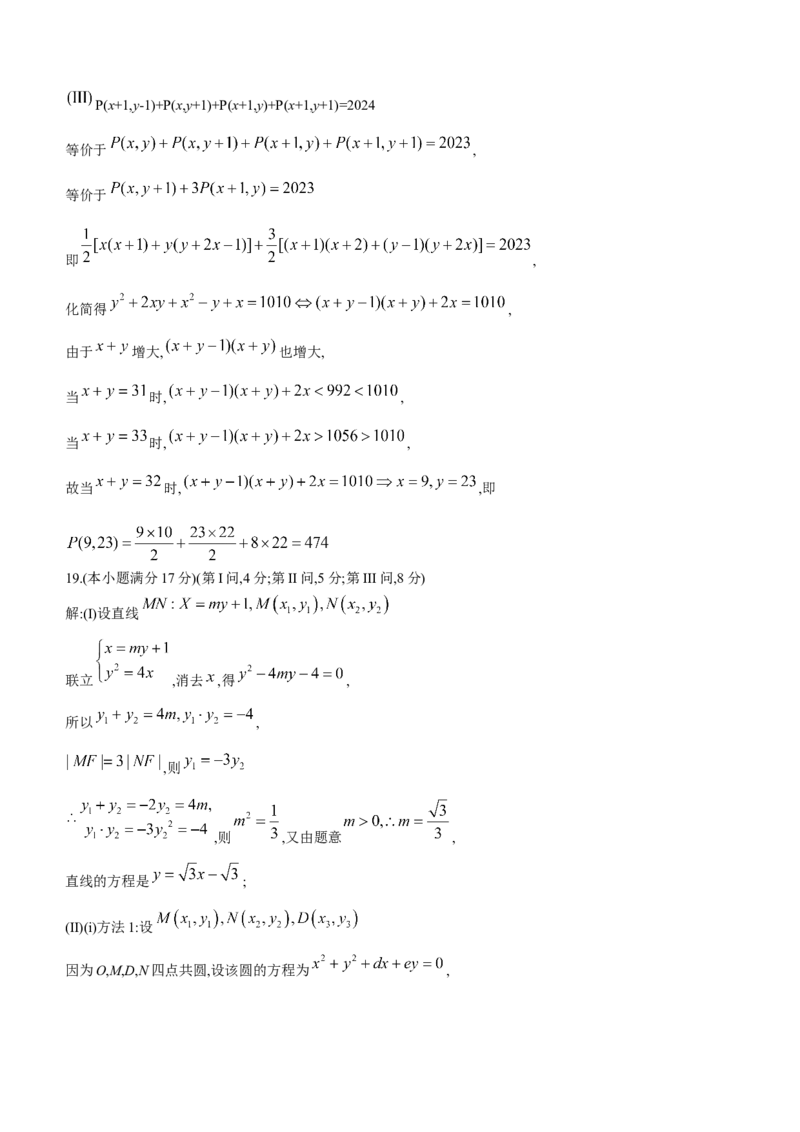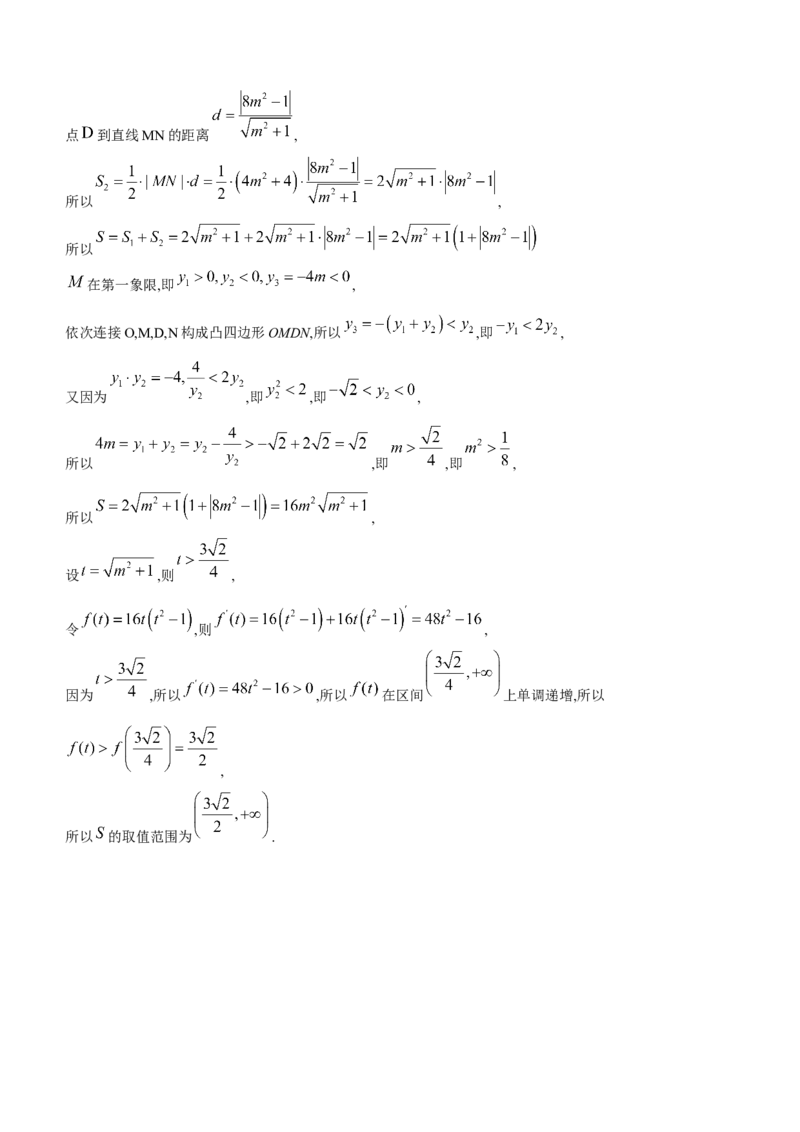文档内容
浙江省五校联盟 2023-2024 学年高三下学期 3 月联考
数学试卷
命题:浙江省杭州第二中学
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要
求.
1.若全集 ,集合A,B及其关系如图所示,则图中阴影部分表示的集合是( )
A. B. C. D.
2.已知 ,且 ,则 与 的夹角的余弦值为( )
A. B. C. D.
3.设b,c表示两条直线, 表示两个平面,则下列说法中正确的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
4.已知角 的终边过点 ,则 ( )
A. B. C. D.
5.设等比数列 的公比为 ,前 项和为 ,则“ ”是“ 为等比数列”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
6.已知实数x,y满足 ,且 ,则 的最小值为( )
A. B.8 C. D.
7.已知双曲线 的左、右焦点分别为 ,点 为双曲线的左顶点,以 为直径的圆交双曲线的一条渐近线于P,Q两点,且 ,则该双曲线的离心率为( )
A. B. C. D.
8.在等边三角形ABC的三边上各取一点D,E,F,满足 ,则三角形ABC的面积的
最大值是( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
部选对的得6分,部分选对的得部分分,有选错的得0分.
9.在学校组织的《青春如火,初心如炬》主题演讲比赛中,有8位评委对每位选手进行评分(评分互不相同),将选
手的得分去掉一个最低评分和一个最高评分,则下列说法中正确的是( )
A.剩下评分的平均值变大 B.剩下评分的极差变小
C.剩下评分的方差变小 D.剩下评分的中位数变大
10.在三棱锥 中,已知 ,点M,N分别是AD,BC的中点,则(
)
A.MN⊥AD B.异面直线AN,CM所成的角的余弦值是
C.三棱锥 的体积为 D.三棱锥 的外接球的表面积为
11.已知函数 ,则( )
A. 的零点为
B. 的单调递增区间为
C.当 时,若 恒成立,则
D.当 时,过点 作 的图象的所有切线,则所有切点的横坐标之和为
三、填空题:本题共3小题,每小题5分,共15分.12.直线 的一个方向向量是 .
13.甲、乙两人争夺一场羽毛球比赛的冠军,比赛为“三局两胜”制.如果每局比赛中甲获胜的概率为 ,乙获胜
的概率为 ,则在甲获得冠军的情况下,比赛进行了三局的概率为 .
14.已知函数 及其导函数 的定义域均为 ,记 ,若 均为偶函数,且当
时, ,则 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
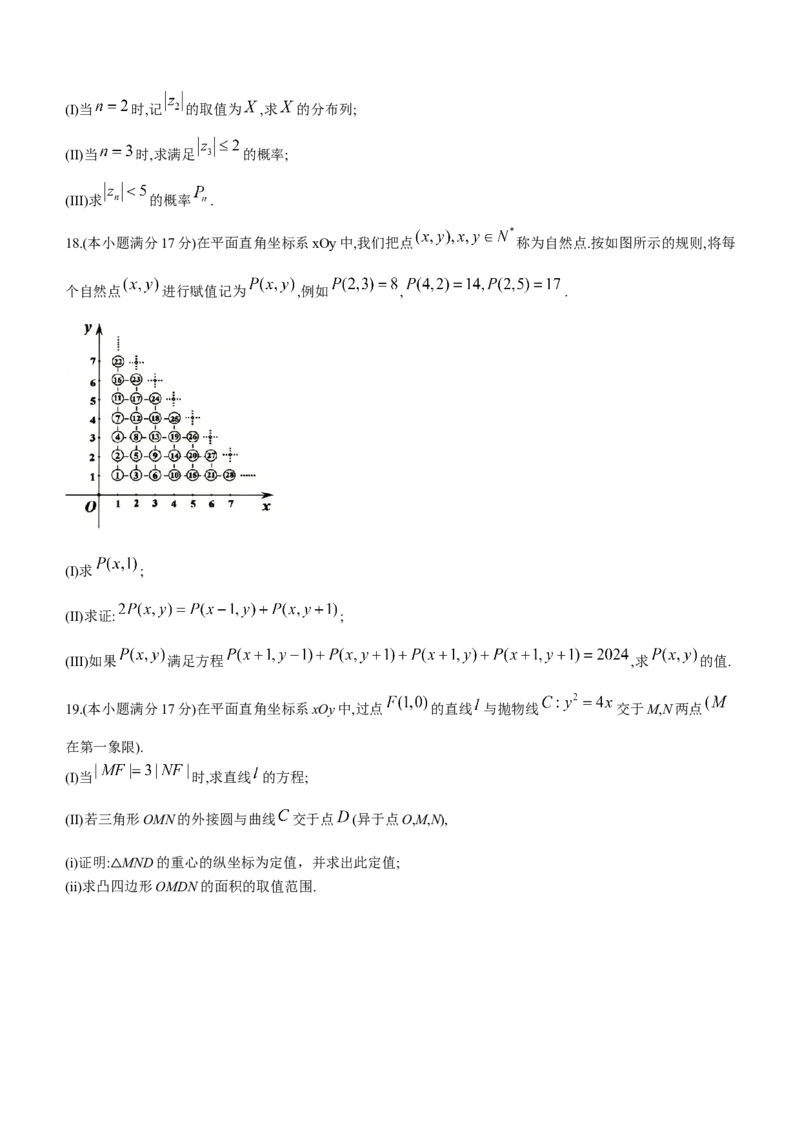
15.(本小题满分13分)如图,斜三棱柱 的底面是直角三角形, ,点 在底面ABC内的
射影恰好是BC的中点,且 .
(I)求证:平面 平面 ;
(II)若斜棱柱的高为 ,求平面 与平面 夹角的余弦值.
16.(本小题满分15分)己知函数 ,其中 .
(I)若曲线 在 处的切线在两坐标轴上的截距相等,求 的值;
(II)是否存在实数 ,使得 在 上的最大值是-3?若存在,求出 的值;若不存在,说明理由.
17.(本小题满分15分)记复数的一个构造:从数集 中随机取出2个不同的数作为复数的实部和虚部.重
复 次这样的构造,可得到 个复数,将它们的乘积记为 .
已知复数具有运算性质: ,其中 .(I)当 时,记 的取值为 ,求 的分布列;
(II)当 时,求满足 的概率;
(III)求 的概率 .
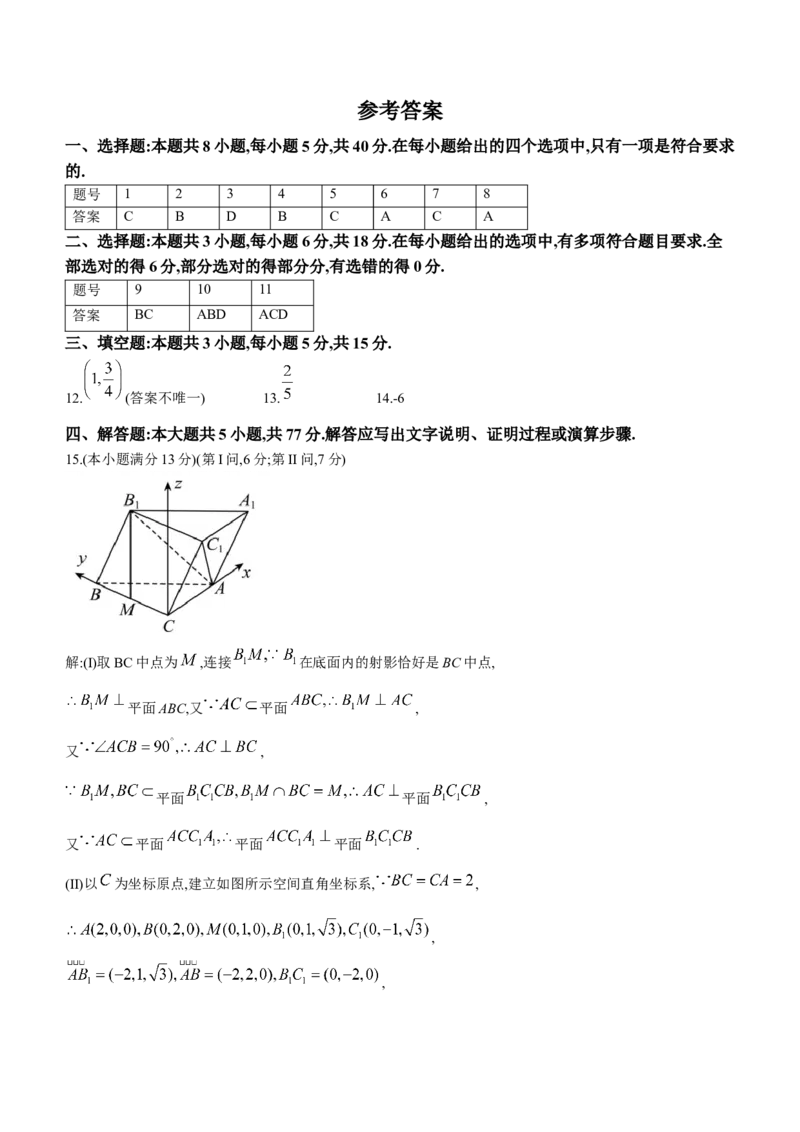
18.(本小题满分17分)在平面直角坐标系xOy中,我们把点 称为自然点.按如图所示的规则,将每
个自然点 进行赋值记为 ,例如 , .
(I)求 ;
(II)求证: ;
(III)如果 满足方程 ,求 的值.
19.(本小题满分17分)在平面直角坐标系xOy中,过点 的直线 与抛物线 交于M,N两点
在第一象限).
(I)当 时,求直线 的方程;
(II)若三角形OMN的外接圆与曲线 交于点 (异于点O,M,N),
(i)证明: MND的重心的纵坐标为定值,并求出此定值;
(ii)求凸四边形OMDN的面积的取值范围.
△参考答案
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求
的.
题号 1 2 3 4 5 6 7 8
答案 C B D B C A C A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
部选对的得6分,部分选对的得部分分,有选错的得0分.
题号 9 10 11
答案 BC ABD ACD
三、填空题:本题共3小题,每小题5分,共15分.
12. (答案不唯一) 13. 14.-6
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)(第I问,6分;第II问,7分)
解:(I)取BC中点为 ,连接 在底面内的射影恰好是BC中点,
平面ABC,又 平面 ,
又 ,
平面 平面 ,
又 平面 平面 平面 .
(II)以 为坐标原点,建立如图所示空间直角坐标系, ,
,
,设平面 的法向量为 ,
则有 ,令 ,则 ,
设平面 的法向量为 ,
则有 ,令 则 ,
,
平面 与平面 夹角的余弦值为 .
16.(本小题满分15分)(第I问,6分;第II问,9分)
(I) ,则 ,
故曲线 在 处的切线为 ,
即 ,
当 时,此时切线为 ,不符合要求
当 时,令 ,有 ,
令 ,有 ,故 ,即 ,故
(II) ,
①当 时, 在 上单调递增,
的最大值是 ,解得 ,舍去;
②当 时,由 ,得 ,当 ,即 时, 时, 时, ,
的单调递增区间是 ,单调递减区间是 ,
又 在 上的最大值为 ;
当 ,即 时, 在 上单调递增, ,
解得 ,舍去.综上,存在 符合题意,此时
17.(本小题满分15分)(第I问,6分;第II问,4分;第III问,5分)
(I)由题意可知,可构成的复数为 ,
的可能取值为 ,
,
,
所以分布列为:
X 1 2 3 4
(II)共有 种,
满足 的情况有:
①3个复数的模长均为1,共有 种;
②3个复数中,2个模长均为1,1个模长为 或者2,共有 种;所以 .
(III)当 或2时,显然都满足,此时 ;
当 时,满足 共有三种情况:
① 个复数的模长均为1,则共有 ;
② 个复数的模长为1,剩余1个模长为 或者2,则共有 ;
③ 个复数的模长为1,剩余2个模长为 或者2,则共有 .
故 ,
此时当 均成立.
所以 .
18.(本小题满分17分)(第I问,4分;第II问,7分;第III问,6分)
解:(I)根据图形可知 ,
(II)固定 ,则 为一个高阶等差数列,且满足
所以
所以 , ,所以P(x+1,y-1)+P(x,y+1)+P(x+1,y)+P(x+1,y+1)=2024
等价于 ,
等价于
即 ,
化简得 ,
由于 增大, 也增大,
当 时, ,
当 时, ,
故当 时, ,即
19.(本小题满分17分)(第I问,4分;第II问,5分;第III问,8分)
解:(I)设直线
联立 ,消去 ,得 ,
所以 ,
,则
,则 ,又由题意 ,
直线的方程是 ;
(II)(i)方法1:设
因为O,M,D,N四点共圆,设该圆的方程为 ,联立 ,消去 ,得 ,
即 ,
所以 即为关于 的方程 的3个根,
则 ,
因为 ,
由 的系数对应相等得, ,所以 的重心的纵坐标为0.
方法2:设 ,则 ,
因为O,M,C,N四点共圆,所以 ,即 ,
化简可得: ,
所以 的重心的纵坐标为0.
(ii)记 的面积分别为 ,由已知得直线MN的斜率不为0设直线 ,联立
,消去 ,得 ,所以 ,
所以 ,
由(i)得, ,
所以 ,即 ,
因为 ,点 到直线MN的距离 ,
所以 ,
所以
在第一象限,即 ,
依次连接O,M,D,N构成凸四边形OMDN,所以 ,即 ,
又因为 ,即 ,即 ,
所以 ,即 ,即 ,
所以 ,
设 ,则 ,
令 ,则 ,
因为 ,所以 ,所以 在区间 上单调递增,所以
,
所以 的取值范围为 .