文档内容
2023—2024 学年第二学期浙江省 9+1 高中联盟 3 月高考模拟卷
数学
考生须知:
1.本卷满分150分,考试时间120分钟;
2.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答
题纸规定的位置上;
3.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试
卷上的作答一律无效;
4.选择题一律使用 2B铅笔填涂答案,非选择题一律用 0.5毫米黑色字迹中性笔写在答题纸
上相应区域内;
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.)
1.已知全集 ,则 (
)
A. B. C. D.
2.若复数 的实部大于0,且 ,则 ( )
A. B. C. D.
3.已知向量 是平面上两个不共线的单位向量,且 ,
则( )
A. 三点共线 B. 三点共线
C. 三点共线 D. 三点共线
4.已知数列 满足: ,且数列 为等差数列,则 ( )
A.10 B.40 C.100 D.103
5.如图,已知长方体 的体积为 是棱 的中点,平面 将长方体分割成两
部分,则体积较小的一部分的体积为( )A. B. C. D.
6 . 已 知 椭 圆 , 直 线 与 交 于 两 点 , 且
.则椭圆 的离心率是( )
A. B. C. D.
7.某羽毛球俱乐部,安排男女选手各6名参加三场双打表演赛(一场为男双,一场为女双,一场为男女混
双),每名选手只参加1场表演赛,则所有不同的安排方法有( )
A.2025种 B.4050种 C.8100种 D.16200种
8.设函数 .若实数 使得 对任意 恒成立,
则 ( )
A. B.0 C.1 D.
二、多项选择题(本题共 3小题,每小题6分,共18分。在每小题给出的选项中,有多项符
合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分)
9.为了得到函数 的图象,只要把函数 图象上所有的点( )
A.向左平移 个单位长度 B.向右平移 个单位
长度
C.向左平移 个单位长度 D.向右平移 个单位长度
10.高考数学试题的第二部分为多选题,共三个题每个题有 4个选项,其中有2个或3个是正确选项,全
部选对者得6分,部分选对的得2分,有选错的得0分.小明对其中的一道题完全不会,该题有两个选项正确的概率是 ,记 为小明随机选择1个选项的得分,记 为小明随机选择2个选项的得分.则
A. B.
C. D.
11.对于 满足 ,且对于 .恒有
.则( )
A. B. C. D .
三、填空题(本题共3小题,每小题5分,共15分。请把答案直接填写在答题卡相应位置
上)
12.已知 .若 ,则
________.
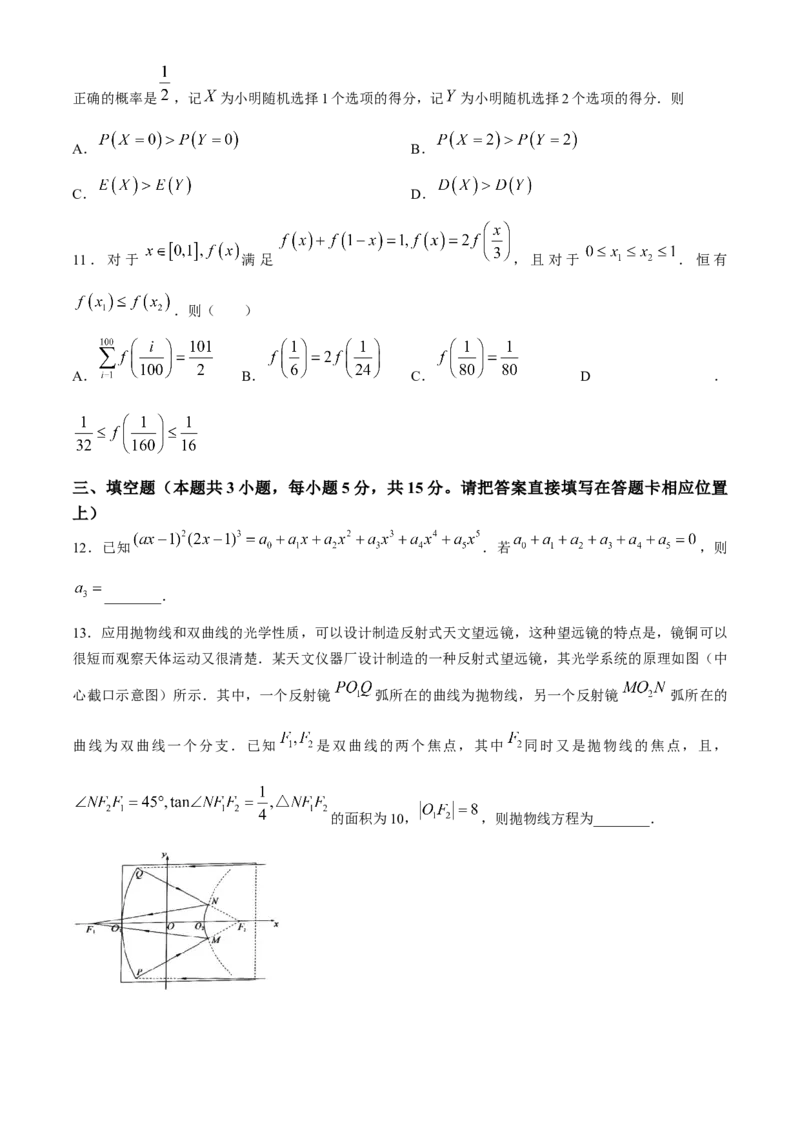
13.应用抛物线和双曲线的光学性质,可以设计制造反射式天文望远镜,这种望远镜的特点是,镜铜可以
很短而观察天体运动又很清楚.某天文仪器厂设计制造的一种反射式望远镜,其光学系统的原理如图(中
心截口示意图)所示.其中,一个反射镜 弧所在的曲线为抛物线,另一个反射镜 弧所在的
曲线为双曲线一个分支.已知 是双曲线的两个焦点,其中 同时又是抛物线的焦点,且,
的面积为10, ,则抛物线方程为________.14.函数 的最小值是________.
四、解答题(本大题共5小题,共计77分.请在答题纸指定区域内作答,解答应写出文字说
明,证明过程或演算步骤.)
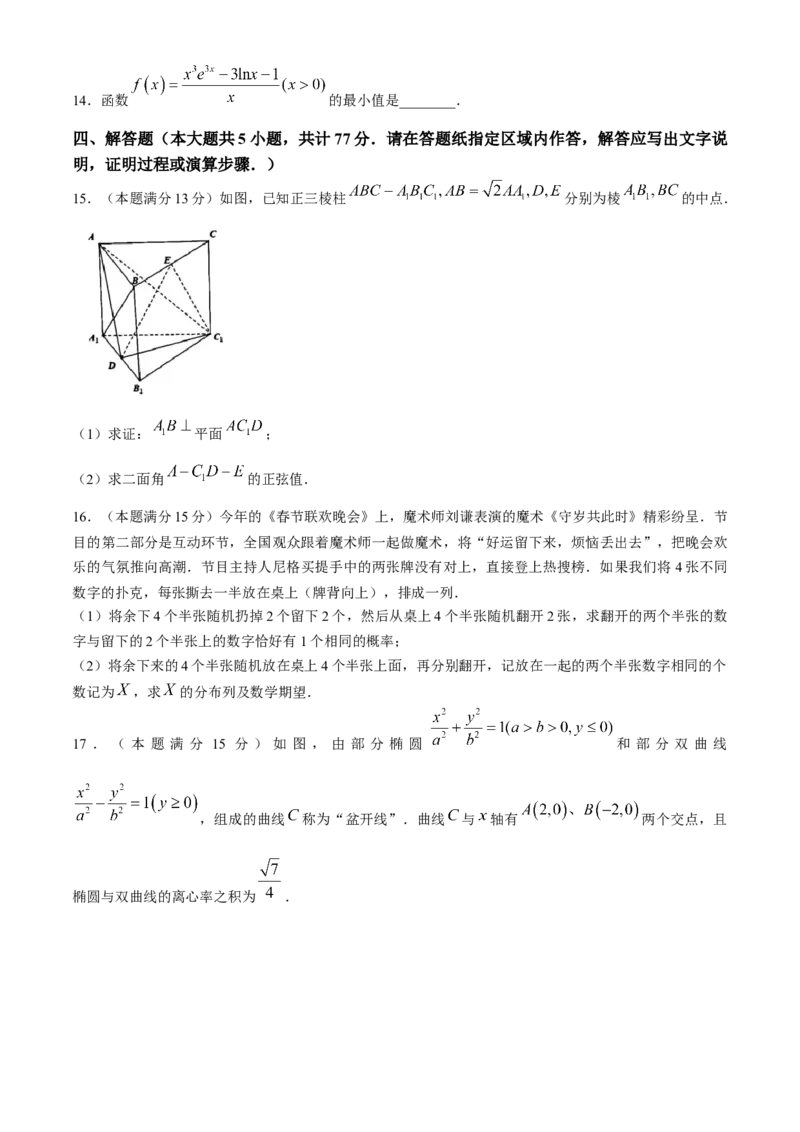
15.(本题满分13分)如图,已知正三棱柱 分别为棱 的中点.
(1)求证: 平面 ;
(2)求二面角 的正弦值.
16.(本题满分15分)今年的《春节联欢晚会》上,魔术师刘谦表演的魔术《守岁共此时》精彩纷呈.节
目的第二部分是互动环节,全国观众跟着魔术师一起做魔术,将“好运留下来,烦恼丢出去”,把晚会欢
乐的气氛推向高潮.节目主持人尼格买提手中的两张牌没有对上,直接登上热搜榜.如果我们将 4张不同
数字的扑克,每张撕去一半放在桌上(牌背向上),排成一列.
(1)将余下4个半张随机扔掉2个留下2个,然后从桌上4个半张随机翻开2张,求翻开的两个半张的数
字与留下的2个半张上的数字恰好有1个相同的概率;
(2)将余下来的4个半张随机放在桌上4个半张上面,再分别翻开,记放在一起的两个半张数字相同的个
数记为 ,求 的分布列及数学期望.
17 . ( 本 题 满 分 15 分 ) 如 图 , 由 部 分 椭 圆 和 部 分 双 曲 线
,组成的曲线 称为“盆开线”.曲线 与 轴有 两个交点,且
椭圆与双曲线的离心率之积为 .(1)设过点 的直线 与 相切于点 ,求点 的坐标及直线 的方程;
(2)过 的直线 与 相交于点 三点,求证: .
18.(本题满分17分)已知函数 .
(1)如果1和 是 的两个极值点,且 的极大值为3,求 的极小值;
(2)当 时,讨论 的单调性;
(3)当 时,且函数 在区间 上最大值为2,最小值为 .求 的值.
19 . ( 本 题 满 分 17 分 ) 已 知 实 数 , 定 义 数 列 如 下 : 如 果
, ,则 .
(1)求 和 (用 表示);
(2)令 ,证明: ;
(3)若 ,证明:对于任意正整数 ,存在正整数 ,使得 .2023-2024 学年第二学期浙江省 9+1 高中联盟 3 月高考模拟卷
数学参考答案
一、选择题(本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一项是
符合题目要求的.)
1.【答案】C
【解析】因为集合 .
2.【答案】D
【 解 析 】 令 , 代 入 , 得 . 解 得 :
.
3.【答案】C
【解析】因为 ,所以 三点共
线.
4.【答案】D
【解析】设数列 的公差为 ,则 ,所以 .
5.【答案】A
【解析】设长方体的长、宽、高分别为 ,易知平面 与 交于中点
.
6.【答案】B
【解析】设 ,记 ,由题意可知, 中点 是直线 与直线
的交点,即 .另一方面,联立 ,得 .
由韦达定理得: ,解得 ,故离心率 .7.【答案】B
【解析】先填考虑两对混双的组合有 种不同的方法,余下4名男选手和4名女选手各有3种不同
的配对方法组成两对男双组合,两对女双组合,故共有 .
8.【答案】C
【解析】由条件可知: 对任意的 恒成立,
.
.
,由 知 或 .
若 时,则由 知 ,这与 矛盾!
若 ,则 (舍去), ,解得 ,所以, .
二、多项选择题(本题共 3小题,每小题6分,共18分。在每小题给出的选项中,有多项符
合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分)
9.【答案】AD
【解析】 ,故答案A正确,B错误;
又由 ,故答案C错误,正确.
10.【答案】BC
【解析】 的分布列
0 2
由此可得
的分布列
0 2 6由此可得 .
从而可知,BC正确.
11.【答案】ABD
【解析】令 代入 及 ,得 ,所
以 , 令 代 入 , 得
,答案 A 正确;由 ,得 ,进而得,
,所以,
BD正确,C错误.
三、填空题(本题共3小题,每小题5分,共15分。请把答案直接填写在答题卡相应位置
上)
12.【答案】38
【解析】由题设可得 .
13.【答案】
【解析】不妨设 .由 ,所以,
,又 .即 ,故抛物线方程为
.
14.【答案】3
【解析】 ,令 ,显然 在上单调增 ,存在 ,
使 ,且 ,故当 时, ,即
,所以 在区间 单调减,当 时, ,即 ,所以
在区间 单调增,所以 .
四、解答题(本大题共5小题,共计77分.请在答题纸指定区域内作答,解答应写出文字说
明,证明过程或演算步骤.)
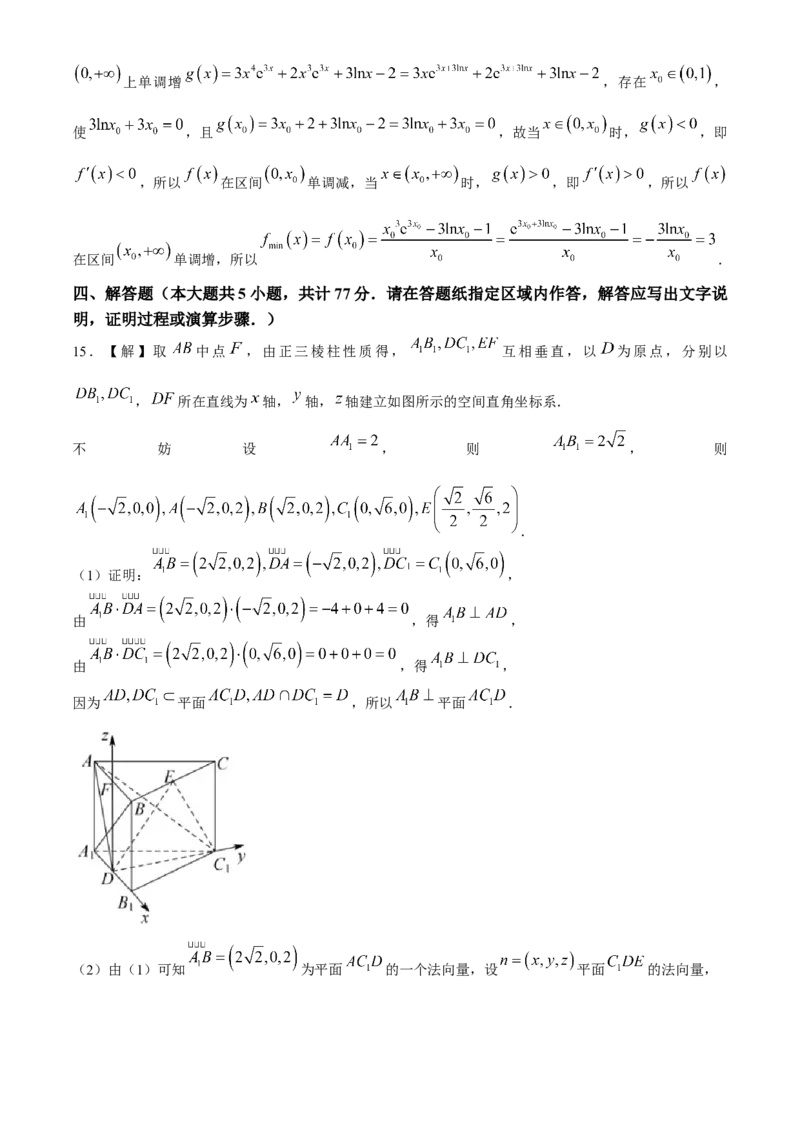
15.【解】取 中点 ,由正三棱柱性质得, 互相垂直,以 为原点,分别以
, 所在直线为 轴, 轴, 轴建立如图所示的空间直角坐标系.
不 妨 设 , 则 , 则
.
(1)证明: ,
由 ,得 ,
由 ,得 ,
因为 平面 ,所以 平面 .
(2)由(1)可知 为平面 的一个法向量,设 平面 的法向量,则 ,
令 ,得面 的一个法向量为 ,
设二面角 的值为 ,
则 ,所以,二面角 的正弦值为 .
16.【解】(1)设翻开的两个半张的数字与留下的2个半张上的数字恰好有1个相同的事件设为 ,则
.
答:翻开的两个半张的数字与留下的2个半张上的数字恰好有1个相同的概率为 .
(2) 的分布列
0 1 2 4
.
17.【解】由题设可得 ,
故椭圆方程为: ,双曲线方程为 .
(1)由图可知,切点 在双曲线 上.
设 ,则切线 的方程为: ,
因为直线 过点 ,所以, ,
将 代入 ,得 ,所以, ,直线 的方程为: .
(2)由题意得 方程为: ,
联立 ,整理得: ,
解得: ,或 ,即 .
联立 ,整理得: ,
解得: ,或 ,即 .
,
所以, ,所以 .
18.【解】(1) ,因为1和 是 的两个极值点,所以,1和 是方程
的两根,故 ,即 .
因为 时, 时, ,
所以 在区间 上单调增,在区间 上单调减,
所以 ,得 ,
.
(2)当 时, .
令 ,得 ,或 .若 ,则当 时, ;当 时, .故 在
区间 单调递增,在 上单调递减;
若 在区间 单调递增;
若 ,则当 时, ;当 时, .故 在
区间 单调递增,在 上单调递减.
( 3 ) 当 时 , , 由 题 意 得 : , 即
,①
,即 ,②
由①、②可知, .③
因 为 , , ,
,所以, 有两个实数根 ,且 ,
当 时, ,当 时, ,故 是 的极大值点, 是
的极小值点.
由题意得:
两式同向相加得: ,④
注意到, ,
代入④得: ,由 ③ 可 知 , , 所 以 , 所 以
,
当且仅当 时成立.
所以 ,从而 .
19.【解】(1)因为 ,所以 ;
因为 ,所以 .
(2)由数列 定义得: ;所以 .
而 ,
所以 .
(3)当 ,由(2)可知, 无上界,故对任意 ,存在 ,使得 .
设 是满足 的最小正整数.下面证明 .
①若 是偶数,设 ,
则 ,于是 .
因为 ,所以 .
②若 是奇数,设 ,
则 .
所以 .
综上所述,对于任意正整数 ,存在正整数 ,使得 .