浙江省2024年普通高考适应性测试数学试题(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_浙江省2024年普通高考适应性测试数学试题

参照机密级管理★启用前 浙江省 2024 年普通高考适应性测试 数 学 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标 号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将 答案写在答题卡上。写在本试卷上无效。 3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共 8小题，每小题5分，共 40分．在每小题给出的四个选项中， 只有一项是符合题目要求的． 1．ABC中，AB5，BC6，CA7，则ABC的面积为（ ） A．6 6 B．6 3 C．3 6 D．3 3 2．已知m,n为两条不同的直线，,为两个不同的平面，对于下列四个命题： ①m,n,m//,n////；②n//m,nm//； ③//,m,nm//n；④m//,nm//n． 其中正确命题的个数有（ ） A．0个 B．1个 C．2个 D．3个 3．下列说法正确的是（ ）  1 A．若随机变量B12, ，则D()3  4 B．若随机变量 N  2,2 ，且P40.8，则P240.4 C．一组数据11，12，12，13，14，15，16，18，20，22的第80百分位数为19 1 2 1 D．若PAB ，PA ，PB ，则事件A与事件B相互独立 9 3 3  4．设a是非零向量，是非零实数，则下列结论中正确的是（ ）     A．a的方向a的方向相反 B． a  a     C．a与2a 方向相同 D．a  a 1  5．已知sincos ，0，则 2sin( )的值为 5 4 1 7 1 7 A． B． C． D． 5 5 5 5 6．在某班进行的演讲比赛中，共有6位选手参加，其中2位女生，4位男生，如果2位女生不 数学试题第 1 页（共 4 页） {#{QQABKQSUogAgABIAAQgCQw24CEAQkAECCCoOAEAEMAIACBFABAA=}#}能连续出场，且女生不能排在第一个和最后，则出场顺序的排法种数为（ ） A．120 B．144 C．480 D．90 4 x2 y2 7．已知过原点且斜率为 的直线l交双曲线  1(a0,b0)于M ，N 两点，点F 是双曲线 3 a2 b2   的一个焦点，若MFNF 0，则双曲线的离心率为（ ） A． 5 B． 3 C．2 D． 2 a 8．已知数列a 满足a 1，且a  n ，nN*，则（ ） n 1 n1 a21 n  1 1   1 1  A． a  ,  B．a  ,  50 12 11 50 11 10  1 1 1 1 C．a  ,  D．a  ,  50 10 9 50 9 8 二、选择题：本题共 3 小题，每小题 6 分，共 18 分．在每小题给出的选项中，有 多项符合题目要求．全部选对的得 6分，部分选对的得部分分，有选错的得 0分．  π 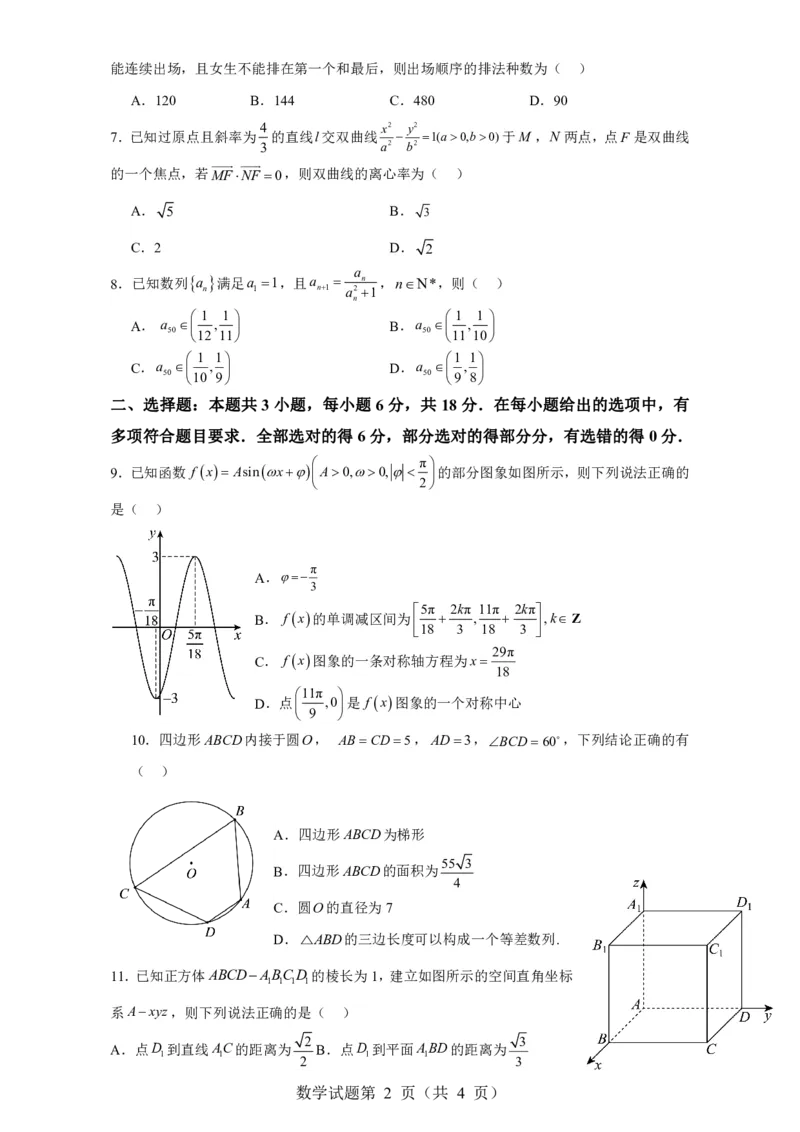9．已知函数 f x Asinx A0,0, 的部分图象如图所示，则下列说法正确的  2 是（ ） π A． 3 5π 2kπ 11π 2kπ B． f x的单调减区间为   ,   ,k Z 18 3 18 3  29π C． f x图象的一条对称轴方程为x 18 11π  D．点 ,0是 f x图象的一个对称中心  9  10．四边形ABCD内接于圆O， ABCD5，AD3，BCD60，下列结论正确的有 （ ） A．四边形ABCD为梯形 55 3 B．四边形ABCD的面积为 4 C．圆O的直径为7 D．△ABD的三边长度可以构成一个等差数列. 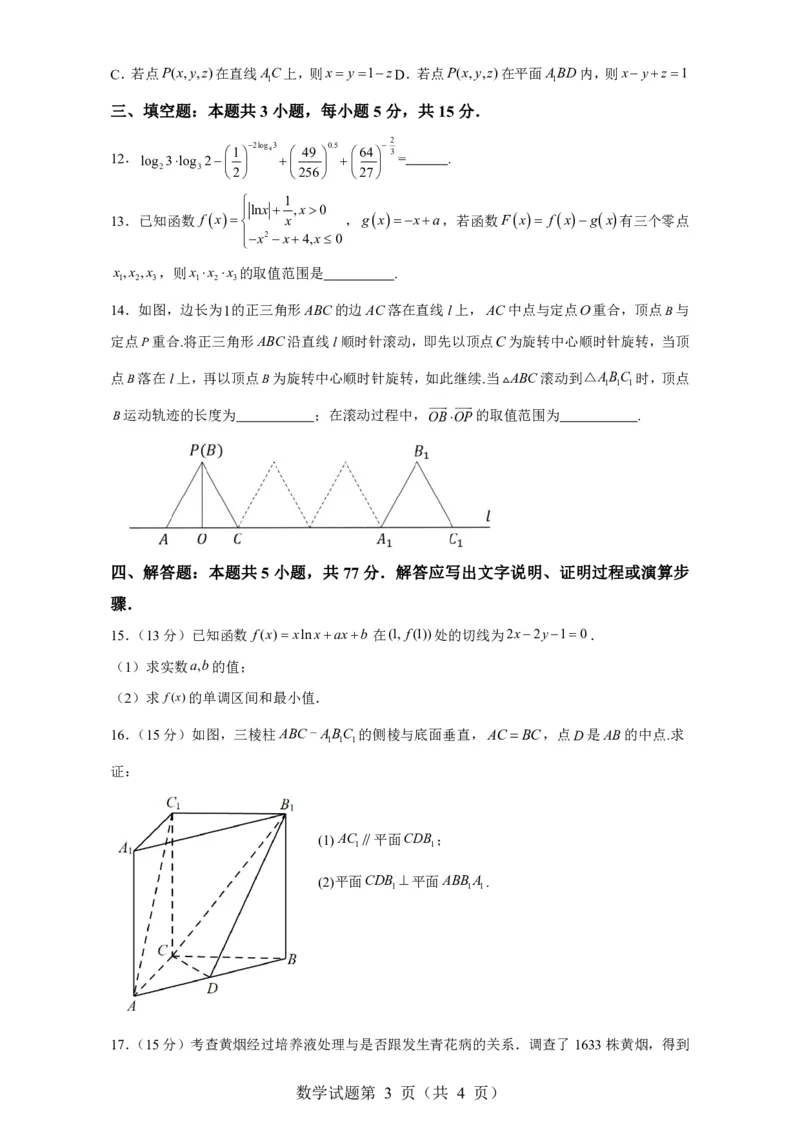11．已知正方体ABCDABCD 的棱长为1，建立如图所示的空间直角坐标 1 1 1 1 系Axyz，则下列说法正确的是（ ） 2 3 A．点D 到直线AC的距离为 B．点D 到平面ABD的距离为 1 1 1 1 2 3 数学试题第 2 页（共 4 页） {#{QQABKQSUogAgABIAAQgCQw24CEAQkAECCCoOAEAEMAIACBFABAA=}#}C．若点P(x,y,z)在直线AC上，则x y1zD．若点P(x,y,z)在平面ABD内，则xyz1 1 1 三、填空题：本题共 3小题，每小题 5分，共 15分． 2 12． log 3log 2   1  2log43    49   0.5    64   3 = . 2 3 2 256 27  1 lnx  ,x0 13．已知函数 f x x ，gxxa，若函数Fx fxgx有三个零点  x2x4,x0 x,x ,x ，则x x x 的取值范围是 . 1 2 3 1 2 3 14．如图，边长为1的正三角形ABC的边AC落在直线l上，AC中点与定点O重合，顶点B与 定点P重合.将正三角形ABC沿直线l顺时针滚动，即先以顶点C为旋转中心顺时针旋转，当顶 点B落在l上，再以顶点B为旋转中心顺时针旋转，如此继续.当ABC滚动到△ABC 时，顶点 1 1 1   B运动轨迹的长度为 ；在滚动过程中，OBOP的取值范围为 . 四、解答题：本题共 5 小题，共 77分．解答应写出文字说明、证明过程或演算步 骤． 15．（13分）已知函数 f(x)xlnxaxb 在(1, f(1))处的切线为2x2y10． （1）求实数a,b的值； （2）求 f(x)的单调区间和最小值． 16．（15分）如图，三棱柱ABC-ABC 的侧棱与底面垂直，ACBC，点D是AB的中点.求 1 1 1 证： (1)AC 平面CDB ； 1 1 (2)平面CDB 平面ABBA. 1 1 1 17．（15分）考查黄烟经过培养液处理与是否跟发生青花病的关系．调查了1633株黄烟，得到 数学试题第 3 页（共 4 页） {#{QQABKQSUogAgABIAAQgCQw24CEAQkAECCCoOAEAEMAIACBFABAA=}#}如表中数据，请根据数据作统计分析： 培养液处理 未处理 合计 青花病 30 224 254 无青花病 24 1355 1379 合计 54 1579 1633 P(K2 k) 0.05 0.01 0.005 0.001 k 3.841 6.635 7.879 10.83 n(adbc)2 附：K2  (ab)(cd)(ac)(bd) 18．（17分）已知函数 f xaxlnx3. （1）当a1 时，求函数 f x在点1,2处的切线方程； （2）若函数 f x在x  e4,e  上的图象与直线y=t(0＃t 1)总有两个不同交点，求实数a的 取值范围． 19．（17分）同余定理是数论中的重要内容．同余的定义为：设a，bZ，mN*且m  1．若 m(ab)则称a与b关于模m同余，记作ab（modm）（“|”为整除符号）． (1)解同余方程x2x0（mod3）； (2)设（1）中方程的所有正根构成数列a ，其中a a a a ． n 1 2 3 n ①若b a a （nN*），数列b 的前n项和为S ，求S ； n n1 n n n 2024 ②若c tana tana （nN*），求数列c 的前n项和T ． n 2n1 2n1 n n 数学试题第 4 页（共 4 页） {#{QQABKQSUogAgABIAAQgCQw24CEAQkAECCCoOAEAEMAIACBFABAA=}#}