文档内容
2023 学年第二学期浙江省名校协作体试题
高二年级数学学科
考生须知:
1.本卷满分 150分,考试时间 120分钟.
2.答题前,在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号.
3.所有答案必须写在答题卷上,写在试卷上无效.
4.考试结束后,只需上交答题卷.
选择题部分
一、选择题:本题 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求.
1.抛物线x2 =4y的准线方程为( )
A.x=−1 B.x=−2 C.y =−1 D.y =−2
5 5 17
2.数列1, , , ,…的通项公式可能是( )
3 2 5
n2 +1 n+1 n2 2n−1
A.a = B.a = C.a = D.a =
n n+1 n n2 +1 n 2n−1 n n2
3.已知直线l :mx+ y+1=0,l :3x+( m+2 ) y+3m=0,若l ∥l ,则m的值为( )
1 2 1 2
A.1 B.-3 C.1或-3 D.-1或3
4.已知两条直线m,n,两个平面α,β,则下列命题正确的是( )
A.若m∥n且n⊂α,则m∥α B.若m∥α且n⊂α,则m∥n
C.若m⊥α且n⊂α,则m⊥n D.若α⊥β且m⊂α,则m⊥β
5.已知点P (−4,2 )和圆Q:( x−4 )2 +( y−2 )2 =16,则以PQ为直径的圆与圆Q的公共弦长是( )
A.2 5 B.2 3 C.4 5 D.4 3
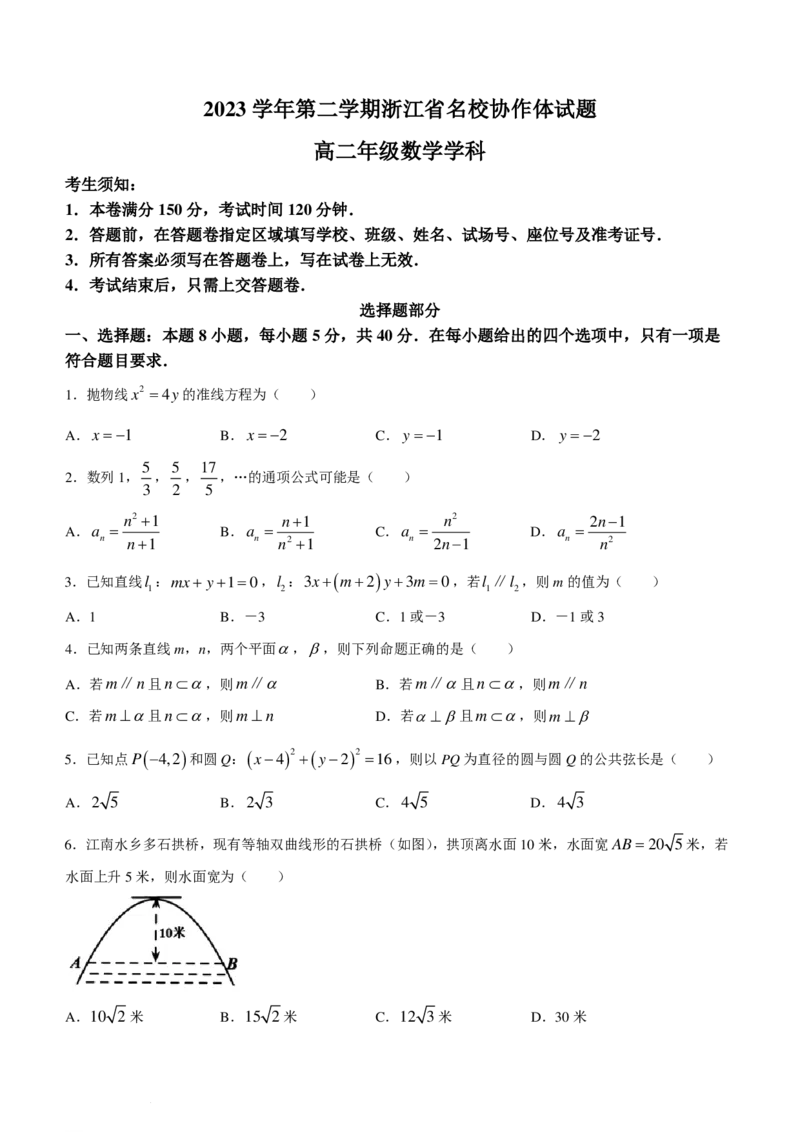
6.江南水乡多石拱桥,现有等轴双曲线形的石拱桥(如图),拱顶离水面10米,水面宽AB=20 5米,若
水面上升5米,则水面宽为( )
A.10 2 米 B.15 2米 C.12 3米 D.30米
学科网(北京)股份有限公司1
7.在正三棱台ABC−ABC 中,AB = AA = AB=3,ABAB =O,则异面直线OC与BC 所成角
1 1 1 1 1 1 2 1 1 1
的余弦值是( )
1 2 3 2
A. B. C. D.
3 3 3 3
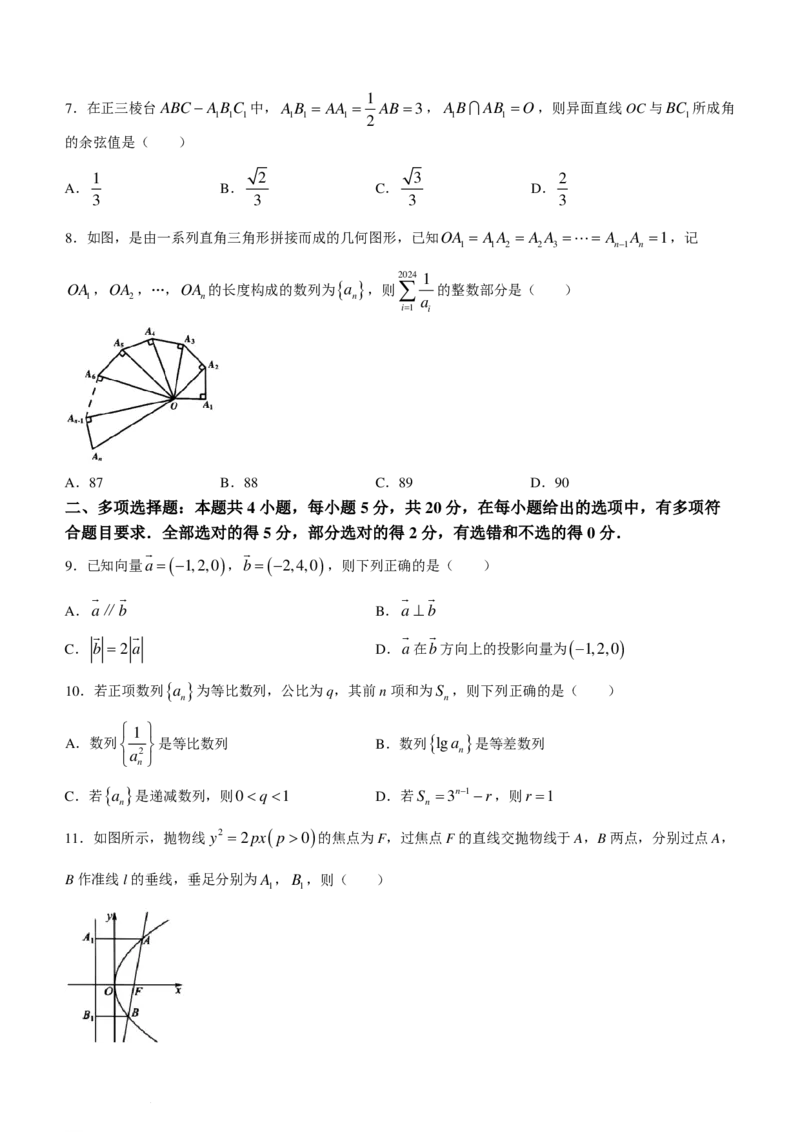
8.如图,是由一系列直角三角形拼接而成的几何图形,已知OA = AA = A A =⋅⋅⋅= A A =1,记
1 1 2 2 3 n−1 n
2024 1
OA ,OA ,…,OA 的长度构成的数列为{ a },则∑ 的整数部分是( )
1 2 n n a
i=1 i
A.87 B.88 C.89 D.90
二、多项选择题:本题共 4小题,每小题 5分,共 20分,在每小题给出的选项中,有多项符
合题目要求.全部选对的得 5分,部分选对的得 2分,有选错和不选的得 0分.
9.已知向量a=(−1,2,0 ),b=(−2,4,0 ),则下列正确的是( )
A.a∥b B.a ⊥b
C. b =2 a D.a在b方向上的投影向量为(−1,2,0 )
10.若正项数列{ a }为等比数列,公比为q,其前n项和为S ,则下列正确的是( )
n n
1
A.数列 是等比数列 B.数列{ lga }是等差数列
a2
n
n
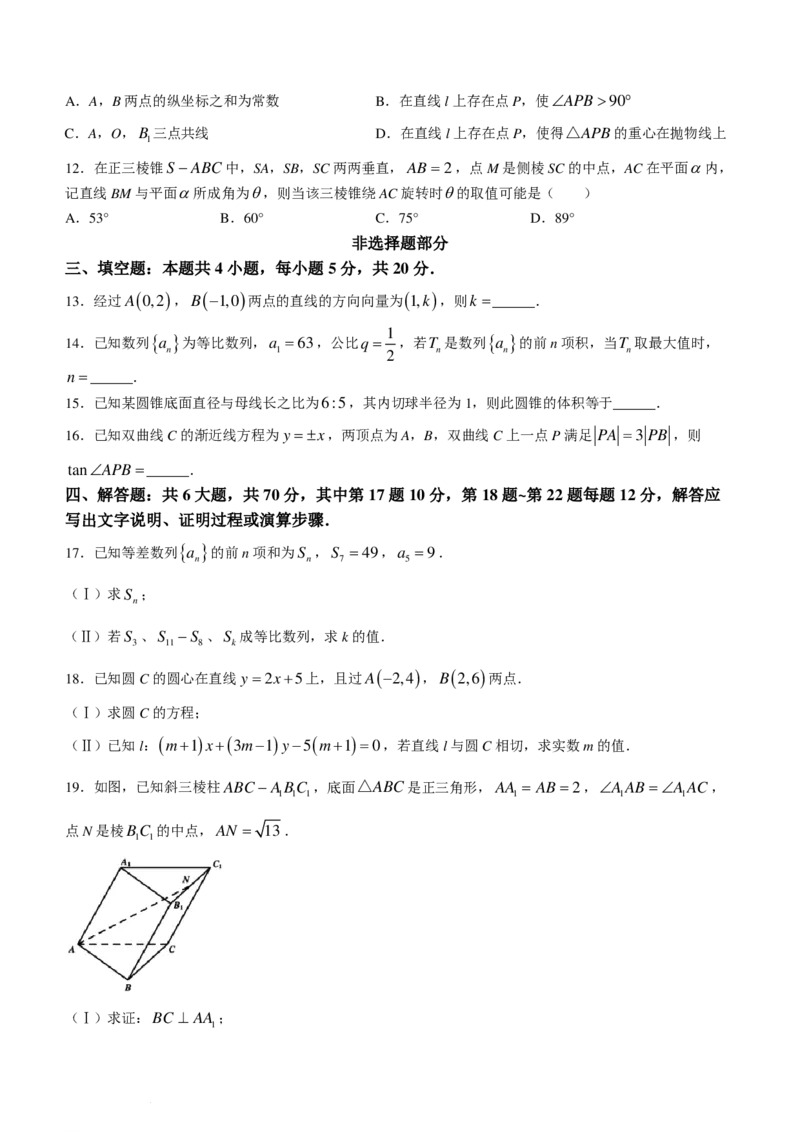
C.若{ a }是递减数列,则00 )的焦点为F,过焦点F的直线交抛物线于A,B两点,分别过点A,
B作准线l的垂线,垂足分别为A,B ,则( )
1 1
学科网(北京)股份有限公司A.A,B两点的纵坐标之和为常数 B.在直线l上存在点P,使∠APB>90°
C.A,O,B 三点共线 D.在直线l上存在点P,使得△APB的重心在抛物线上
1
12.在正三棱锥S−ABC中,SA,SB,SC两两垂直,AB =2,点M是侧棱SC的中点,AC在平面α内,
记直线BM与平面α所成角为θ,则当该三棱锥绕AC旋转时θ的取值可能是( )
A.53° B.60° C.75° D.89°
非选择题部分
三、填空题:本题共 4小题,每小题 5分,共 20分.
13.经过A ( 0,2 ),B (−1,0 )两点的直线的方向向量为( 1,k ),则k =______.
1
14.已知数列{ a }为等比数列,a =63,公比q= ,若T 是数列{ a }的前n项积,当T 取最大值时,
n 1 2 n n n
n=______.
15.已知某圆锥底面直径与母线长之比为6:5,其内切球半径为1,则此圆锥的体积等于______.
16.已知双曲线C的渐近线方程为y =±x,两顶点为A,B,双曲线C上一点P满足 PA =3 PB ,则
tan∠APB=______.
四、解答题:共 6大题,共 70分,其中第 17题 10分,第 18题~第22题每题 12分,解答应
写出文字说明、证明过程或演算步骤.
17.已知等差数列{ a }的前n项和为S ,S =49,a =9.
n n 7 5
(Ⅰ)求S ;
n
(Ⅱ)若S 、S −S 、S 成等比数列,求k的值.
3 11 8 k
18.已知圆C的圆心在直线y =2x+5上,且过A (−2,4 ),B ( 2,6 )两点.
(Ⅰ)求圆C的方程;
(Ⅱ)已知l:( m+1 ) x+( 3m−1 ) y−5 ( m+1 )=0,若直线l与圆C相切,求实数m的值.
19.如图,已知斜三棱柱ABC−ABC ,底面△ABC是正三角形,AA = AB=2,∠AAB=∠AAC,
1 1 1 1 1 1
点N是棱BC 的中点,AN = 13.
1 1
(Ⅰ)求证:BC ⊥ AA ;
1
学科网(北京)股份有限公司(Ⅱ)求平面AAN与平面ANB的夹角的余弦值.
1
5
20.已知点F为抛物线C:y2 =2px ( 0< p<1 )的焦点,点A ( x ,1 )在抛物线C上,且 AF = .
0
4
(Ⅰ)求抛物线C的方程;
1
(Ⅱ)若直线l与抛物线C交于M,N两点,设直线AM,AN的斜率分别为k ,k ,且k ⋅k =− ,求
1 2 1 2 2
证:直线l过定点.
21.已知数列{ a }满足a =2, a n+1 −1 = pa +(−1 )p( n∈N* ) .
n 1 a n
n
{ }
(Ⅰ)若 p =0,求数列 3n⋅a 的前n项和S ;
n n
1 1
(Ⅱ)若 p=1,设数列 的前n项和为T ,求证: ≤T <1.
a n 2 n
n
7 x2 y2 x2 y2
22.已知离心率为 的双曲线C : − =1 ( a>0,b>0 )过椭圆C : + =1的左,右顶点A,
2 1 a2 b2 2 4 3
B.
(Ⅰ)求双曲线C 的方程;
1
(Ⅱ)P ( x ,y )( x >0,y >0 )是双曲线C 上一点,直线AP,BP与椭圆C 分别交于D,E,设直线DE
0 0 0 0 1 2
与x轴交于Q ( x ,0 ) ,且x =λ2x 0<λ< 1 ,记△BDP与△ABD的外接圆的面积分别为S ,S ,
Q Q 0 2 1 2
S
求 1 的取值范围.
S
2
2023 学年第二学期浙江省名校协作体联考参考答案
高二年级数学学科
首命题:柯桥中学 次命题兼审校:丽水中学 审核:瑞安中学
一、单选题:本题共 8小题,每小题 5分,共 40分.
1.C 2.A 3.B 4.C 5.D 6.D 7.B 8.B
8.解析:由题意知,OA = AA = A A =⋅⋅⋅= A A =1且△OAA ,△OA A ,…,△OA A 都是直
1 1 2 2 3 n−1 n 1 2 2 3 n−1 n
角三角形,所以a =1,且a 2 =a2 +1,所以数列 { a 2 } 是以1为首项,1为公差的等差数列,所以
1 n n−1 n
学科网(北京)股份有限公司2024 1 1 1 1
a 2 =1+( n−1 )×1=n∑ = + ++ ,
n a 1 2 2024
i=1 i
1 1 1 1 2 2
∵ + ++ < + ++ =2 2024−1<2 2025−1=89,
1 2 2024 1 1+ 2 2023+ 2024
1 1 1 2 2 2
∵ + ++ > + ++ =2 2025−2=88,
1 2 2024 1+ 2 2+ 3 2024+ 2025
1 1 1
即88< + ++ <89,
1 2 2024
所以所求整数部分都是88,故选:B.
二、多选题:本题共 4小题,每小题 5分,共 20分.
9.ACD 10.ABC 11.CD 12.AB
12.当BM与平面α平行时,cosθ=1;由最小角定理,直线与平面所成的角是直线与平面内的线所成角中
最小的角,所以θ小于等于BM与AC所成的角,分别取SC,SA的中点M,N,连接MN,BM,BN.
10 10 10
在△BMN 中,BM = BN = ,MN =1,得cos∠BMN = ,故cosθ∈ ,1.
2 10 10
6− 2 1
因为cos75°=cos ( 45°+30°)= ,cos60°= ,
4 2
6− 2 10 1
而 < < ,所以0°≤θ<75°.
4 10 2
故选:AB.
三、填空题:本题共 4小题,每小题 5分,共 20分.
32 4
13.2 14.6 15. π 16.
9 3
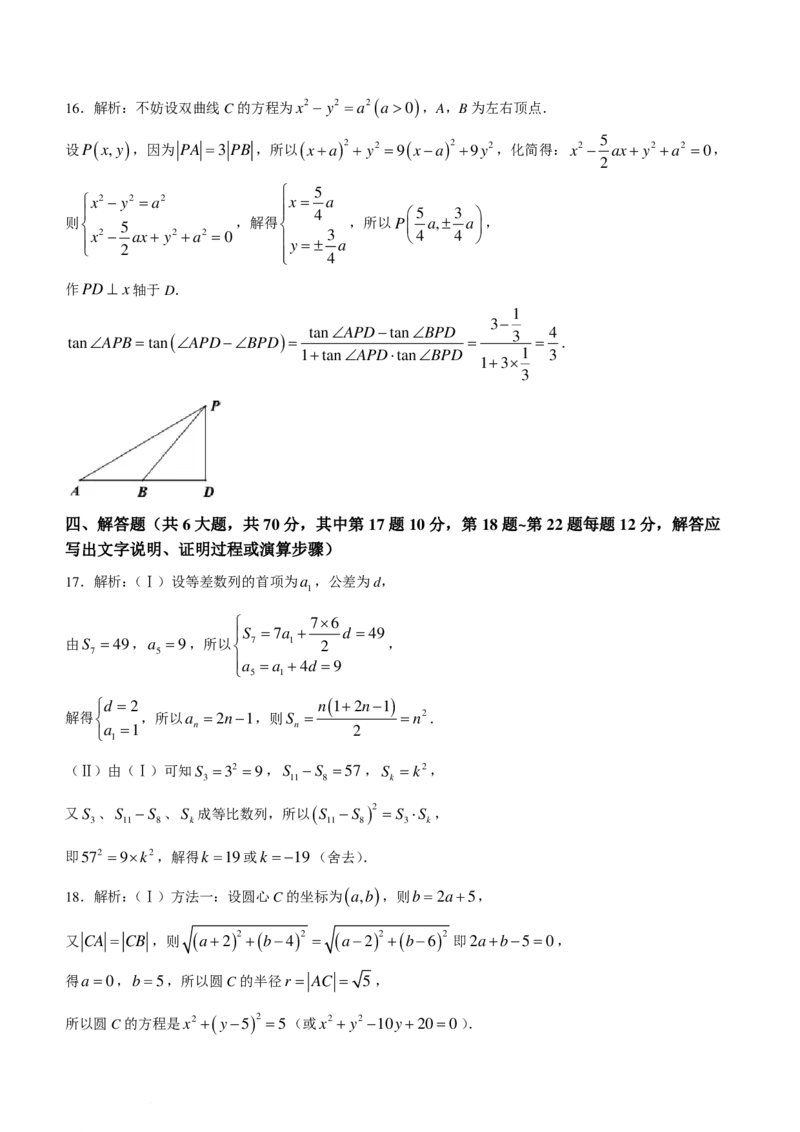
学科网(北京)股份有限公司16.解析:不妨设双曲线C的方程为x2 − y2 =a2( a>0 ),A,B为左右顶点.
5
设P ( x,y ),因为 PA =3 PB ,所以( x+a )2 + y2 =9 ( x−a )2 +9y2,化简得:x2 − ax+ y2 +a2 =0,
2
5
x2 − y2 =a2 x= a
4 5 3
则 5 ,解得 ,所以P a,± a ,
x2 − ax+ y2 +a2 =0 3 4 4
2 y =± a
4
作PD⊥ x轴于D.
1
3−
tan∠APB=tan (∠APD−∠BPD )= tan∠APD−tan∠BPD = 3 = 4 .
1+tan∠APD⋅tan∠BPD 1 3
1+3×
3
四、解答题(共 6大题,共 70分,其中第 17题 10分,第 18题~第22题每题 12分,解答应
写出文字说明、证明过程或演算步骤)
17.解析:(Ⅰ)设等差数列的首项为a ,公差为d,
1
7×6
S =7a + d =49
由S =49,a =9,所以 7 1 2 ,
7 5
a =a +4d =9
5 1
d =2 n ( 1+2n−1 )
解得 ,所以a =2n−1,则S = =n2.
a =1 n n 2
1
(Ⅱ)由(Ⅰ)可知S =32 =9,S −S =57,S =k2,
3 11 8 k
又S 、S −S 、S 成等比数列,所以( S −S )2 =S ⋅S ,
3 11 8 k 11 8 3 k
即572 =9×k2,解得k =19或k =−19(舍去).
18.解析:(Ⅰ)方法一:设圆心C的坐标为(
a,b
),则b=2a+5,
又 CA = CB ,则 ( a+2 )2 +( b−4 )2 = ( a−2 )2 +( b−6 )2 即2a+b−5=0,
得a=0,b=5,所以圆C的半径r = AC = 5 ,
所以圆C的方程是x2 +( y−5 )2 =5(或x2 + y2 −10y+20=0).
学科网(北京)股份有限公司1
方法二:AB的中点坐标为( 0,5 ),k = ,则AB的中垂线方程为y =−2x+5.
AB 2
y =2x+5 x=0
则 ,解得 ,所以圆心C的坐标为( 0,5 ),
y =−2x+5 y =5
所以圆C的半径r = AC = 5,
所以圆C的方程是x2 +( y−5 )2 =5(或x2 + y2 −10y+20=0).
(Ⅱ)设圆心C到直线的距离为d,
5 ( 3m−1 )−( 5+5m ) 10m−10
由题意可得d = = = 5,
( 1+m )2 +( 3m−1 )2 10m2 −4m+2
3
平方整理后可得5m2 −18m+9=0,解得m= 或m=3.
5
19.解析:(Ⅰ)取BC的中点M,连接AM,AB,AC,AM ,
1 1 1
∵三棱柱ABC−ABC 中,AB= BC =CA,∴AM ⊥ BC,
1 1 1
又∵∠AAB=∠AAC,∴△AAB≌△AAC,∴AB= AC,∴AM ⊥ BC,
1 1 1 1 1 1 1
又AM AM =M ,∴BC ⊥面AAM ,∴BC ⊥ AA .
1 1 1
(Ⅱ)方法一:连接MN,在△AMN 中,AN = 13,AM = 3,MN =2,
AM2 +MN2 −AN2 3
即cos∠AMN = =− ,即∠AMN =150°.
2AM ⋅MN 2
如图建系,A ( 3,0,0 ) ,B ( 0,1,0 ),N ( − 3,0,1 ) ,
( ) ( )
有BA= 3,−1,0 ,AN = −2 3,0,1 ,
3x− y =0
设面ABN的法向量为n=( x,y,z ),则 ,
−2 3x+z =0
( )
解得面ABN的一个法向量n= 1, 3,2 3 ,
n⋅m
3
面AAN 的一个法向量m=( 0,1,0 ),∴ cos n,m = = ,
1 n m 4
3
所以平面AAN与平面ANB的夹角的余弦值为 .
1 4
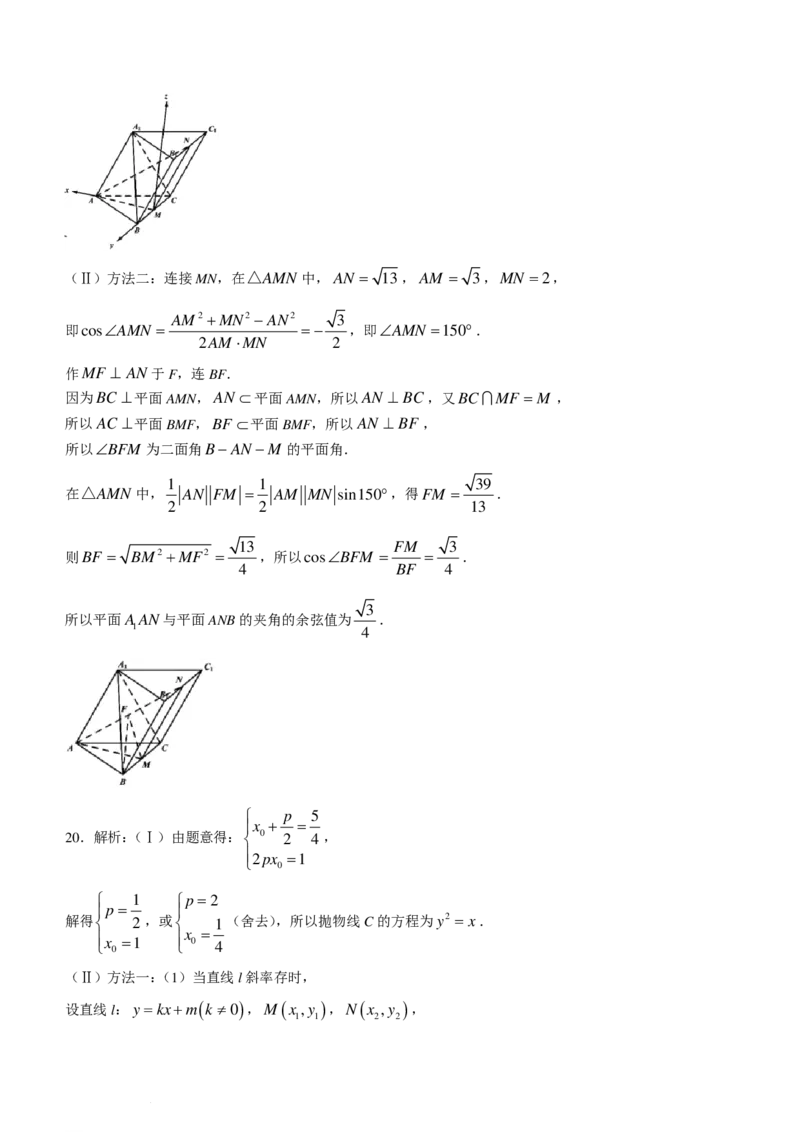
学科网(北京)股份有限公司(Ⅱ)方法二:连接MN,在△AMN 中,AN = 13,AM = 3,MN =2,
AM2 +MN2 −AN2 3
即cos∠AMN = =− ,即∠AMN =150°.
2AM ⋅MN 2
作MF ⊥ AN于F,连BF.
因为BC ⊥平面AMN,AN ⊂平面AMN,所以AN ⊥ BC,又BCMF =M ,
所以AC ⊥平面BMF,BF ⊂平面BMF,所以AN ⊥ BF ,
所以∠BFM 为二面角B−AN −M 的平面角.
1 1 39
在△AMN 中, AN FM = AM MN sin150°,得FM = .
2 2 13
13 FM 3
则BF = BM2 +MF2 = ,所以cos∠BFM = = .
4 BF 4
3
所以平面AAN与平面ANB的夹角的余弦值为 .
1 4
p 5
x + =
20.解析:(Ⅰ)由题意得: 0 2 4,
2px =1
0
1 p=2
p =
解得 2 ,或 1 (舍去),所以抛物线C的方程为y2 = x.
x =1 x 0 = 4
0
(Ⅱ)方法一:(1)当直线l斜率存时,
设直线l:y =kx+m ( k ≠0 ),M ( x ,y ),N ( x ,y ),
1 1 2 2
学科网(北京)股份有限公司y2 = x
则 ,消去x,整理得ky2 − y+m=0,
y =kx+m
1 m
则∆=1−4km>0,y + y = ,y ⋅y = ,
1 2 k 1 2 k
y −1 y −1 1 1 k 1
而k ⋅k = 1 ⋅ 2 = = = =− ,
1 2 x −1 x −1 ( y +1 )( y +1 ) y y +( y + y )+1 m+k+1 2
1 2 1 2 1 2 1 2
整理得m+3k+1=0,所以m=−1−3k,
所以直线l:y =kx−1−3k =k ( x−3 )−1,所以直线l过定点( 3,−1 ).
(2)当直线l斜率不存时,设直线l:x=m ( m>0,m≠1 ),
( ) ( ) m −1 − m −1 −1 1
则M m, m ,N m,− m ,则k ⋅k = ⋅ = =− ,得m=3,
1 2 m−1 m−1 m−1 2
所以直线l:x=3,则点( 3,−1 )在直线l上.
综上:直线l过定点( 3,−1 ).
( ) ( )
(Ⅱ)方法二:设M t2,t ,N t 2,t ,
1 1 2 2
t −1 t −1 1 1
则k ⋅k = 1 ⋅ 2 = =− ,
1 2 t2 −1 t 2 −1 ( t +1 )( t +1 ) 2
1 2 1 2
则tt =−3−( t +t ),直线l的方程为y−t = t 2 −t 1 ( x−t2 ) ,
1 2 1 2 1 t 2 −t2 1
2 1
1 tt 1 −3−( t +t ) 1
则y = x+ 1 2 = x+ 1 2 = ( x−3 )−1,
t +t t +t t +t t +t t +t
2 1 1 2 2 1 1 2 2 1
所以直线l过定点( 3,−1 ).
a −1
21.解析:(1)当 p =0时,则 n+1 =1,得a −1=a ,所以a −a =1,
a n+1 n n+1 n
n
所以数列{ a }是以a =2为首项,公差为1的等差数列.
n 1
所以a =2+( n−1 )×1=n+1,则3n⋅a =( n+1 )⋅3n,
n n
所以S =2×3+3×32 +4×33++( n+1 )⋅3n,
n
3S =2×32 +3×33+4×34 ++( n+1 )⋅3n+1,
n
学科网(北京)股份有限公司两式相减得−2S =6+32 +33+34 ++3n −( n+1 )⋅3n+1
n
32× ( 1−3n−1 )
3 2n+1
=6+ −( n+1 )⋅3n+1,所以S =− + ⋅3n+1.
1−3 n 4 4
a −1
(Ⅱ)当 p=1时,由 n+1 =a −1,得a =a2 −a +1,
a n n+1 n n
n
所以a −a =a2 −2a +1=( a −1 )2 >0,
n+1 n n n n
所以数列{ a }单调递增,因为a =2,所以a ≥2,
n 1 n
a −1
又由 n+1 =a −1,可得a −1=a ( a −1 ),
a n n+1 n n
n
1 1 1 1 1 1 1
所以 = = − ,即 = − ,
a −1 a ( a −1 ) a −1 a a a −1 a −1
n+1 n n n n n n n+1
1 1 1 1 1 1 1 1 1 1 1
则T = + ++ = − + − ++ − = − ,
n a a a a −1 a −1 a −1 a −1 a −1 a −1 a −1 a −1
1 2 n 1 2 2 3 n n+1 1 n+1
1 1
所以T =1− ,易知1− 为递增数列,且a =3,
n a −1 a −1 2
n+1 n+1
1 1 1 1
所以 =1− ≤1− <1,即: ≤T <1.
2 a −1 a −1 2 n
2 n+1
c 7
=
a 2
22.解析:(Ⅰ)由题意得:c2 =a2 +b2 ,解得b= 3,
a =2
x2 y2
所以双曲线C 的方程为 − =1.
1 4 3
y
(Ⅱ)方法一:设直线AP:y = 0 ( x+2 ),D ( x ,y ),
x +2 1 1
0
y
y = 0 ( x+2 ) 4y2 16y2 16y2
则 x +2 ,消y得:3+ 0 x2 + 0 x+ 0 −12=0,
3x2 + 0 4y2 =12 ( x 0 +2 )2 ( x 0 +2 )2 ( x 0 +2 )2
学科网(北京)股份有限公司16y2 −12 ( x +2 )2
得:−2x = 0 0 ,
1 3 ( x +2 )2 +4y2
0 0
x2 y2
又因为P ( x ,y )在双曲线上,满足 0 − 0 =1,即4y2 =3x2 −12,
0 0 4 3 0 0
8y2 −6 ( x +2 )2 6x2 −24−6 ( x +2 )2 −24 ( x +2 ) −4 4
所以−x = 0 0 = 0 0 = 0 = ,即x = .
1 3 ( x +2 )2 +4y2 3 ( x +2 )2 +3x2 −12 6x ( x +2 ) x 1 x
0 0 0 0 0 0 0 0
y 4 4
同理设直线BP:y = 0 ( x−2 ),E ( x ,y ),可得x = ,所以x = .
x −2 2 2 2 x Q x
0 0 0
4 2
因为x =λ2x ,所以 =λ2x ,因为x >0,所以x = .
Q 0 x 0 0 0 λ
0
4
2 λ2 y 2 3−3λ2 2 3−3λ2
把x = 代入双曲线方程得 − 0 =1,解得 y = ,则点P , .
0 λ 4 3 0 λ λ λ
设△DBP与△ABD的外接圆的半径分别为r ,r ,
1 2
PB AB
由正弦定理得2r = ,2r = ,
1 sin∠BDP 2 sin∠ADB
因为∠ADB+∠BDP=180°,所以sin∠BDP=sin∠ADB.
2 2
2 3 1 4 9
−2 + −3 7 − −
S r BP λ λ2 λ 7 7
则 1 = 1 = = = .
S r AB 4 4
2 2
1 1 S 13
因为0<λ< ,所以 >2,所以 1 ∈ ,+∞.
2 λ S 4
2
(Ⅱ)方法二:设直线DE:x=ty+m,D ( x ,y ),E ( x ,y ),
1 1 2 2
x=ty+m
( )
则 ,消x得: 3t2 +4 y2 +6tmy+3m2 −12=0,
3x2 +4y2 =12
−6tm 3m2 −12 4−m2
所以y + y = ,y y = ,得y y = ( y + y ),
1 2 3t2 +4 1 2 3t2 +4 1 2 2mt 1 2
y y
因为P,A,D三点共线,则 1 = 0 ,
x +2 x +2
1 0
学科网(北京)股份有限公司y y y ( x −2 ) x −2
因为P,B,E三点共线,则 2 = 0 ,两式相除得 1 2 = 0 ,
x −2 x −2 y ( x +2 ) x +2
2 0 2 1 0
y ( x −2 ) y ( ty +m−2 ) ty y +( m−2 ) y ( 4−m2 )( y + y )+2m ( m−2 ) y
而 1 2 = 1 2 = 1 2 1 = 1 2 1
y ( x +2 ) y ( ty +m+2 ) ty y +( m+2 ) y ( 4−m2 )( y + y )+2m ( m+2 ) y
2 1 2 1 1 2 2 1 2 2
( 2−m ) ( 2+m ) y +( 2−m ) y 2−m
= 1 2 = .
( 2+m )( 2+m ) y +( 2−m ) y 2+m
1 2
因为x =λ2x ,所以m=λ2x .
Q 0 0
2−m x −2 2−λ2x x −2 2
因为 = 0 ,所以 0 = 0 ,得x = ,
2+m x +2 2+λ2x x +2 0 λ
0 0 0
4
2 λ2 y 2 3−3λ2 2 3−3λ2
把x = 代入双曲线方程得 − 0 =1,解得y = ,则点P , .
0 λ 4 3 0 λ λ λ
设△DBP与△ABD的外接圆的半径分别为r ,r ,
1 2
PB AB
由正弦定理得2r = ,2r = ,
1 sin∠BDP 2 sin∠ADB
因为∠ADB+∠BDP=180°,所以sin∠BDP=sin∠ADB,
2 2
2 3 1 4 9
−2 + −3 7 − −
S r BP λ λ2 λ 7 7
则 1 = 1 = = = ,
S r AB 4 4
2 2
1 1 S 13
因为0<λ< ,所以 >2,所以 1 ∈ ,+∞.
2 λ S 4
2
学科网(北京)股份有限公司