江西省八所重点中学2024届高三下学期4月联考数学试卷(无答案)_2024年4月_01按日期_3号_2024届江西省八所重点中学高三下学期4月联考_2024届江西省八所重点中学高三下学期4月联考数学

江西省八所重点中学 2024 届高三联考 数学试卷 2024.4 命题：吉安一中 罗爱军 李云 新余一中艾青梅 （考试时间：120分钟，试卷满分：150分） 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上． 2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑．如需改动， 用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上．写在本试 卷上无效， 3．考试结束后，将本试卷和答题卡一并交回． 一、单选题：本大题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有一 项是符合题目要求的． 1．抛物线的焦点坐标为（ ）  1  1  1 A．0,1 B．  0,  C．  0,  D．  0,   2  4  8  π 2π   π π  2．已知集合 Ax 2kπ  x2kπ ,kZ，集合 Bx kπ  xkπ ,kZ，则  6 3   4 3  AI B（ ）  π π  π π A．  2kπ ,2kπ  ，kZ B．  kπ ,kπ  ，kZ  4 3  4 3  π π  π π C．  2kπ ,2kπ  ，kZ D．  kπ ,kπ  ，kZ  6 3  6 3 3．已知S 是正项等比数列a 的前n项和，a a 82，a a 81，则S （ ） n n 1 5 2 4 5 A．212 B．168 C．121 D．163  3 1 uuur 4．复数Z在复平面内对应的点为Z , ，O为坐标原点，将向量OZ 绕点O逆时针旋转90°后得到向   2 2   uuuur 量OZ ，点Z 对应复数为Z ，则Z5 （ ） 1 1 1 1 1 3 1 3 1 3 A．  i B．1i C．  i D．  i 2 2 2 2 4 4 5．函数 f x 2xm  lnx 有且只有一个零点，则m的取值可以是（ ） A．2 B．1 C．3 D．e 6．已知正四棱锥PABCD，现有五种颜色可供选择，要求给每个顶点涂色，每个顶点只涂一种颜色，且 学科网（北京）股份有限公司同一条棱上的两个顶点不同色，则不同的涂色方法有（ ） A．240 B．420 C．336 D．120 7．已知，   0, π  ，2  sinsin2   sin2 ，则tan   2 π  （ ）  2 tan  6 3 3 A． 3 B． C． D． 3 3 3 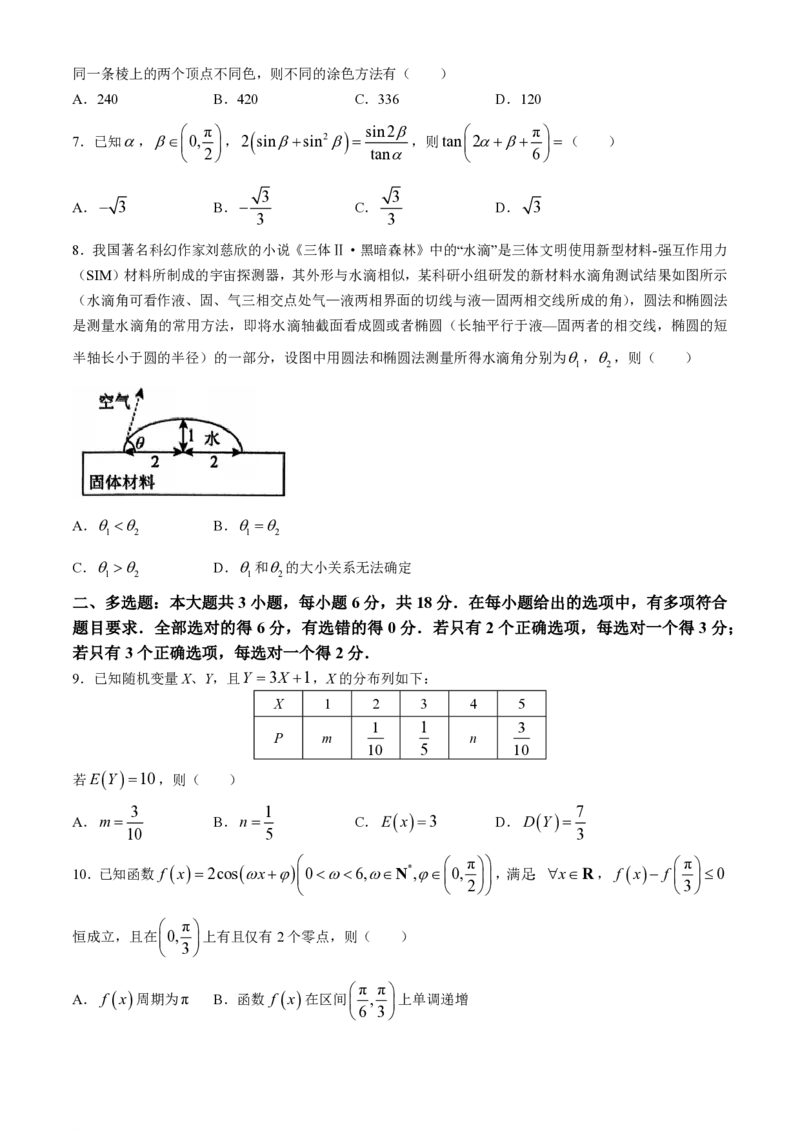8．我国著名科幻作家刘慈欣的小说《三体Ⅱ·黑暗森林》中的“水滴”是三体文明使用新型材料-强互作用力 （SIM）材料所制成的宇宙探测器，其外形与水滴相似，某科研小组研发的新材料水滴角测试结果如图所示 （水滴角可看作液、固、气三相交点处气—液两相界面的切线与液—固两相交线所成的角），圆法和椭圆法 是测量水滴角的常用方法，即将水滴轴截面看成圆或者椭圆（长轴平行于液—固两者的相交线，椭圆的短 半轴长小于圆的半径）的一部分，设图中用圆法和椭圆法测量所得水滴角分别为，，则（ ） 1 2 A．  B．  1 2 1 2 C．  D．和的大小关系无法确定 1 2 1 2 二、多选题：本大题共 3小题，每小题 6分，共 18分．在每小题给出的选项中，有多项符合 题目要求．全部选对的得 6 分，有选错的得 0 分．若只有 2 个正确选项，每选对一个得 3 分； 若只有 3个正确选项，每选对一个得 2分． 9．已知随机变量X、Y，且Y 3X 1，X的分布列如下： X 1 2 3 4 5 1 1 3 P m n 10 5 10 若EY10，则（ ） 3 1 7 A．m B．n C．Ex3 D．DY 10 5 3   π π 10．已知函数 f x2cosx  06,N*,  0,  ，满足：xR， f x f   0   2 3  π 恒成立，且在  0,  上有且仅有2个零点，则（ ）  3 π π A． f x周期为π B．函数 f x在区间  ,  上单调递增 6 3 学科网（北京）股份有限公司π  π kπ  C．函数 f x的一条对称轴为x D．函数 f x的对称中心为   ,0  kZ 3 30 5  11．在棱长为2的正方体ABCDABC D 中，点E，F分别为棱DD ，CD 的中点，过点E的平面与 1 1 1 1 1 1 1 平面BDC 平行，点G为线段BC 上的一点，则下列说法正确的是（ ） 1 1 A．AG  BD 1 1 B．若点Q为平面内任意一点，则QCQB的最小值为2 6 1 C．底面半径为 且高为 3的圆柱可以在该正方体ABCDABC D 内任意转动 2 1 1 1 1 2 2 D．直线AG与平面BDC 所成角的正弦值的最大值为 1 1 3 三、填空题：本题共 3小题，每小题 5分，共 16分．把答案填在答题卡中的横线上． 5  2  12．  x2  1  展开式中x2项系数为________．  x  BD 1 13．在三角形ABC中，BC 4，角A的平分线AD交BC于点D，若  ，则三角形ABC面积的最 DC 3 大值为________． 2x1 n1 14．已知函数 f x 1a ，存在实数x ,x ,,x 使得 f x  f x 成立，若正整数n的 2x 2x 1 2 n i n i1 最大值为8，则正实数a的取值范围是________． 四、解答题：本题共 5小题，共 77分，解答应写出文字说明、证明过程或演算步骤． 15．（13分）数列a 满足a  π ，a     π , π  ，tana  1 ，  nN* ． n 1 6 n  2 2 n1 cosa n （1）证明：数列  tan2a  为等差数列，并求数列tana 的通项公式； n n 1 （2）求正整数m，使得sina sina sina  ． 1 2 m 100 2π 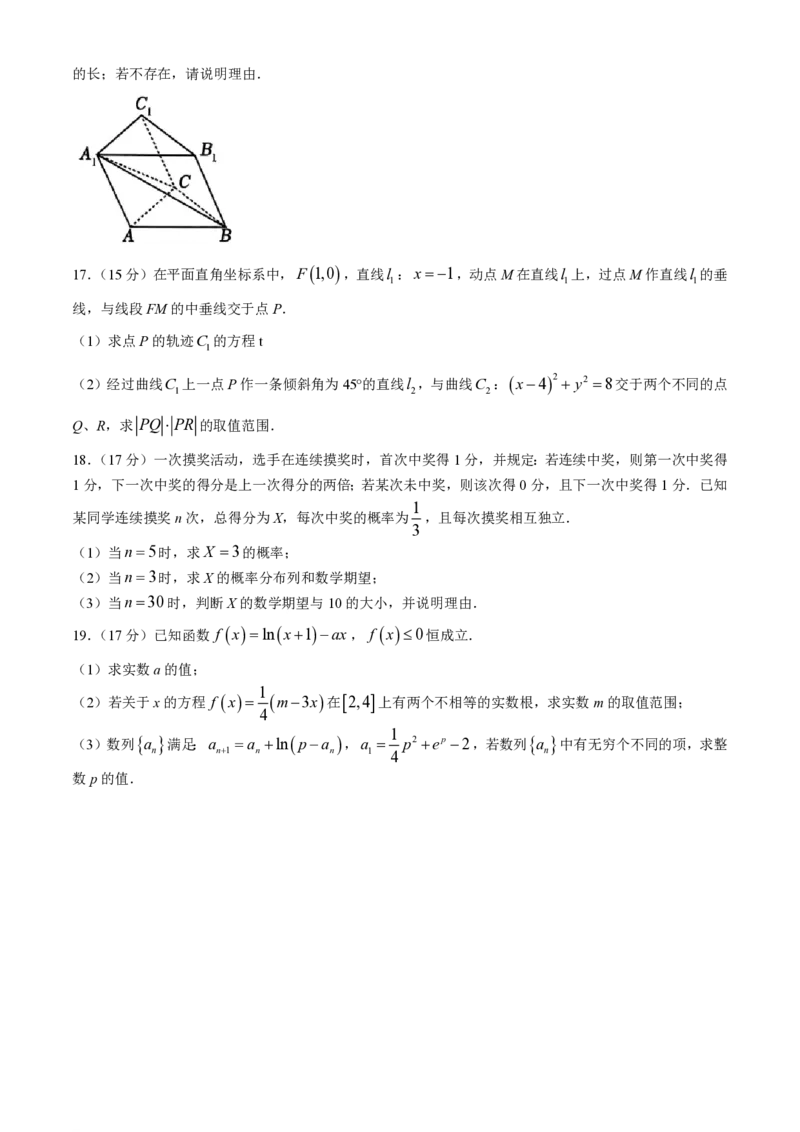16．（15分）三棱柱ABCABC 中，AB AC，AB AC 2，侧面AACC 为矩形，AAB ， 1 1 1 1 1 1 3 2 3 三棱锥C ABC 的体积为 ． 1 3 （1）求侧棱AA 的长； 1 5 （2）侧棱CC 上是否存在点E，使得直线AE与平面ABC所成角的正弦值为 ？若存在，求出线段CE 1 1 5 1 学科网（北京）股份有限公司的长；若不存在，请说明理由． 17．（15分）在平面直角坐标系中，F1,0，直线l ：x1，动点M在直线l 上，过点M作直线l 的垂 1 1 1 线，与线段FM的中垂线交于点P． （1）求点P的轨迹C 的方程t 1 （2）经过曲线C 上一点P作一条倾斜角为45°的直线l ，与曲线C ：x42  y2 8交于两个不同的点 1 2 2 Q、R，求 PQ  PR 的取值范围． 18．（17分）一次摸奖活动，选手在连续摸奖时，首次中奖得1分，并规定：若连续中奖，则第一次中奖得 1分，下一次中奖的得分是上一次得分的两倍；若某次未中奖，则该次得0分，且下一次中奖得1分．已知 1 某同学连续摸奖n次，总得分为X，每次中奖的概率为 ，且每次摸奖相互独立． 3 （1）当n5时，求X 3的概率； （2）当n3时，求X的概率分布列和数学期望； （3）当n30时，判断X的数学期望与10的大小，并说明理由． 19．（17分）已知函数 f xlnx1ax， f x0恒成立． （1）求实数a的值； 1 （2）若关于x的方程 f x m3x在2,4上有两个不相等的实数根，求实数m的取值范围； 4 1 （3）数列a 满足：a a lnpa ，a  p2 ep 2，若数列a 中有无穷个不同的项，求整 n n1 n n 1 4 n 数p的值． 学科网（北京）股份有限公司