文档内容
吉安一中 2024 届高三“九省联考”考后适应性测试数
学试题一
本套试卷根据九省联考题型命制,题型为8+3+3+5模式
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.(本题5分)某校高一年级15个班参加朗诵比赛的得分如下:
85 87 88 89 89 90 91 91 92 93 93 93 94 96 98
则这组数据的40%分位数为( )
A.90 B.91 C.90.5 D.92
2.(本题5分)已知圆C: 及点 ,则下列说法正确的是
( )
A.直线 与圆C始终有两个交点
B.若M是圆C上任一点,则|MQ|的取值范围为
C.若点 在圆C上,则直线PQ的斜率为
D.圆C与 轴相切
3.(本题5分)已知向量 满足 与 垂直,则 的最小
值为( )
A. B. C.1 D.3
4.(本题5分)高一(1)班有8名身高都不相同的同学去参加红歌合唱,他们站成
前后对齐的2排,每排4人,则前排的同学都比后排对应的同学矮的概率为( )
A. B. C. D.
5.(本题5分)已知数列 的前n项和分别为 ,记
,则数列 的前2021项和为( )
A. B. C. D.
试卷第1页,共3页
学科网(北京)股份有限公司6.(本题5分)已知球 的直径 , , , 是球 球面上的三点,
是等边三角形,且 ,则三棱锥 的体积为( ).
A. B. C. D.
7.(本题5分)已知 ,且 ,则 可能为( )
A. B. C. D.
8.(本题5分)已知f(x)为奇函数,当x∈[0,1]时, 当
,若关于x的不等式f(x+m)>f(x)恒成立,则实数m的取值范围
为( )
A.(-1,0)∪(0,+∞) B.
C. D. (2,+∞)
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项
符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.(本题6分)下列选项中的两个集合相等的有( ).
A.
B.
C.
D.
10.(本题6分)如图,一个质点在半径为2的圆 上以点 为起始点,沿逆时针方
向运动,每 转一圈.则该质点到 轴的距离 是关于运动时间 的函数,则下列说法
正确的是( )
试卷第2页,共3页A.函数 的最小正周期是
B.函数 的最小正周期是
C.
D.
11.(本题6分)定义:对于定义在区间I上的函数 和正数 ,若存在
正数M,使得不等式 对任意 恒成立,则称函数
在区间I上满足 阶李普希兹条件,则下列说法正确的有( )
A.函数 在 上满足 阶李普希兹条件
B.若函数 在 上满足一阶李普希兹条件,则M的最小值为
C.若函数 在 上满足 的一阶李普希兹条件,且方程
在区间 上有解 ,则 是方程 在区间 上的唯一解
D.若函数 在 上满足 的一阶李普希兹条件,且 ,则对任
意函数 , ,恒有
三、填空题:本题共3小题,每小题5分,共15分.
12.(本题5分)已知复数 ,则z在复平面内对应的点所在的
象限为 象限.
试卷第3页,共3页
学科网(北京)股份有限公司13.(本题5分)已知函数 ,若曲线 与曲线
存在公切线,则实数 的最大值为 .
14.(本题5分)地球仪是地理教学中的常用教具.如图1所示,地球仪的赤道面(与转
轴垂直)与黄道面(与水平面平行)存在一个夹角,即黄赤交角,大小约为23.5°.为锻炼动
手能力,某同学制作了一个半径为4cm的地球仪(不含支架),并将其放入竖直放置的
正三棱柱 中(姿态保持不变),使地球仪与该三棱柱的三个侧面相切,如图
2所示.此时平面 恰与地球仪的赤道面平行,则三棱柱 的外接球体积
为 .(参考数据: )
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)为落实中央“坚持五育并举,全面发展素质教育,强化体育锻炼”
的精神,某高中学校鼓励学生自发组织各项体育比赛活动,甲、乙两名同学利用课余时
间进行乒乓球比赛,规定:每一局比赛中获胜方记1分,失败方记0分,没有平局,
首先获得5分者获胜,比赛结束.假设每局比赛甲获胜的概率都是 .
(1)求比赛结束时恰好打了6局的概率;
(2)若甲以3:1的比分领先时,记X表示到结束比赛时还需要比赛的局数,求X的
分布列及期望.
16.(本题15分)已知函数 .
(1)若函数 在 处的切线与直线 垂直,求实数 的值.
试卷第4页,共3页(2)若函数 存在两个极值点,求实数 的取值范围.
17.(本题15分)如图,在正三棱锥 中,有一半径为1的半球,其底面圆O
与正三棱锥的底面贴合,正三棱锥的三个侧面都和半球相切.设点D为BC的中点,
.
(1)用 分别表示线段BC和PD长度;
(2)当 时,求三棱锥的侧面积S的最小值.
18.(本题17分)如图,D为圆O: 上一动点,过点D分别作x轴,y轴的
垂线,垂足分别为A,B,连接 并延长至点W,使得 ,点W的轨迹记为曲线
.
(1)求曲线C的方程;
(2)若过点 的两条直线 , 分别交曲线C于M,N两点,且 ,求证:直
线MN过定点;
(3)若曲线C交y轴正半轴于点S,直线 与曲线C交于不同的两点G,H,直线
SH,SG分别交x轴于P,Q两点.请探究:y轴上是否存在点R,使得
?若存在,求出点R坐标;若不存在,请说明理由.
19.(本题17分)对于无穷数列 ,“若存在 ,必有
试卷第5页,共3页
学科网(北京)股份有限公司”,则称数列 具有 性质.
(1)若数列 满足 ,判断数列 是否具有 性质?
是否具有 性质?
(2)对于无穷数列 ,设 ,求证:若数列 具有 性质,
则 必为有限集;
(3)已知 是各项均为正整数的数列,且 既具有 性质,又具有 性质,
是否存在正整数 , ,使得 , , ,…, ,…成等差数列.若存在,请
加以证明;若不存在,说明理由.
试卷第6页,共3页参考答案:
1.C
【详解】由题意, ,故这组数据的40%分位数为从小到大第6,7位数据的平均
数,即 .
故选:C
2.B
【详解】依题意,圆C: ,圆心 ,半径 ,
对于A,直线 恒过定点 ,而点 在圆C外,则过点 的直线与
圆C可能相离,A不正确;
对于B, ,点Q在圆C外,由 得: ,
B正确.
对于C,点 在圆C上,则 ,解得 ,而点 ,
则直线PQ的斜率为 ,C不正确;
对于D,点 到x轴距离为7,大于圆C的半径,则圆C与 轴相离,即圆C与x轴不
相切,D不正确;
故选:B
3.C
【详解】由 与 垂直,得 ,则 ,
所以 1,
所以当 时, 的最小值为
故选:C
4.D
【详解】 名身高都不相同的同学站在8个不同的位置有 种站法,将8名同学分为4组,
答案第1页,共2页
学科网(北京)股份有限公司每组2人,则有 种分法,4组人有 种站法,故所求概率
.
故选:D.
5.C
【详解】当 时, ,
当 时,
,
所以
.
故选:C
6.A
【详解】设球心为 ,等边三角形 截面小圆的圆心为 (也是等边三角形 的中
心).
由于 是等边三角形, ,
所以 平面 , 在面 的投影即 ,也即等边三角形 的中心,且 平
面 ,则 .
因为 是直径,所以 .
所以 , .
由于 是等边三角形 的中心,所以 ,
答案第2页,共2页所以等边三角形 的高 , .
所以三棱锥 的体积为 .
故选:A
7.B
【详解】由 ,得 ,
所以 ,
所以 ,
整理得 ,
,
所以 或 ,
所以 或 ,
①当 时, , ,
因为 ,所以 ,
答案第3页,共2页
学科网(北京)股份有限公司所以 ,
因为 ,所以 ,
②当 时, ,
因为 ,所以 ,
由于 ,所以解得 ,
③当 时, ,
因为 ,所以 ,
由于 ,所以解得 ,
综上, ,或 ,或 ,
故选:B
8.B
【详解】若 , ,则 , ,
则 ,
是奇函数,
,
则 , , ,
若 , ,则 , ,
答案第4页,共2页则 ,
则 , , ,
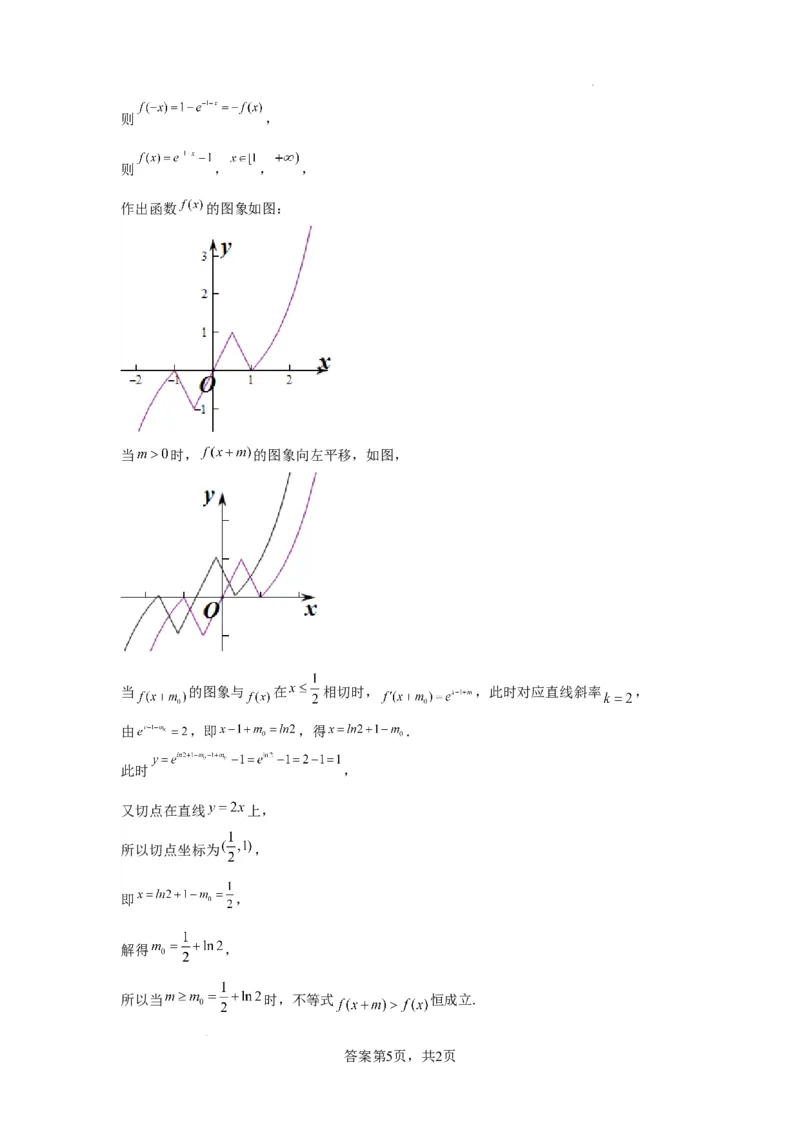
作出函数 的图象如图:
当 时, 的图象向左平移,如图,
当 的图象与 在 相切时, ,此时对应直线斜率 ,
由 ,即 ,得 .
此时 ,
又切点在直线 上,
所以切点坐标为 ,
即 ,
解得 ,
所以当 时,不等式 恒成立.
答案第5页,共2页
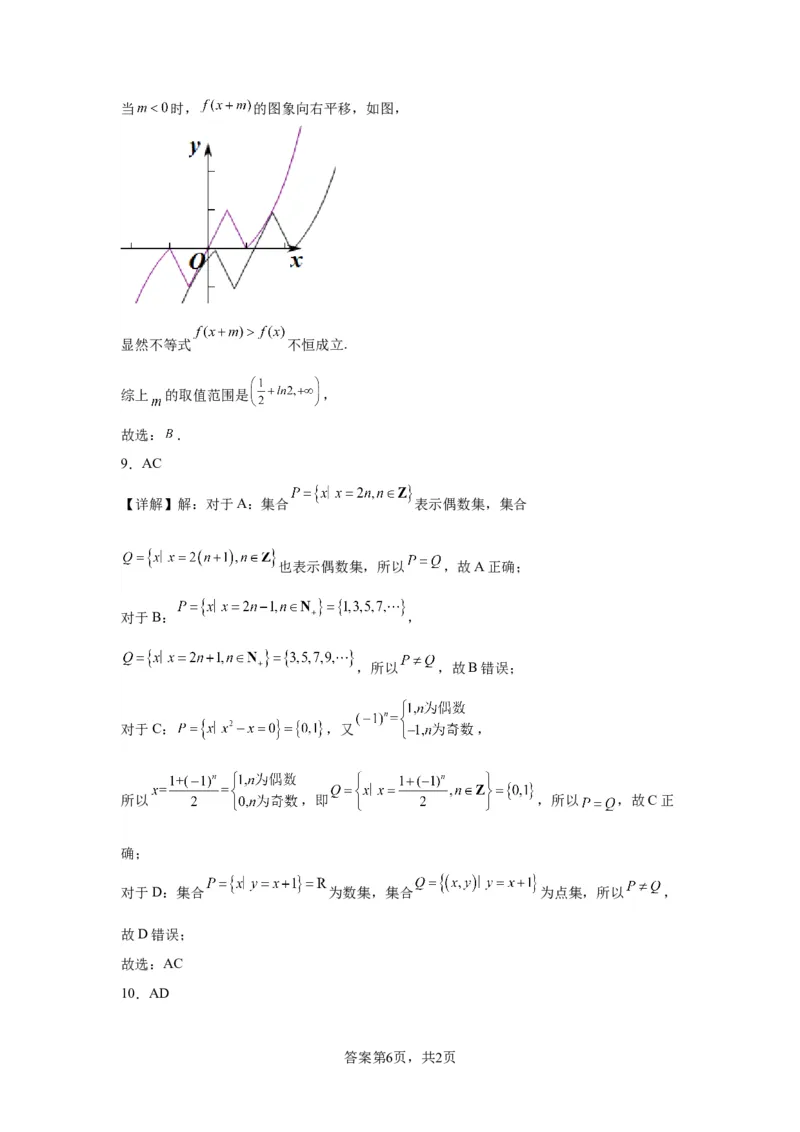
学科网(北京)股份有限公司当 时, 的图象向右平移,如图,
显然不等式 不恒成立.
综上 的取值范围是 ,
故选: .
9.AC
【详解】解:对于A:集合 表示偶数集,集合
也表示偶数集,所以 ,故A正确;
对于B: ,
,所以 ,故B错误;
对于C: ,又 ,
所以 ,即 ,所以 ,故C正
确;
对于D:集合 为数集,集合 为点集,所以 ,
故D错误;
故选:AC
10.AD
答案第6页,共2页【详解】由题可知,该质点的角速度为 ,
由于起始位置为点 ,沿逆时针方向运动,
设经过时间 s之后所成的角为 ,则 ,
根据三角函数定义可知点 的纵坐标为 ,
所以该质点到 轴的距离 ,可得D正确,C错误;
由解析式 可知其最小正周期为 ,即A正确,B错误;
故选:AD
11.ACD
【详解】A选项:不妨设 , ,即
,故 ,对 ,均有
,A选项正确;
B选项:不妨设 , 在 单调递增, ,
,即 ,即
对 , 恒成立,即 在 上单调递减, 对
恒成立,所以 对 恒成立,即 ,即 的最小值为 ,B
选项错误;
C选项:假设方程 在区间 上有两个解 , ,则
答案第7页,共2页
学科网(北京)股份有限公司,这与 矛盾,故只有唯一解,C选项正
确;
D选项:不妨设 ,当 时, ,当 时,
,故对 , ,故D选项正确;
故选:ACD
12.第二
【详解】由 ,可知 , ,
故z在复平面内对应的点所在的象限为第二象限.
故答案为:第二.
13.
【详解】 ,
假设两曲线在同一点 处相切,
则 ,可得 ,即 ,
因为函数 单调递增,且 时 ,
所以 ,则 ,此时两曲线在 处相切,
根据曲线的变化趋势,若 ,则两曲线相交于两点,不存在公切线,如图,
答案第8页,共2页所以 的最大值为 .
故答案为: .
14.
【详解】由题设可知平面 与面 的夹角为 ,取 中点M, 中点N,连
接MN
由二面角的定义可知 为平面 与面 的夹角,即
设正三棱柱的底面边长为 ,高为h,则
所以 ,则
又地球仪与该三棱柱的三个侧面相切,即地球仪的最大圆与底面正三角形内切,
所以内切圆的半径 ,解得
所以三棱柱的高 ,底面边长为
设三棱柱 上、下底面中心 ,连线的中点O为球心,
在直角 , ,
所以三棱柱外接球的半径
所以体积
故答案为:
答案第9页,共2页
学科网(北京)股份有限公司15.(1) ;(2)分布列答案见解析,数学期望: .
【详解】解:(1)比赛结束时恰好打了6局,甲获胜的概率为
,
恰好打了6局,乙获胜的概率为 ,
所以比赛结束时恰好打了6局的概率为 .
(2)X的可能取值为2,3,4,5,
,
,
,
.
所以X的分布列如下:
2 3 4 5
答案第10页,共2页故 .
16.(1) ;(2) .
【详解】(1) ,
,
则 ,解得 .
(2) ,
由题设可知 有两个不同的零点,且 在零点的附近 的符号发生变化.
令 ,则 ,
若 ,则 ,则 为 上为增函数,
在 上至多有一个零点.
当 时,若 ,则 ,故 在 上为增函数,
若 ,则 ,故 在 上为减函数,
故 ,故 .
又 且 ,故 在 上存在一个零点;
下证当 时,总有 .
令 ,则 ,
当 时, ,故 为 上的减函数,
答案第11页,共2页
学科网(北京)股份有限公司故 ,故 成立.
令 ,则 ,
故当 时,有 ,
取 ,则当 时,
有 ,
故 ,故在 上,存在实数 ,使得 ,
由零点存在定理及 的单调性可知可得 在 上存在一个零点.
综上可知,实数 的取值范围是 .
17.(1) ;
(2)
【详解】(1)连接OP,由题意O为 的中心,
且 面ABC,又 面ABC,所以 ,所以 为直角三角形.
设半球与面PBC的切点为E,则 且 .
答案第12页,共2页在 中, ,所以 .
在 中, .
(2)由题知, ,
化简得 , ,
令 ,则上述函数变形为 , ,
所以 ,令 ,得 .当 时,
, 单调递减,当 时,
, 单调递增,所以当 时,
三棱锥的侧面积S的最小值为 .
18.(1)
(2)证明见解析,
(3)存在,
【详解】(1)设 , ,则 ,
答案第13页,共2页
学科网(北京)股份有限公司由题意知 ,所以 ,得( ,所以 ,
因为 ,得 ,故曲线C的方程为 .
(2)由题意可知,直线 不平行坐标轴,
则可设 的方程为: ,此时直线 的方程为 .
由 ,消去 得: ,
解得: 或 (舍去),所以 ,
所以 ,同理可得: .
当 时,直线 的斜率存在,
,
则直线 的方程为 ,
所以直线 过定点 .
当 时,直线 斜率不存在,此时直线 方程为: ,也过定点 ,
综上所述:直线 过定点 .
(3)假设存在点R使得 ,设 ,
因为 ,所以 ,即 ,
答案第14页,共2页所以 ,所以 ,
直线 与曲线C交于不同的两点G、H,易知G、H关于 轴对称,
设 ,
易知点 ,直线 方程是 ,
令 得点P横坐标 ,
直线 方程是 ,令 得点Q横坐标 ,
由 ,得 ,又 在椭圆上,
所以 ,所以 ,解得 ,
所以存在点 ,使得 成立.
19.(1)见解析;
(2)见解析;
(3)见解析.
可证得存在整数 ,使得 是等差数列.
【详解】(1)因为 ,
,但 ,所以数列 不具有性质 ,
答案第15页,共2页
学科网(北京)股份有限公司同理可得数列 具有性质 ;
(2)因为数列 具有性质 ,
所以一定存在一组最小的且 ,满足 ,即 ,
由性质 的含义可得 , , , ,
所以数列 中,从第 项开始的各项呈现周期性规律:
为一个周期中的各项,
所以数列 中最多有 个不同的项,
所以 最多有 个元素,即 为有限集;
(3)因为数列 具有 性质,又具有 性质,
所以存在 ,使得 ,
其中 分别是满足上述关系式的最小的正整数,
由性质 的含义可得 ,
若 ,则取 ,可得 ,
若 ,则取 ,可得 ,
记 ,则对于 ,
有 ,显然 ,
由性质 的含义可得: ,
所以
,
答案第16页,共2页所以 ,
又 满足 的最小的正整数,
所以 , ,
所以 ,
所以 ,
取 ,所以,若 是偶数,则 ,
若 是奇数,
则 ,
所以, ,
所以 是公差为1的等差数列.
答案第17页,共2页
学科网(北京)股份有限公司