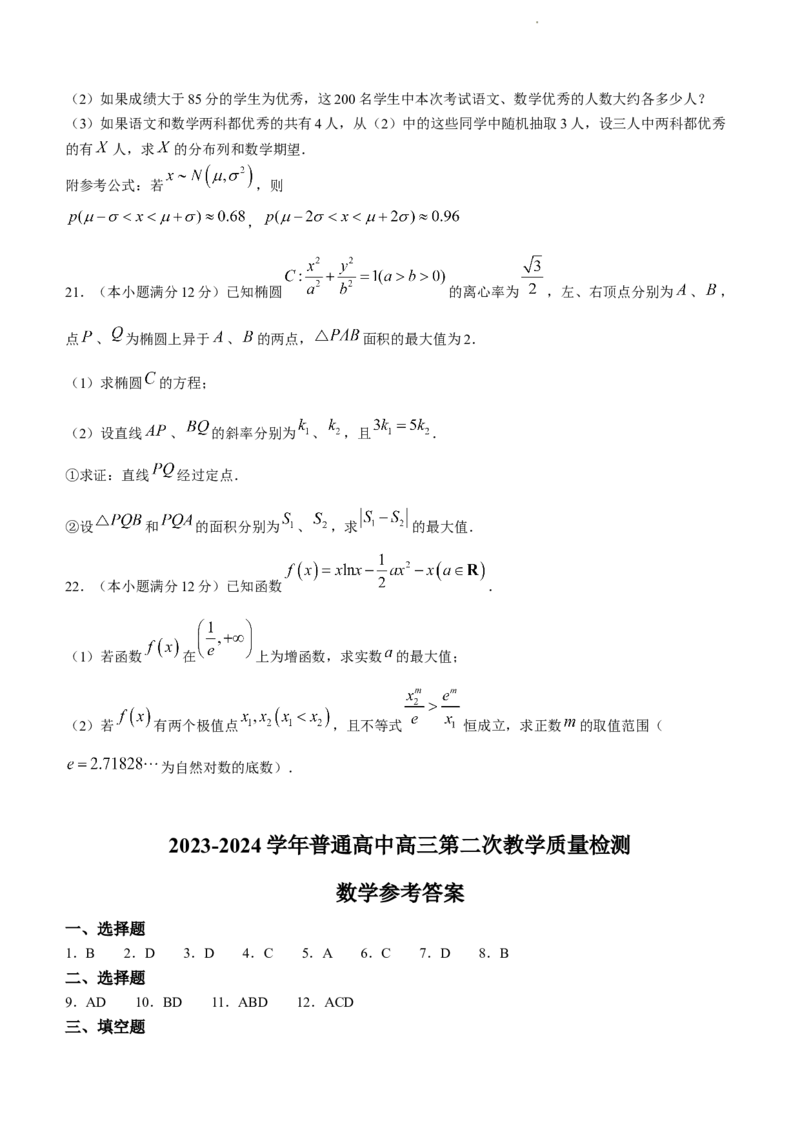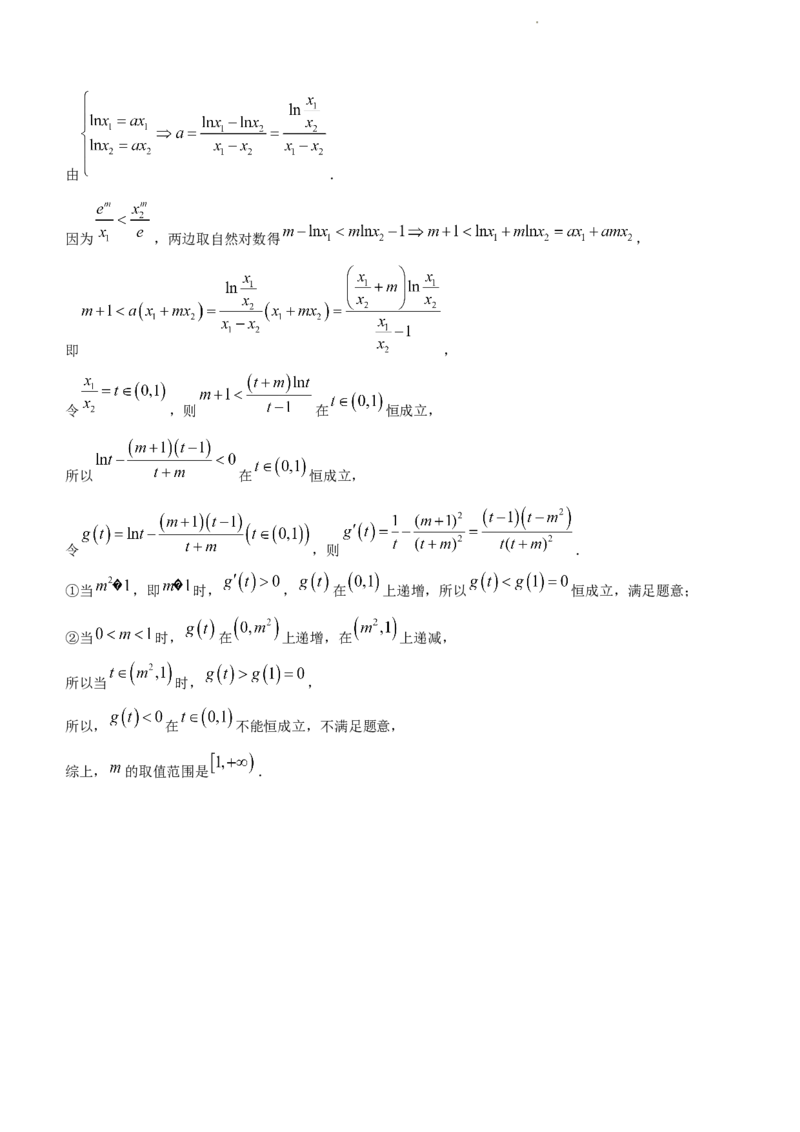文档内容
2023-2024 学年普通高中高三第二次教学质量检测
数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。考生作答时,将答案答在答题卡上,
在本试卷上答题无效。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,考生务必将本人的姓名、准考证号等考生信息填写在答题卡上,并用2B铅笔将准
考证号填涂在相应位置。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择
题答案使用0.5毫米的黑色墨水签字笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知集合 , ,则 等于
A. B. C. D.
2.若 ,则复数 在复平面内对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.设公差不为零的等差数列 的前 项和为 , ,则 等于
A.15 B.1 C. D.
4.已知向量 , 的夹角为 且 , ,则 在 上投影向量的坐标为
A. B. C. D.
5.“ ”是“ ”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
学科网(北京)股份有限公司6.过直线 上的一点 作圆 的两条切线 , ,切点分别为 , ,当直线 ,
关于 对称时,线段 的长为
A.4 B. C. D.2
7.已知抛物线 的焦点为 ,点 是 上一点,且 ,以 为直径的圆截 轴
所得的弦长为1,则 等于
A.2 B.2或4 C.4 D.4或6
8.随着城市经济的发展,早高峰问题越发严重,上班族需要选择合理的出行方式.某公司员工小明的上班出
行方式有三种,某天早上他选择自驾,坐公交车,骑共享单车的概率分别为 , , ,而他自驾,坐公交
车,骑共享单车迟到的概率分别为 , , ,结果这一天他迟到了,在此条件下,他自驾去上班的概率是
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
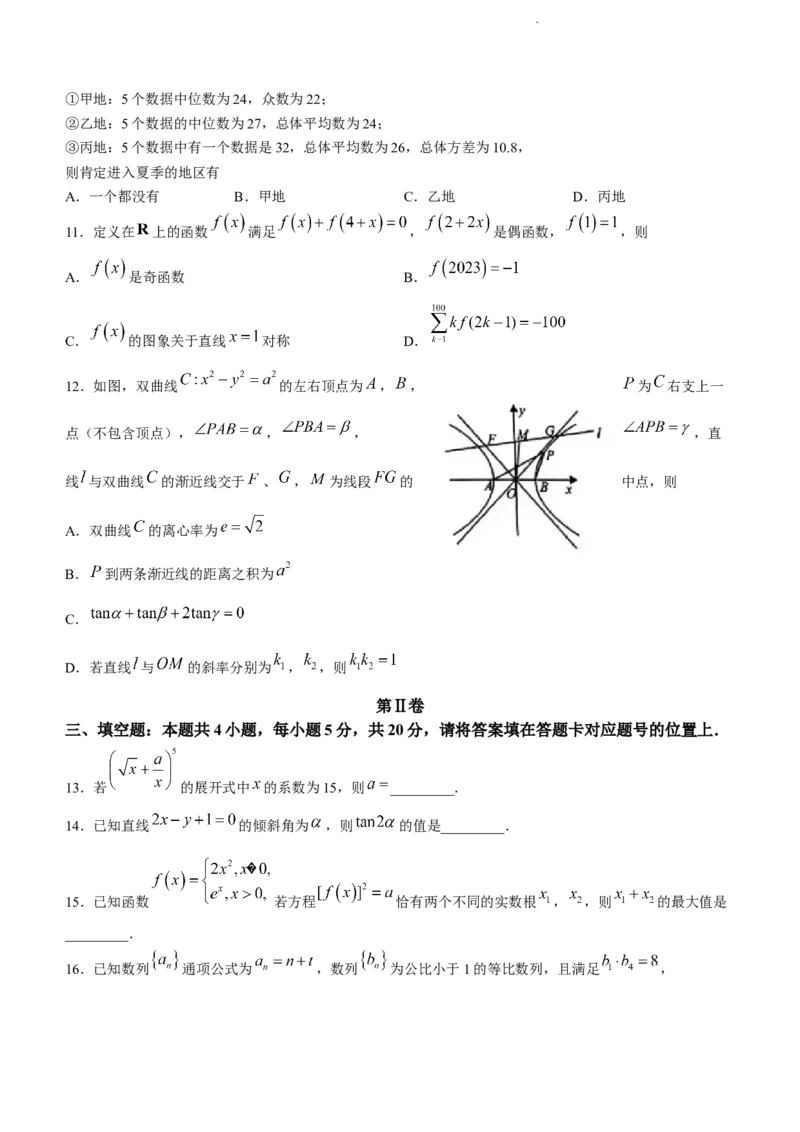
9.已知函数 的图象如图所示, , 是直线 与曲线 的两个交点,
且 ,则下列选项正确的是
A. 的值为3 B. 的值为2 C. 的值可以为 D. 的值可以为 10.
气象意义上从春季进入夏季的标志为“连续5天的日平均温度均不低于 ”.现有甲、乙、丙三地连续5
天的日平均温度(单位: )的记录数据(记录数据都是正整数):
学科网(北京)股份有限公司①甲地:5个数据中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体平均数为24;
③丙地:5个数据中有一个数据是32,总体平均数为26,总体方差为10.8,
则肯定进入夏季的地区有
A.一个都没有 B.甲地 C.乙地 D.丙地
11.定义在 上的函数 满足 , 是偶函数, ,则
A. 是奇函数 B.
C. 的图象关于直线 对称 D.
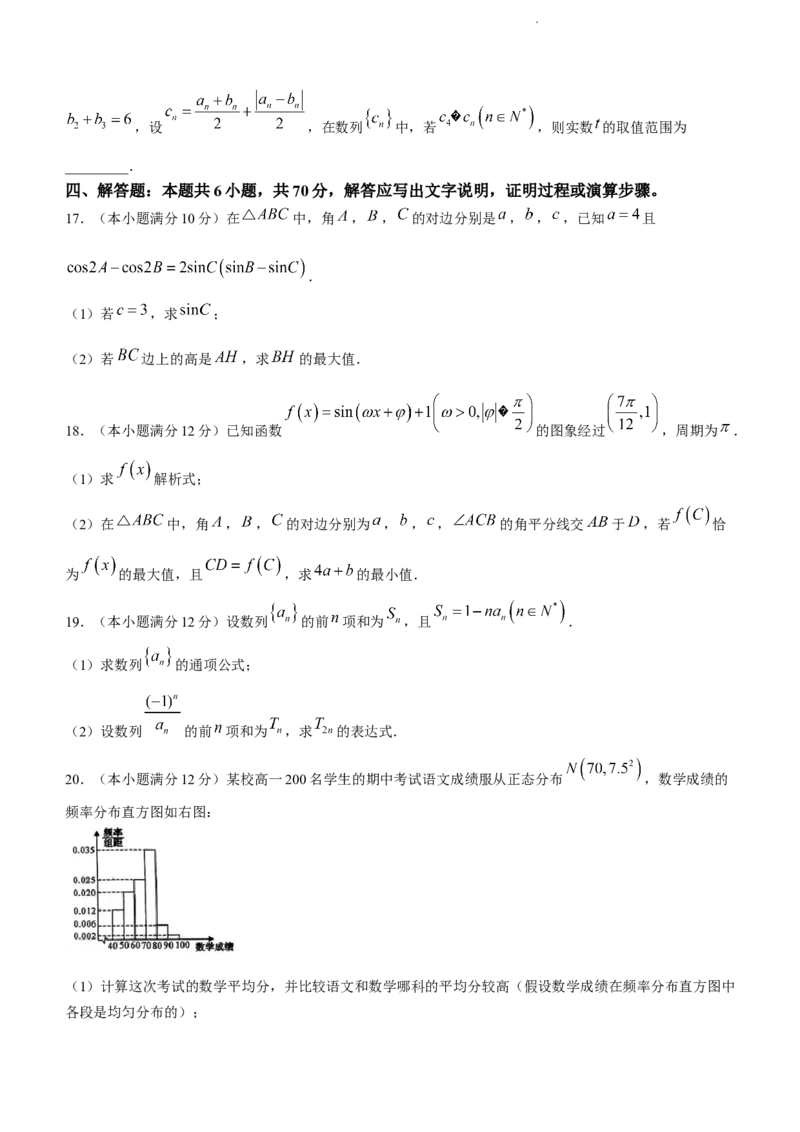
12.如图,双曲线 的左右顶点为 , , 为 右支上一
点(不包含顶点), , , ,直
线 与双曲线 的渐近线交于 、 , 为线段 的 中点,则
A.双曲线 的离心率为
B. 到两条渐近线的距离之积为
C.
D.若直线 与 的斜率分别为 , ,则
第Ⅱ卷
三、填空题:本题共4小题,每小题5分,共20分,请将答案填在答题卡对应题号的位置上.
13.若 的展开式中 的系数为15,则 _________.
14.已知直线 的倾斜角为 ,则 的值是_________.
15.已知函数 若方程 恰有两个不同的实数根 , ,则 的最大值是
_________.
16.已知数列 通项公式为 ,数列 为公比小于1的等比数列,且满足 ,
学科网(北京)股份有限公司,设 ,在数列 中,若 ,则实数 的取值范围为
_________.
四、解答题:本题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)在 中,角 , , 的对边分别是 , , ,已知 且
.
(1)若 ,求 ;
(2)若 边上的高是 ,求 的最大值.
18.(本小题满分12分)已知函数 的图象经过 ,周期为 .
(1)求 解析式;
(2)在 中,角 , , 的对边分别为 , , , 的角平分线交 于 ,若 恰
为 的最大值,且 ,求 的最小值.
19.(本小题满分12分)设数列 的前 项和为 ,且 .
(1)求数列 的通项公式;
(2)设数列 的前 项和为 ,求 的表达式.
20.(本小题满分12分)某校高一200名学生的期中考试语文成绩服从正态分布 ,数学成绩的
频率分布直方图如右图:
(1)计算这次考试的数学平均分,并比较语文和数学哪科的平均分较高(假设数学成绩在频率分布直方图中
各段是均匀分布的);
学科网(北京)股份有限公司(2)如果成绩大于85分的学生为优秀,这200名学生中本次考试语文、数学优秀的人数大约各多少人?
(3)如果语文和数学两科都优秀的共有4人,从(2)中的这些同学中随机抽取3人,设三人中两科都优秀
的有 人,求 的分布列和数学期望.
附参考公式:若 ,则
,
21.(本小题满分12分)已知椭圆 的离心率为 ,左、右顶点分别为 、 ,
点 、 为椭圆上异于 、 的两点, 面积的最大值为2.
(1)求椭圆 的方程;
(2)设直线 、 的斜率分别为 、 ,且 .
①求证:直线 经过定点.
②设 和 的面积分别为 、 ,求 的最大值.
22.(本小题满分12分)已知函数 .
(1)若函数 在 上为增函数,求实数 的最大值;
(2)若 有两个极值点 ,且不等式 恒成立,求正数 的取值范围(
为自然对数的底数).
2023-2024 学年普通高中高三第二次教学质量检测
数学参考答案
一、选择题
1.B 2.D 3.D 4.C 5.A 6.C 7.D 8.B
二、选择题
9.AD 10.BD 11.ABD 12.ACD
三、填空题
学科网(北京)股份有限公司13.3 14. 15. 16.
四、解答题
17.解:(1)由 可得:
,
即: .
即 ,又 , ,
由正弦定理得: .
(2)由题意,
,
,
时, 取得最大值 .
18.解:(1) 周期为 , ,
图象经过 , ,
,又 ,
学科网(北京)股份有限公司,
(2) 的最大值2,
,得 ,
, , ,
,
,
,即 ,
,
,当且仅当 ,即 时取等号,
又 ,即当且仅当 , 时取等号,
所以 的最小值为 .
19.解:(1)当 时, ,所以 .
当 时, , .
两式相减得: ,即 .
故 .
学科网(北京)股份有限公司故 .
(2)令 ,
则
,
为等差数列.
.
20.解:(1)数学成绩的平均分为
,
根据语文成绩的正态分布知语文平均分为70分,所以语文平均分高些.
(2)因为语文成绩优秀的概率为 ,
数学成绩优秀的概率为 ,
所以语文成绩优秀人数为 ,数学成绩优秀人数为 .
(3)语文数学两科都优秀的有4人,单科优秀的有6人, 所有可能的取值为0,1,2,3.
, , , .
的分布列为
0 1 2 3
所以 的数学期望 .
21.解:(1)当点 为椭圆 短轴顶点时, 的面积取最大值,
学科网(北京)股份有限公司且最大值为 ,
由题意可得 ,解得 ,所以,椭圆 的标准方程为 .
(2)①设点 、 .
若直线 的斜率为零,则点 、 关于 轴对称,则 ,不合乎题意.
设直线 的方程为 ,由于直线 不过椭圆 的左、右顶点,则 ,
联立 可得 ,
,可得 ,
由韦达定理可得 , ,则 ,
所以
,解得 ,
即直线 的方程为 ,故直线 过定点 .
②由韦达定理可得 , ,
所以,
学科网(北京)股份有限公司,
,则 ,
因为函数 在 上单调递增,
故 ,
所以, ,当且仅当 时,等号成立,
因此, 的最大值为 .
22.解:(1) , ,
因为函数 在 上为增函数,
所以 , 恒成立,即 , 恒成立,
记 ,则 ,由 ,由 ,
所以 在 上递增,在 上递减,又当 时, ,
所以 ,即实数 的最大值为 ;
(2)因为 是 的两个极值点,所以 , 是方程 的两个实数根,
学科网(北京)股份有限公司由 .
因为 ,两边取自然对数得 ,
即 ,
令 ,则 在 恒成立,
所以 在 恒成立,
令 ,则 .
①当 ,即 时, , 在 上递增,所以 恒成立,满足题意;
②当 时, 在 上递增,在 上递减,
所以当 时, ,
所以, 在 不能恒成立,不满足题意,
综上, 的取值范围是 .
学科网(北京)股份有限公司