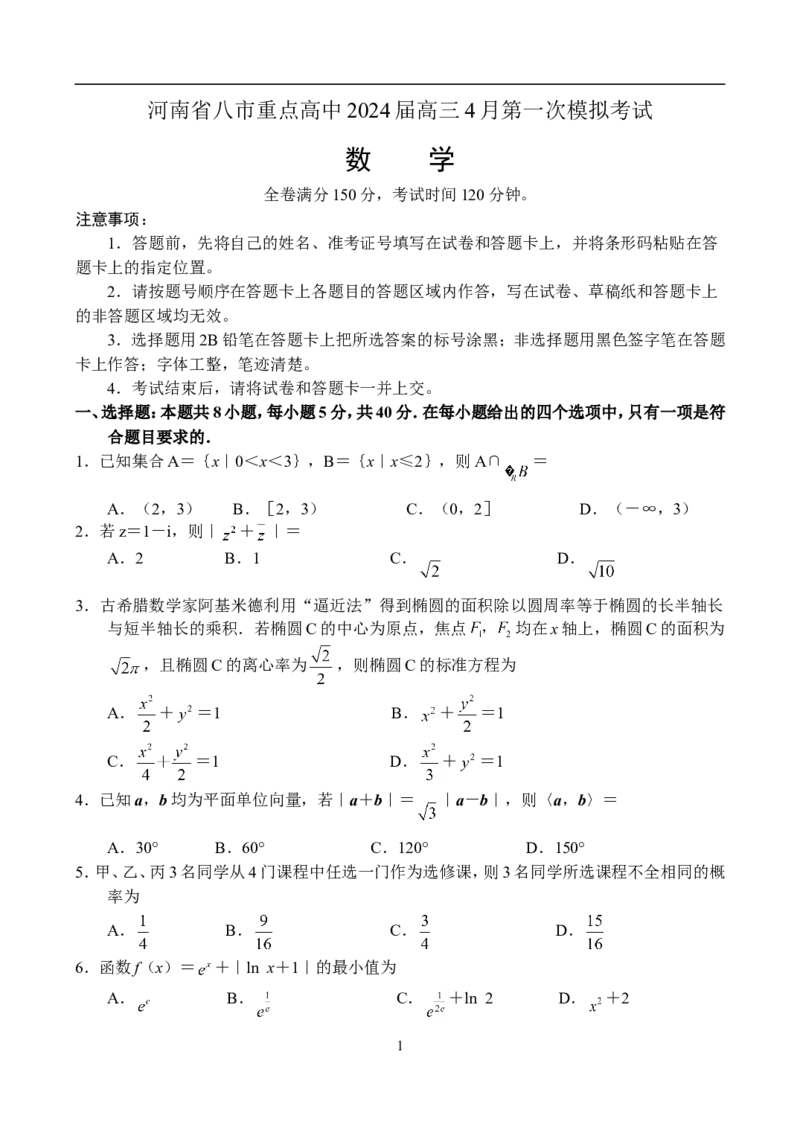文档内容
河南省八市重点高中2024届高三4月第一次模拟考试
数 学
全卷满分150分,考试时间120分钟。
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将条形码粘贴在答
题卡上的指定位置。
2.请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷、草稿纸和答题卡上
的非答题区域均无效。
3.选择题用2B铅笔在答题卡上把所选答案的标号涂黑;非选择题用黑色签字笔在答题
卡上作答;字体工整,笔迹清楚。
4.考试结束后,请将试卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.已知集合A={x|0<x<3},B={x|x≤2},则A∩ =
A.(2,3) B.[2,3) C.(0,2] D.(-∞,3)
2.若z=1-i,则| + |=
A.2 B.1 C. D.
3.古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长
与短半轴长的乘积.若椭圆C的中心为原点,焦点 均在x轴上,椭圆C的面积为
,且椭圆C的离心率为 ,则椭圆C的标准方程为
A. + =1 B. + =1
C. =1 D. + =1
4.已知a,b均为平面单位向量,若|a+b|= |a-b|,则〈a,b〉=
A.30° B.60° C.120° D.150°
5.甲、乙、丙3名同学从4门课程中任选一门作为选修课,则3名同学所选课程不全相同的概
率为
A. B. C. D.
6.函数f(x)= +|ln x+1|的最小值为
A. B. C. +ln 2 D. +2
17.记数列{ }的前n项和为 ,已知 =2,{ }为等差数列,若 + + =1,则 =
A.2 B.-2 C. D.
8.在正方体ABCD- 中, =4,P为 的中点,E在棱 上,且 = ,
则过E且与 垂直的平面截正方体ABCD- 所得截面的面积为
A.6 B.8 C.12 D.16
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.为提高学生的消防安全意识,某学校组织一次消
防安全知识竞赛,已知该校高一、高二、高三三
个年级的人数之比为1:2:3,根据各年级人数
采用分层抽样随机抽取了样本容量为n的部分
考生成绩,并作出如图所示的频率分布直方图,
成绩前10%的学生授予“安全标兵”称号,已
知成绩落在区间[50,60)的人数为24,则
A.n=150
B.估计样本中高三年级的人数为75
C.估计安全知识竞赛考生的平均分为73
D.估计成绩84分以上的学生将获得“安全标兵”称号
10.已知函数f(x)=sin( + )+B( >0,0< < ),( ,1),( ,1)为
f(x)的两个相邻的对称中心,则
A.f(x)的最小正周期为
B.f(x)的最大值为1
C.直线x= 是曲线y=f(x)的一条对称轴
D.将f(x)的图象向右平移 个单位长度,所得图象关于原点对称
11.已知函数f(x)的定义域为R,f(x+y)-f(x-y)=f(x+ )f(y+ ),f(0)≠0,则
A.f( )=0 B.f(0)=-2
C.f(x)的一个周期为3 D. =2
三、填空题:本题共3小题,每小题5分,共15分.
212.若sin -2cos =0,则 =_______.
13.在正四棱台 -ABCD中, ∥平面 ,AB= =4,则正四棱台
-ABCD的体积为_______.
14.已知双曲线C: (a>0,b>0)的左、右焦点分别为 ,焦距为2c,A,B为C
上的两点,AB∥ ,四边形 的面积为 (2a+c)b,若 的周长为10a,
则C的离心率为_______.
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.
15.(本小题满分13分)
不透明的袋子中装有3个黑球,2个红球,1个白球,从中任意取出2个球,再放入1个红
球和1个白球.
(1)求取球放球结束后袋子里白球的个数为2的概率;
(2)设取球放球结束后袋子里红球的个数为随机变量X,求X的分布列以及数学期望.
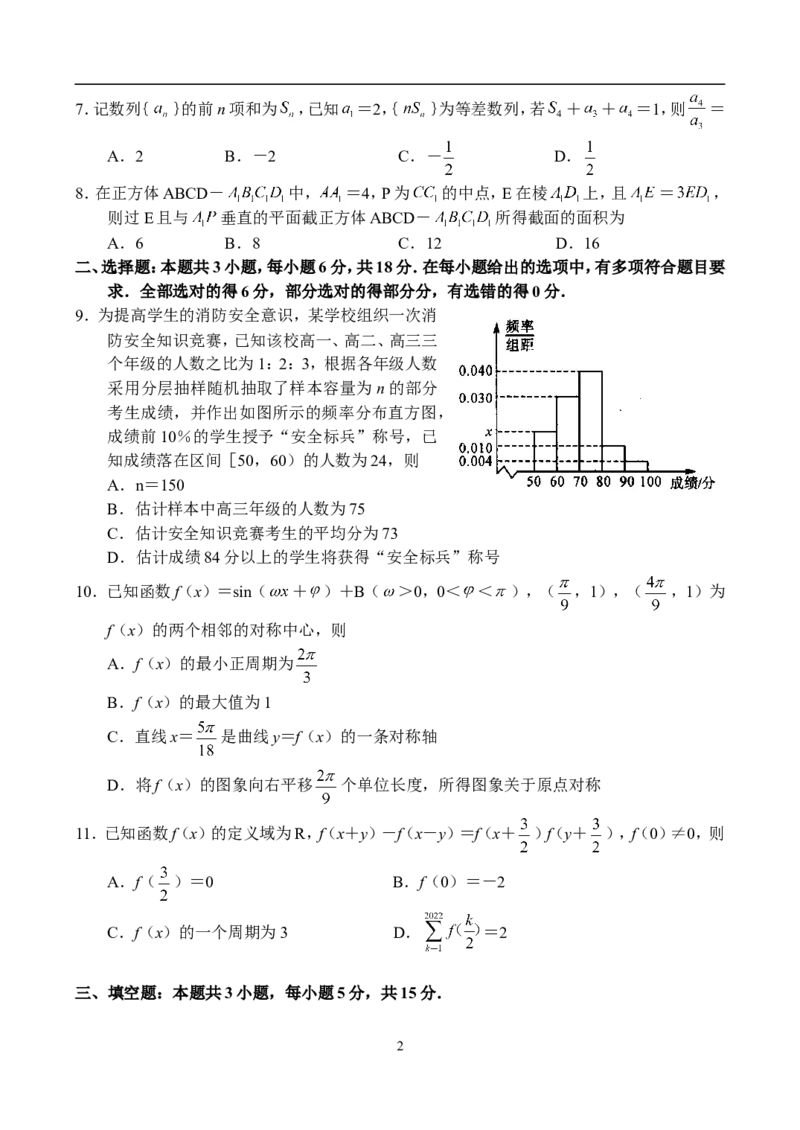
16.(本小题满分15分)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,CD⊥AD,AB=2,PA=AD=
CD=1,E为PB的中点.
(1)证明:BC⊥平面PAC;
(2)求二面角D-EC-B的余弦值.
17.(本小题满分15分)
记 分别为数列{ },{ }的前n项和, + =2, + = , = .
(1)求数列{ },{ }的通项公式;
(2)设 = 记{ }的前n项和为 ,若对任意n∈ , <m,求整数m的最
小值.
18.(本小题满分17分)
设P为抛物线C: =4y准线上的一个动点,过P作C的两条切线,切点分别为A,B.
(1)证明:直线AB过定点;
(2)当直线AB斜率不为0时,直线AB交C的准线于M,设Q为线段AB的中点,求
△QPM面积的最小值.
19.(本小题满分17分)
3已知函数f(x)= -rx-1(x>-1),r>0且r≠1.
(1)讨论f(x)的单调性;
(2)比较 与 的大小,并说明理由;
(3)当n∈ 时,证明: <n+ .
4