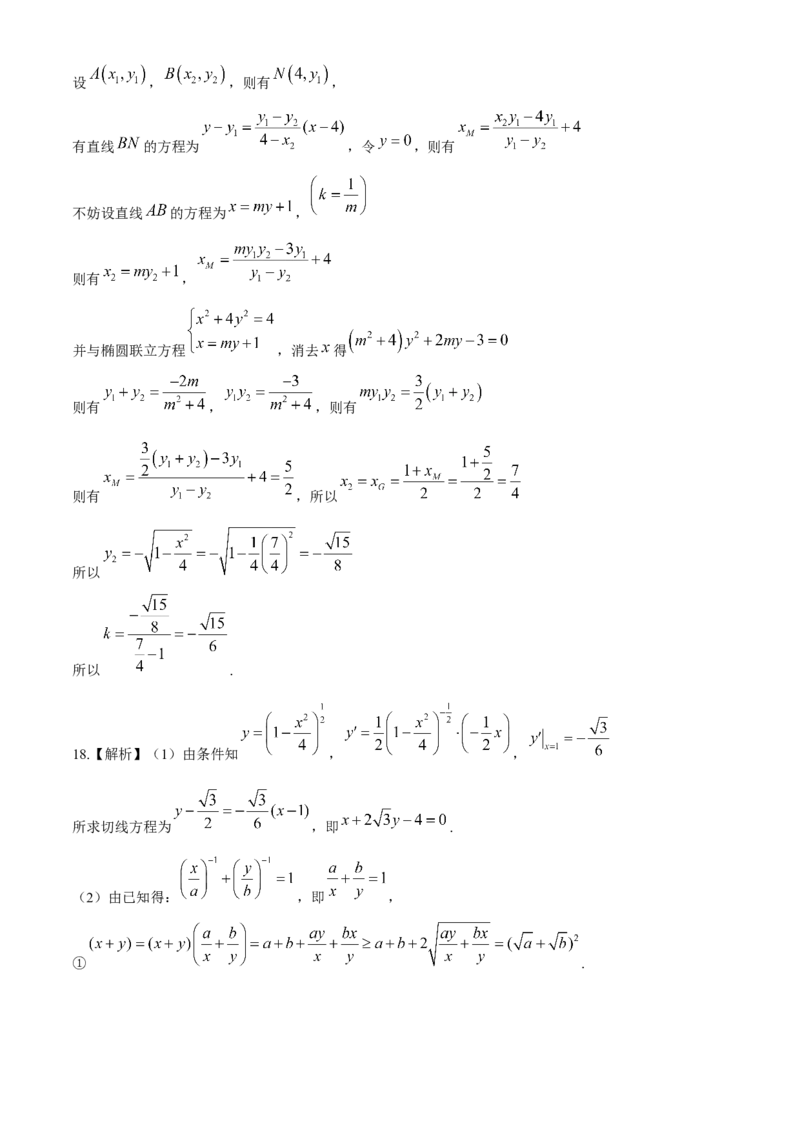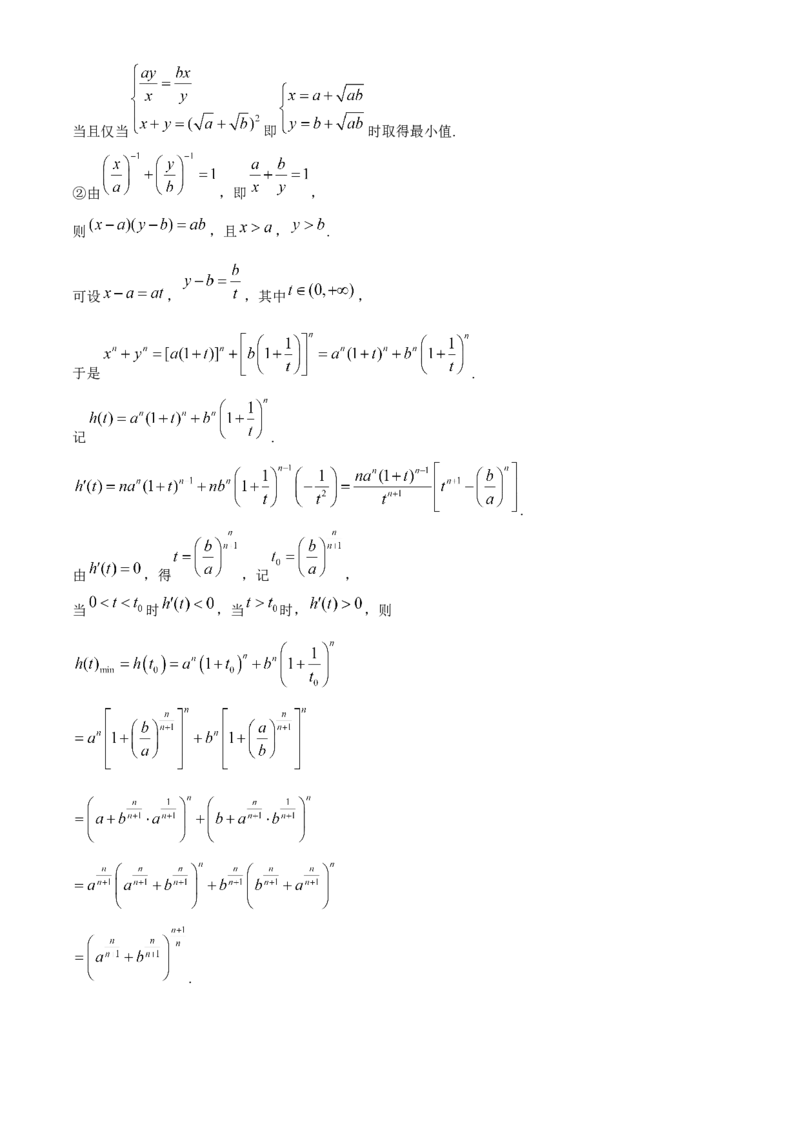文档内容
2024 届高三第三次模拟测试
数学试题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合 , .则 ( )
A. B. C. D.
2.已知 “ ”, “ ”,若 是 的充分不必要条件,则实数 的取值范围是(
)
A. B. C. D.
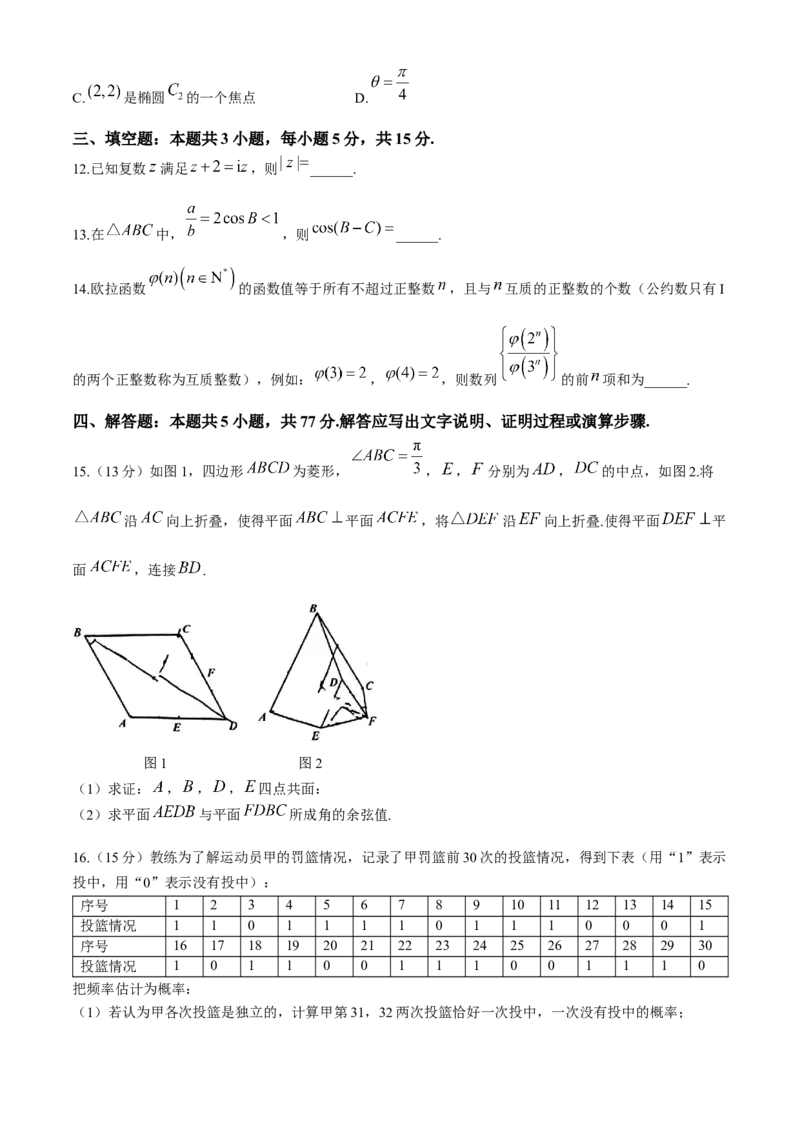
3.如图对两组数据 , 和 , 分别进行回归分析,得到散点图如图,并求得线性回归方程分别是
和 ,并对变量 , 进行线性相关检验,得到相关系数 ,对变量 , 进行线
性相关检验,得到相关系数 ,则下列判断正确的是( )
A. B. C. D.
4.已知 , , ,则 , , 的大小关系是( )
A. B. C. D.
5.已知三棱锥 中, 是边长为2的正三角形, 是以 为斜边的等腰直角三角形,
分别是线段 的中点,若 ,则三棱锥 的外接球的表面积为( )
A. B. C. D.
6.已知数列 的前 项和为 ,且满足 , ,则 的值不可能是( )
学科网(北京)股份有限公司A.1 B.2 C.3 D.15
7.已知双曲线 的左、右焦点分别为 , .过 作直线 与双曲线 的右支交
于 , 两点,若 的周长为 ,则双曲线 的离心率的取值范围是( )
A. B. C. D.
8.已知函数 .则下列说法中错误的是( )
A.当 时, 在 上单调递增
B.当 时, 的最小值是一个与 无关的常数
C. 可能有三个不同的零点
D.当 时, 有且仅有一个零点
二、选择题:本题共3小题,每题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知 是单调递减的等比数列,若 ,前3项和 ,则下列说法中正确的是( )
A. B. C. D.
10.已知函数 ,若 的图象关于直线 对称,则下列说法
正确的是( )
A. 的图象也关于直线 对称 B. 的图象关于 中心对称
C. D.
11.是椭圆 上所有的点绕原点旋转 角,得到椭圆 的方程:
,则下列说法中正确的是( )
A. B.椭圆 的离心率为
学科网(北京)股份有限公司C. 是椭圆 的一个焦点 D.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知复数 满足 ,则 ______.
13.在 中, ,则 ______.
14.欧拉函数 的函数值等于所有不超过正整数 ,且与 互质的正整数的个数(公约数只有I
的两个正整数称为互质整数),例如: , ,则数列 的前 项和为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
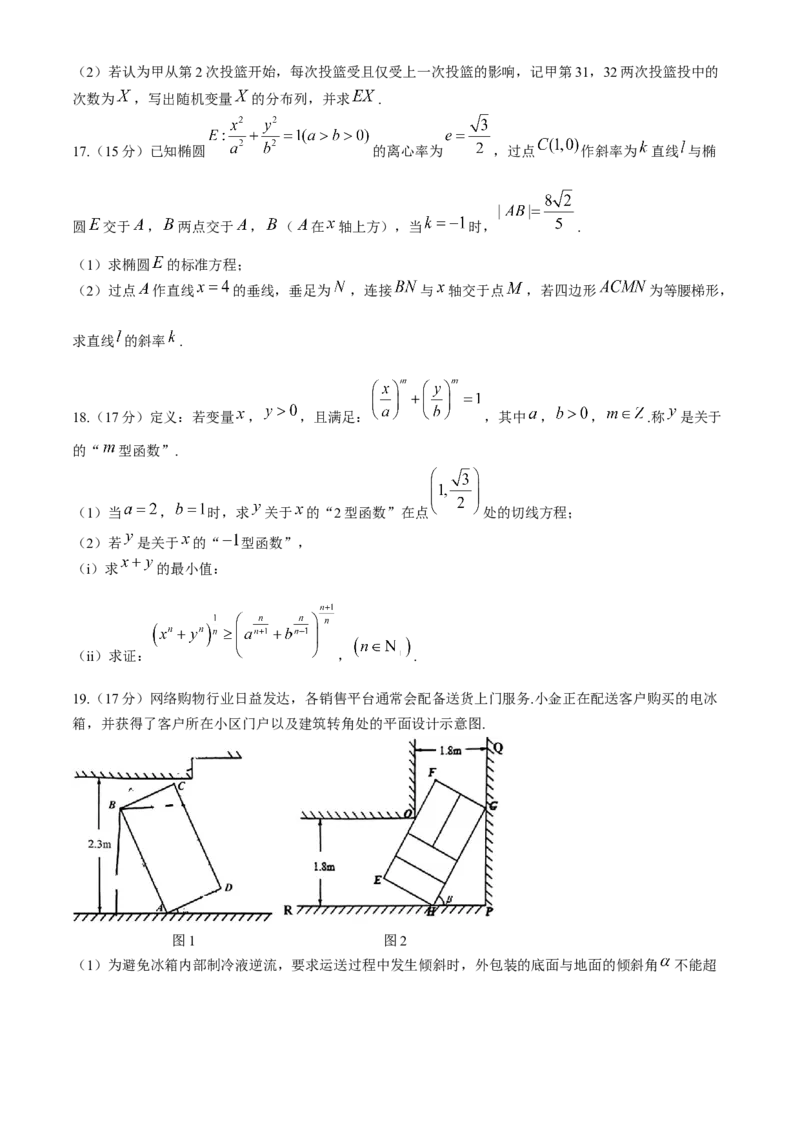
15.(13分)如图1,四边形 为菱形, , , 分别为 , 的中点,如图2.将
沿 向上折叠,使得平面 平面 ,将 沿 向上折叠.使得平面 平
面 ,连接 .
图1 图2
(1)求证: , , , 四点共面:
(2)求平面 与平面 所成角的余弦值.
16.(15分)教练为了解运动员甲的罚篮情况,记录了甲罚篮前30次的投篮情况,得到下表(用“1”表示
投中,用“0”表示没有投中):
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
投篮情况 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1
序号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
投篮情况 1 0 1 1 0 0 1 1 1 0 0 1 1 1 0
把频率估计为概率:
(1)若认为甲各次投篮是独立的,计算甲第31,32两次投篮恰好一次投中,一次没有投中的概率;
学科网(北京)股份有限公司(2)若认为甲从第2次投篮开始,每次投篮受且仅受上一次投篮的影响,记甲第31,32两次投篮投中的
次数为 ,写出随机变量 的分布列,并求 .
17.(15分)已知椭圆 的离心率为 ,过点 作斜率为 直线 与椭
圆 交于 , 两点交于 , ( 在 轴上方),当 时, .
(1)求椭圆 的标准方程;
(2)过点 作直线 的垂线,垂足为 ,连接 与 轴交于点 ,若四边形 为等腰梯形,
求直线 的斜率 .
18.(17分)定义:若变量 , ,且满足: ,其中 , , .称 是关于
的“ 型函数”.
(1)当 , 时,求 关于 的“2型函数”在点 处的切线方程;
(2)若 是关于 的“ 型函数”,
(i)求 的最小值:
(ii)求证: , .
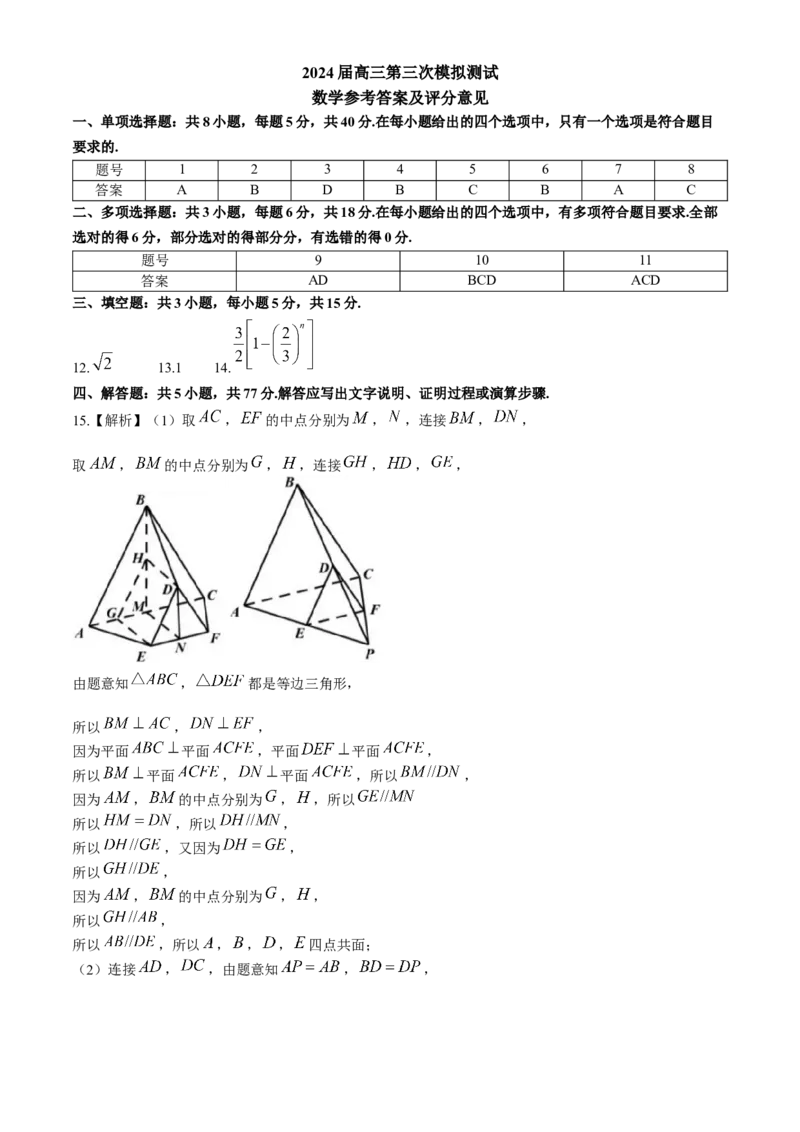
19.(17分)网络购物行业日益发达,各销售平台通常会配备送货上门服务.小金正在配送客户购买的电冰
箱,并获得了客户所在小区门户以及建筑转角处的平面设计示意图.
图1 图2
(1)为避免冰箱内部制冷液逆流,要求运送过程中发生倾斜时,外包装的底面与地面的倾斜角 不能超
学科网(北京)股份有限公司过 ,且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形
, , ,而客户家门高度为2.3米,其他过道高度足够,若以倾斜角
的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.
(2)由于客户选择以旧换新服务,小金需要将客户长方体形状的旧冰箱进行回收,为了省力,小金选择
将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上,平板车长宽均小于冰箱背面),推运过程中遇
到一处直角过道,如图2所示,过道宽为1.8米.,记此冰箱水平截面为矩形 , .设
,当冰箱被卡住时(即点 、 分别在射线 、 上,点 在线段 上),尝试用
表示冰箱高度 的长,并求出 的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其
高度的最大值是多少?(结果精确到 )
学科网(北京)股份有限公司2024届高三第三次模拟测试
数学参考答案及评分意见
一、单项选择题:共8小题,每题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目
要求的.
题号 1 2 3 4 5 6 7 8
答案 A B D B C B A C
二、多项选择题:共3小题,每题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
题号 9 10 11
答案 AD BCD ACD
三、填空题:共3小题,每小题5分,共15分.
12. 13.1 14.
四、解答题:共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.【解析】(1)取 , 的中点分别为 , ,连接 , ,
取 , 的中点分别为 , ,连接 , , ,
由题意知 , 都是等边三角形,
所以 , ,
因为平面 平面 ,平面 平面 ,
所以 平面 , 平面 ,所以 ,
因为 , 的中点分别为 , ,所以
所以 ,所以 ,
所以 ,又因为 ,
所以 ,
因为 , 的中点分别为 , ,
所以 ,
所以 ,所以 , , , 四点共面;
(2)连接 , ,由题意知 , ,
学科网(北京)股份有限公司所以 ,同理 ,
所以 就是二面角 的平面角,
设 ,则 , , ,
所以 ,同理 ,
所以 ,
所以平面 与平面 所成角的余弦值为 .
16.【解析】(1)根据表中的数据,在甲前30次的投篮过程中,有19次投中,11次没有投中,因此因动
员甲投篮投中的概率 ,投不中的概率为 ,若甲各次投篮互相独立,那么第31,32次投篮,
恰有一次投中,一次没有投中的概率为 ;
(2)根据表格中的数据可以知道:上一次投篮投中,这一次也投中的概率为 ,
上一次投篮没有投中,这一次投篮投中的概率为 ,
的所有可能取值为 , , ,且由表格可知第30次运动员甲没有投中,
则 ,
学科网(北京)股份有限公司,
,
所以随机变量 的分布列为:
0 1 2
所以 .
17.【解析】(1)因为 ,所以 ,即 ,
不防设椭圆的方程为 ,即 .
并与直线 联立方程
消去 得
设 , ,则有 ,
由
所以 ,即
所以椭圆 的标准方程为 ;
(2)因为四边形 为等腰梯形,则必有 ,
即 ,不妨设 的中点为 ,则必有 ,
要求直线 的斜率,只需要转化为求点 的坐标,则有
学科网(北京)股份有限公司设 , ,则有 ,
有直线 的方程为 ,令 ,则有
不妨设直线 的方程为 ,
则有 ,
并与椭圆联立方程 ,消去 得
则有 , ,则有
则有 ,所以
所以
所以 .
18.【解析】(1)由条件知 , ,
所求切线方程为 ,即 .
(2)由已知得: ,即 ,
① .
学科网(北京)股份有限公司当且仅当 即 时取得最小值.
②由 ,即 ,
则 ,且 , .
可设 , ,其中 ,
于是 .
记 .
.
由 ,得 ,记 ,
当 时 ,当 时, ,则
.
学科网(北京)股份有限公司所以 .
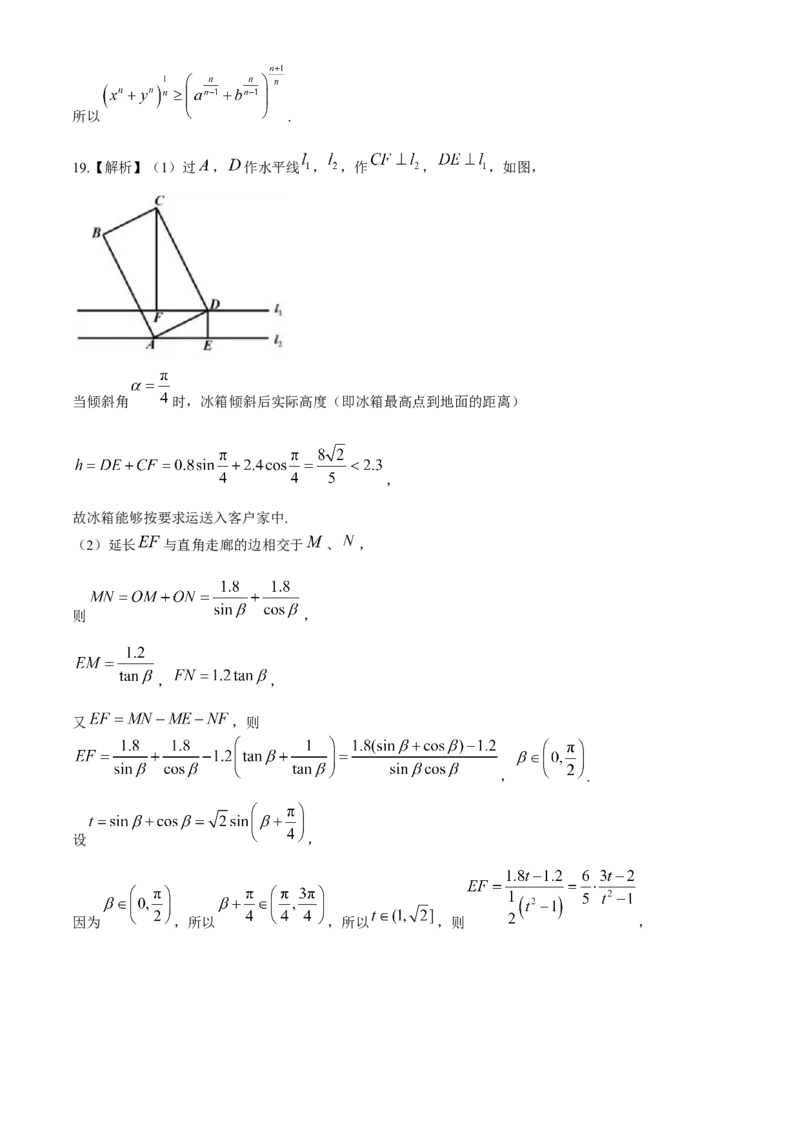
19.【解析】(1)过 , 作水平线 , ,作 , ,如图,
当倾斜角 时,冰箱倾斜后实际高度(即冰箱最高点到地面的距离)
,
故冰箱能够按要求运送入客户家中.
(2)延长 与直角走廊的边相交于 、 ,
则 ,
, ,
又 ,则
, .
设 ,
因为 ,所以 ,所以 ,则 ,
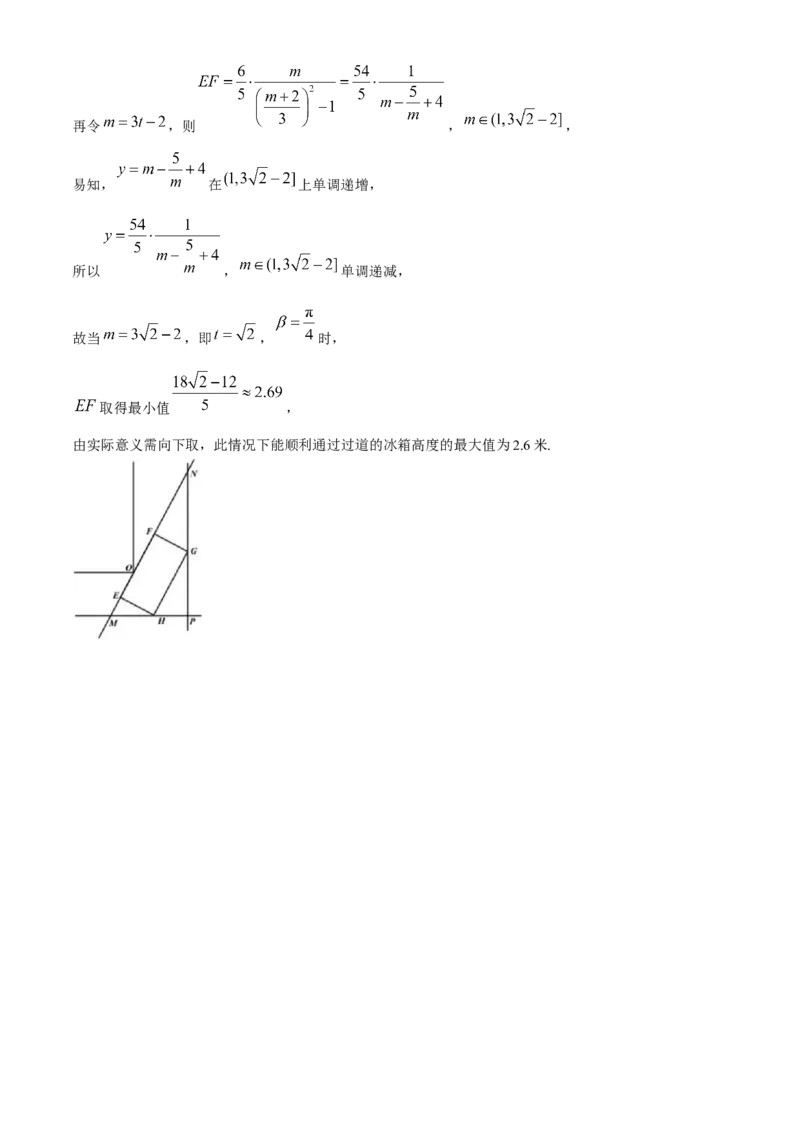
学科网(北京)股份有限公司再令 ,则 , ,
易知, 在 上单调递增,
所以 , 单调递减,
故当 ,即 , 时,
取得最小值 ,
由实际意义需向下取,此情况下能顺利通过过道的冰箱高度的最大值为2.6米.
学科网(北京)股份有限公司