江苏泰州2024届高三2月调研测试数学试题+答案(1)_2024年3月_013月合集_2024届新高考19题（九省联考模式）数学合集140套

泰州市 2024 届高三调研测试 数学试题 （考试时间：120分钟；总分：150分） 一、单项选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有 一项是符合题目要求的． 1．有一组样本数据9，4，5，7，8，2，则样本中位数为（ ） A．5 B．6 C．7 D．8 2．已知{ a }为等差数列，若m，n，p，q是正整数，则m+n= p+q是a +a =a +a 的（ ） n m n p q A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分不必要条件 3．每袋食盐的标准质量为500克，现采用自动流水线包装食盐，抽取一袋食盐检测，它的实际质量与标准质 量存在一定的误差，误差值为实际质量减去标准质量．随机抽取100袋食盐，检测发现误差X（单位：克） 近似服从正态分布N ( 0,σ2 ) ，P ( X ≥2 )=0.02，则X介于－2~2的食盐袋数大约为（ ） A．4 B．48 C．50 D．96      4．若e ，e 是夹角为60°的两个单位向量，则向量e −e 与e 的夹角为（ ） 1 2 1 2 2 A．30° B．60° C．90° D．120° eaxsinx 5．已知函数 f ( x )= 是定义在R上的奇函数，则实数a=（ ） 1+ex 1 A．－1 B．0 C． D．1 2 6．若复数z满足 z−1 = z+i ，则 z−1 的最小值为（ ） 1 2 A． B． C．1 D． 2 2 2 y2 7．已知点P ( x ,y )在双曲线x2 − =1 ( b>0 )上，过点P作双曲线的渐近线的垂线，垂足分别为A，B， 0 0 b2   21 若x >1，PA⋅PB= ，则b=（ ） 0 32 A． 3 B．2 C． 7 D．2 2 π ( )  π 8．在△ABC中，角A，B，C的对边分别为a，b，c，若A= ， 3−1 sinC = 2tan AsinC+  ， 10  4 则（ ） A．c2c 学科网（北京）股份有限公司二、选择题：本题共 3小题，每小题 6分，共 18分．在每小题给出的选项中，有多项符合题 目要求．全部选对的得 6分，部分选对的得部分分，有选错的得 0分． 9．已知函数 f ( x )=sin2x+2sin2 x，则（ ） π  A．函数 f ( x )的图象关于点  ,0 对称 8   π B．函数 f ( x )在区间 0,  上单调递增  4 3π C．函数 f ( x )的图象向左平移 个单位长度所得到的图象所对应的函数为偶函数 8 D．函数 f ( x )在区间(−π,π )上恰有3个零点 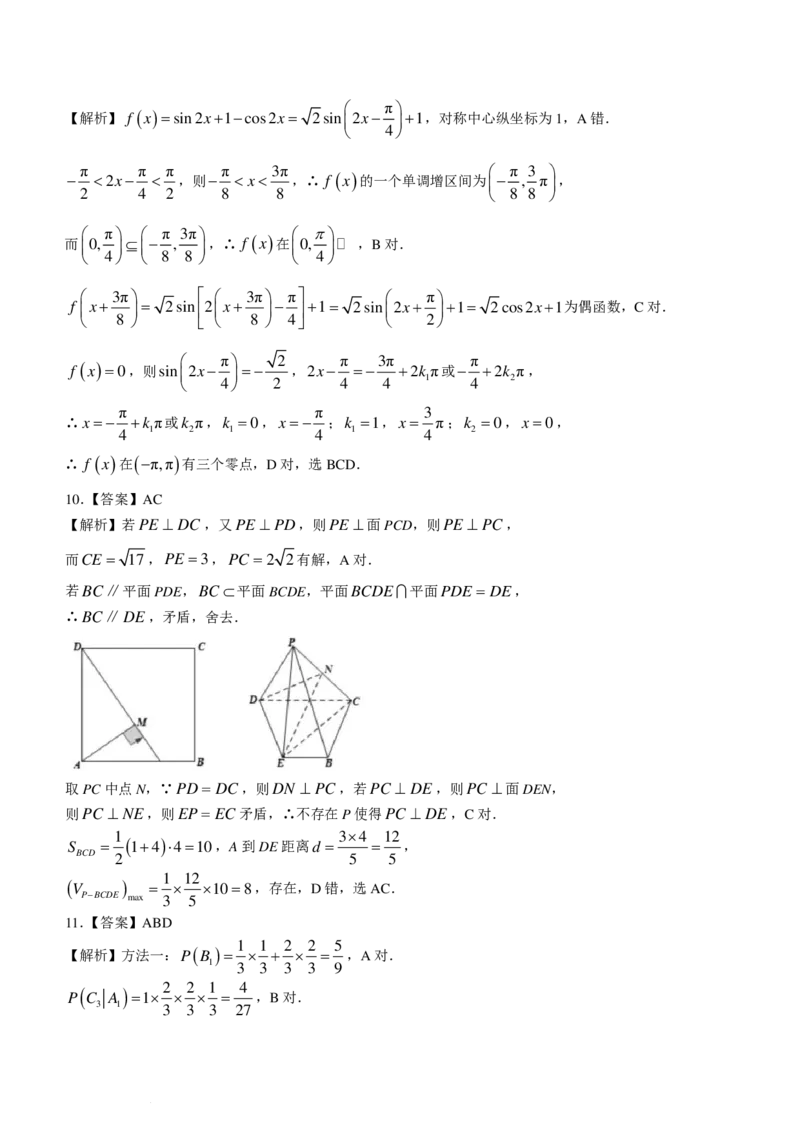10．已知正方形ABCD的边长为4，点E在线段AB上，BE =1．沿DE将△ADE折起，使点A翻折至平 面BCDE外的点P，则（ ） A．存在点P，使得PE ⊥ DC B．存在点P，使得直线BC∥平面PDE C．不存在点P，使得PC ⊥ DE D．不存在点P，使得四棱锥P−BCDE的体积为8 11．甲、乙两个口袋各装有1个红球和2个白球，这些球除颜色外完全相同．把从甲、乙两个口袋中各任取 一个球放入对方口袋中称为一次操作，重复n次操作后，甲口袋中恰有0个红球，1个红球，2个红球分别记 为事件A ，B ，C ，则（ ） n n n 5 4 2 55 A．P ( B )= B．P ( C A ) = C．P ( BC )= D．P ( A +B )= 1 9 3 1 27 1 2 81 1 2 81 三、填空题：本题共 3小题，每小题 5分，共 15分． 12．已知集合A= {( x,y ) x+ y =2 } ，B= { ( x,y ) ( x−1 )2 + y2 =1 } ，则AB中元素的个数为______． x2 y2 13．在平面直角坐标系xOy中，椭圆 + =1 ( a >b>0 )的左焦点为F，点P在椭圆上，PF的中点为 a2 b2 Q，若OQ⊥ PF ，PF = 3OP，则椭圆离心率的值为______． 14．将“用一条线段联结两个点”称为一次操作，把操作得到的线段称为“边”．若单位圆上n个颜色各不相 同的点经过k次操作后，从任意一点出发，沿着边可以到达其他任意点，就称这n个点和k条边所构成的图 形满足“条件T”，并将所有满足“条件T”的图形个数记为T ( n,k )，则T ( 5,4 )=______． 四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤． 15．（13分）已知函数 f ( x )= x4 +ax3，x∈R． （1）若函数在点 ( 1, f ( 1 )) 处的切线过原点，求实数a的值； （2）若a =−4，求函数 f ( x )在区间[−1,4 ]上的最大值． 学科网（北京）股份有限公司16．（15分）某游戏设置了两套规则，规则A：抛掷一颗骰子n次，若n次结果向上的点数之和大于2时， 继续下一次抛掷，否则停止抛掷；规则B：抛掷一颗骰子一次，结果向上的点数大于2时，继续下一次抛 掷，否则停止抛掷． （1）若执行规则A，求抛掷次数恰为1次的概率； （2）若执行规则B，证明：抛掷次数的数学期望不大于3． 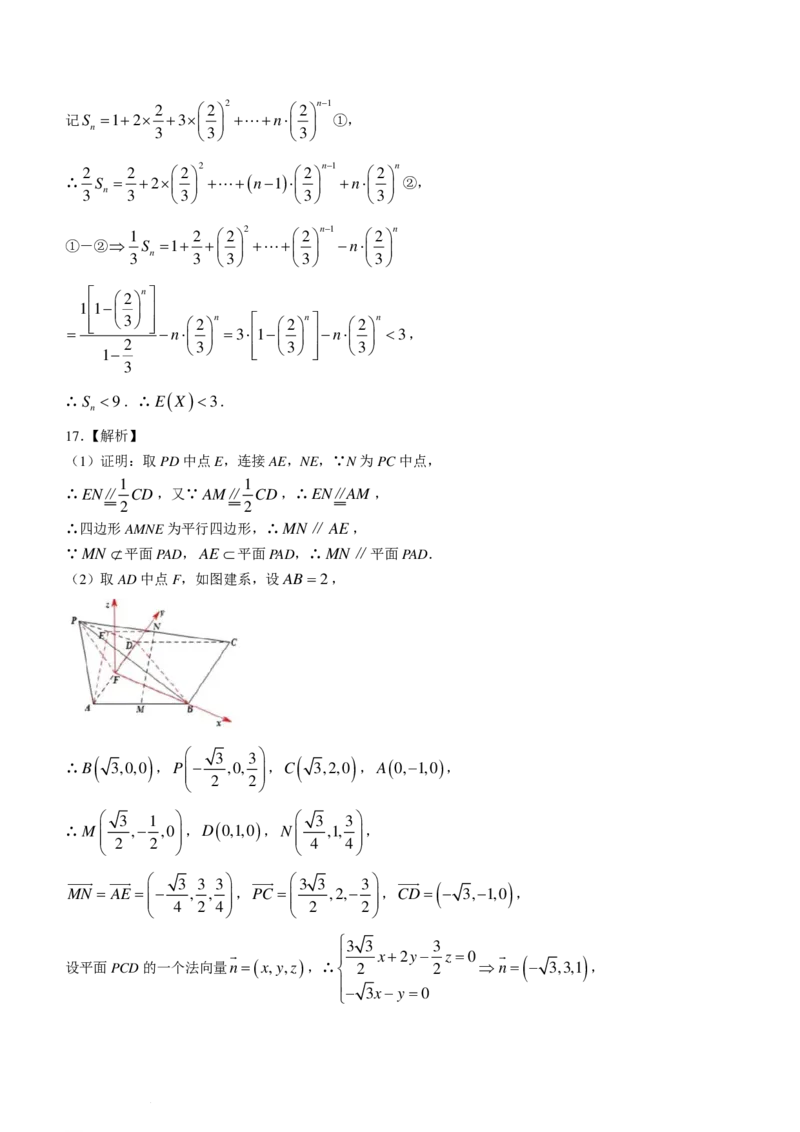17．（15分）如图，在四棱锥P−ABCD中，底面ABCD是菱形，∠BAD=60°，△PAD为等边三角形， 点M，N分别为AB，PC的中点． （1）证明：直线MN∥平面PAD； （2）当二面角P−AD−C为120°时，求直线MN与平面PCD所成的角的正弦值． 18．（17分）已知抛物线E：x2 =2y，焦点为F，过F作y轴的垂线l ，点P在x轴下方，过点P作抛物线 0 E的两条切线l ，l ，l ，l 分别交x轴于A，B两点，l ，l 分别交l 于C，D两点． 1 2 1 2 1 2 0 （1）若l ，l 与抛物线E相切于C，D两点，求点P的坐标； 1 2 （2）证明：△PAB的外接圆过定点； （3）求△PCD面积S的最小值． 2a −1 a +1 19．（17分）已知数列{ a }满足 n+1 + n =2，n∈N*． n a 2a n n+1 （1）已知a >0， n ①若a =1，求a ； 3 1 ②若关于m的不等式a <1的解集为M，集合M中的最小元素为8，求a 的取值范围； m 1 1 （2）若a = ，是否存在正整数k ( k ≥2 )，使得a =a ，若存在，求出k的最小值，若不存在，请说明 1 11 k 1 理由． 泰州市 2024 届高三调研测试 数学参考答案 （考试时间：120分钟；总分：150分） 一、单项选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有 学科网（北京）股份有限公司一项是符合题目要求的． 1．【答案】B 5+7 【解析】2，4，5，7，8，9，中位数 =6，选B． 2 2．【答案】A 【解析】m+n= p+q时，a +a =a +( m−1 ) d +a +( n−1 ) d m n 1 1 =2a +( m+n−2 ) d =2a +( p+q−2 ) d =a +( p−1 ) d +a +( q−1 ) d =a +a ， 1 1 1 1 p q 充分a +a =a +a 时，( m+n−2 ) d =( p+q−2 ) d， m n p q d =0时，m+n与 p+q不一定相等，不必要，选A． 3．【答案】D 【解析】X ∼ N ( 0,σ2 ) ，P ( X ≥2 )=0.02，则P ( 0< x<2 )=0.48， P (−2< X <2 )=0.96，100×0.96=96，选D． 4．【答案】D      ( ) 2 1 1 【解析】 e −e e =e e −e = −1=− ， 1 2 2 1 2 2 2 2       2 2 1 e −e = e −2e ⋅e +e = 1−2× +1=1， 1 2 1 1 2 2 2    1    ( e −e ) e − 1 2 2 2 1 cos e −e ,e =    = =− ，夹角120°，选D． 1 2 2 e −e e 1×1 2 1 2 2 5．【答案】C eax 【解析】 f ( x )为奇函数，g ( x )= 为偶函数，g (−x )= g ( x )， 1+ex e−ax eax exe−ax eax 1 ∴ = ，∴ = ，x−ax=ax，a= ，选C． 1+e−x 1+ex ex +1 ex +1 2 6．【答案】B 【解析】令z = x+ yi， z−1 = z+i ，∴y =−x， z−1 = ( x−1 )2 + y2 = x2 −2x+1+x2 = 2x2 −2x+1， 1 2 x= 时 z−1 取最小值 ，选B． 2 2 7．【答案】C 学科网（北京）股份有限公司 1 1 y− y =− ( x−x ) 【解析】PA：y− y =− ( x−x )， 0 b 0 ， 0 b 0  y =bx  x +by x= 0 0   b2 +1  x +by bx +b2y  解得 ，A 0 0 , 0 0 ；  bx +b2y  b2 +1 b2 +1  y = 0 0  b2 +1  1 1 y− y = ( x−x ) PB：y− y = ( x−x )， 0 b 0 ， 0 b 0  y =−bx  x −by x= 0 0   b2 +1  x −by −bx +b2y  解得 ，B 0 0 , 0 0 ，  −bx +b2y  b2 +1 b2 +1  y = 0 0  b2 +1  by −b2x bx − y   −by −b2x −bx − y  PA= 0 0 , 0 0 ，PB= 0 0 , 0 0 ，  b2 +1 b2 +1   b2 +1 b2 +1    b4x2 −b2y2 y2 −b2x2 b2⋅b2 b2 21 PA⋅PB= 0 0 + 0 0 = − = ， ( b2 +1 )2 ( b2 +1 )2 ( b2 +1 )2 ( b2 +1 )2 32 b= 7 ，选C． 8．【答案】A ( ) sinA 2 2  【解析】 3−1 sinC = 2  sinC+ cosC，   cosA 2 2  ( ) 3−1 ⋅sinCcosA=sinAsinC+sinAcosC， 3sinCcosA=sinAsinC+sinAcosC+sinCcosA =sinAsinC+sin ( A+C )=sinAsinC+sinB， ( ) b π  7π ( ) sinB= 3cosA−sinA sinC， =2sin −A =2sin ∈ 1, 2 ， c 3  30 ∴c0， x −x =m，由( x +x )2 =( x −x )2 +4x x =m2 −4t2 ≥0， 1 2 1 2 1 2 1 2 1 2 m≥2t，当且仅当x +x =0时等号成立． 1 2 ( )2 ( )2 1 m  1 t2 +1 m t2 +1 t2 +1 ∴S = ⋅ ⋅ 1+  ≥ ≥ ， △PCD 2 2  t2  2  8t2 4t ( )2 ( ) ( )2 ( )( ) t2 +1 1 2 t2 +1 ⋅2t⋅t− t2 +1 t2 +1 3t2 −1 令 f ( t )= ， f′( t )= ⋅ = ， 4t 4 t2 4t2  3  3  f ( t )在0, 上 ； ,+∞上 ，      3   3   3 4 3 ∴ f ( t )≥ f  = ．    3  9 19．【解析】 2a −1 a +1 1 a +1 （1）① 3 + 2 =2⇒ + 2 =2⇒a2 −3a +2=0，∴a =1或2， a 2a a 2 2 2 2 2 3 2 2a −1 a +1 1 a +1 而 2 + 1 =2．若a =1，∴ + 1 =2⇒a =1或2． a 2a 2 a 2 1 1 2 1 3 a +1 若a =2，∴ + 1 =2⇒a =3或4，经检验均符合．∴a =1或2或3或4． 2 a 4 1 1 1 学科网（北京）股份有限公司②由条件知4a2 −2a +a2 +a =4a a ， n+1 n+1 n n n n+1 ∴( 2a −a )2 −( 2a −a )=0，∴( 2a −a )( 2a −a −1 )=0， n+1 n n+1 n n+1 n n+1 n a a +1 1 +1 1 +1 a a +1 a a +1 2 a +2 2 a +3 a = 1 或a = 1 ，a = 1 或 1 或 → 1 或 → 1 2 2 2 2 3 4 4 2 4 2 4 a a +1 a +2 a +3 a +7 a = 1 或 1 ， 1 ， 1 ，…， 1 ， 4 8 8 8 8 8 … a a +1 a +63 a a +1 a +127 a = 1 或 1 ，…， 1 ，a = 1 或 1 ，…或 1 7 26 26 26 8 27 27 27 a +63 1 ≥1 a ,a ,⋅⋅⋅,a ≥1   26 ∴ 1 2 7 ⇒ ⇒1≤a <128． a <1  a 1 8 1 <1 27 a a +1 a +2 a +2k−1−1 （2）a = 1 或 1 ， 1 ，…， 1 ，k ≥2， k 2k−1 2k−1 2k−1 2k−1 a +m′ 1 2k−1−1 令 1 = ，0≤m′≤2k−1−1，m′∈N，∴ =m′， 2k−1 11 11 1 +93 1 当k =11时，m′=93，a = 11 = =a ， 11 210 11 1 ∴存在这样的k，k =11． min 学科网（北京）股份有限公司