文档内容
2024 届高三开年摸底联考
数学试题
1.答卷前,考生务必将自己的姓名、考场号,座位号、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
考试时间为 120分钟,满分 150分
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1 1
1.已知集合A= x x2 − ≤0,B = x ≥1,则AB =( )
4 x
1 1
A.
0,
B.0,
C.( 0,1 ] D.[ 0,1 ]
2 2
3−2ai
2.复数z = ( a∈R )在复平面内对应的点在( )
2i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.命题“∀x< −1,log x2 >0”的否定为( )
2
A.∀x< −1,log x2 ≤0 B.∀x ≥ −1,log x2 >0 C.∃x ≥ −1,log x2 >0 D.∃x<−1,log x2 ≤0
2 2 2 2
x2 y2
4.若双曲线 − =1(a >0,b>0)的实轴长为2,离心率为 3,则双曲线的左焦点F 到一条渐近线的距
a2 b2
离为( )
A. 2 B.2 2 C.1 D.2
5.已知上底面半径为 2 ,下底面半径为2 2的圆台存在内切球(与上、下底面及侧面都相切的球),则该圆
台的体积为( )
14 6π 56π
A.14 6π B.56π C. D.
3 3
6.已知实数m,n满足1>m>n>0,设a =mlnn,b=nlnm,c =nlnn,则( )
A.a =b>c B.a >b>c C.c>a >b D.c>a =b
学科网(北京)股份有限公司2π
7.在△ABC 中,D为边BC上一点,∠DAC = ,AD =4,AB =2BD,且△ADC 的面积为4 3,则
3
sin∠ABD =( )
15− 3 15+ 3 5− 3 5+ 3
A. B. C. D.
8 8 4 4
2n2 2m2
8.已知等差数列{ a }的前n项和为S ,若m ≠n,且a +a = ,a +a = ,则S =( )
n n 1 m m 1 n n m+n
A.(m+n)2 B.−(m+n)2 C.m2 −n2 D.n2 −m2
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.下列说法正确的是( )
A.若随机变量X ∼ B ( 2,0.2 ),则P ( X =2 )=0.2
B.若经验回归方程 y =bx+a中的b>0,则变量x与y正相关
( ) 1 1 1
C.若随机变量ξ∼ N 0,σ2 ,且P ξ<− = p,则P0<ξ< = − p
2 2 2
D.若事件A与B为互斥事件,则A的对立事件与B的对立事件一定互斥
x
10.已知函数 f ( x )=2sinxcos2 ,则以下结论正确的是( )
2
π 3π
A.π为 f ( x )的一个周期 B. f ( x )在 − , 上有2个零点
2 2
π
C. f ( x )在x = − 处取得极小值 D.对∀x ,x ∈R, f ( x )− f ( x ) ≤ 3
3 1 2 2 1
1 3
11.已知定义在R上的函数 y = f ( 2x+2 )为奇函数,且对∀x∈R,都有 f x+ = f −x,定义在R
2 2
上的函数 f′( x )为 f ( x )的导函数,则以下结论一定正确的是( )
7 1
A. f ( x+2 )为奇函数 B. f = f
2 2
1 3
C. f′ = −f′ D. f′( x )为偶函数
2 2
学科网(北京)股份有限公司三、填空题:本题共 3小题,每小题 5分,共 15分.
1
12.小明上学要经过两个有红绿灯的路口,已知小明在第一个路口遇到红灯的概率为 ,若他在第一个路口遇
4
3
到红灯,第二个路口没有遇到红灯的概率为 ,在第一个路口没有遇到红灯,第二个路口遇到红灯的概率为
4
1
,则小明在第二个路口遇到红灯的概率为_______.
4
π
13.已知α,β∈ 0, ,若P =sinαsin2β+cosαcosβ,则P的最大值为_______.
2
14.已知抛物线C:x2 =2py(p>0)的焦点为F ,直线l与抛物线C相切于点P(异于坐标原点O),与x轴
交于点Q,若 PF =2, FQ =1,则 p =_______;向量FP与PQ的夹角为_______.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
1
15.(13分)已知函数 f ( x )=ax+ .
ex
(1)讨论 f ( x )的单调性;
(2)若直线y =1与曲线y = f ( x )相切,求a的值.
π
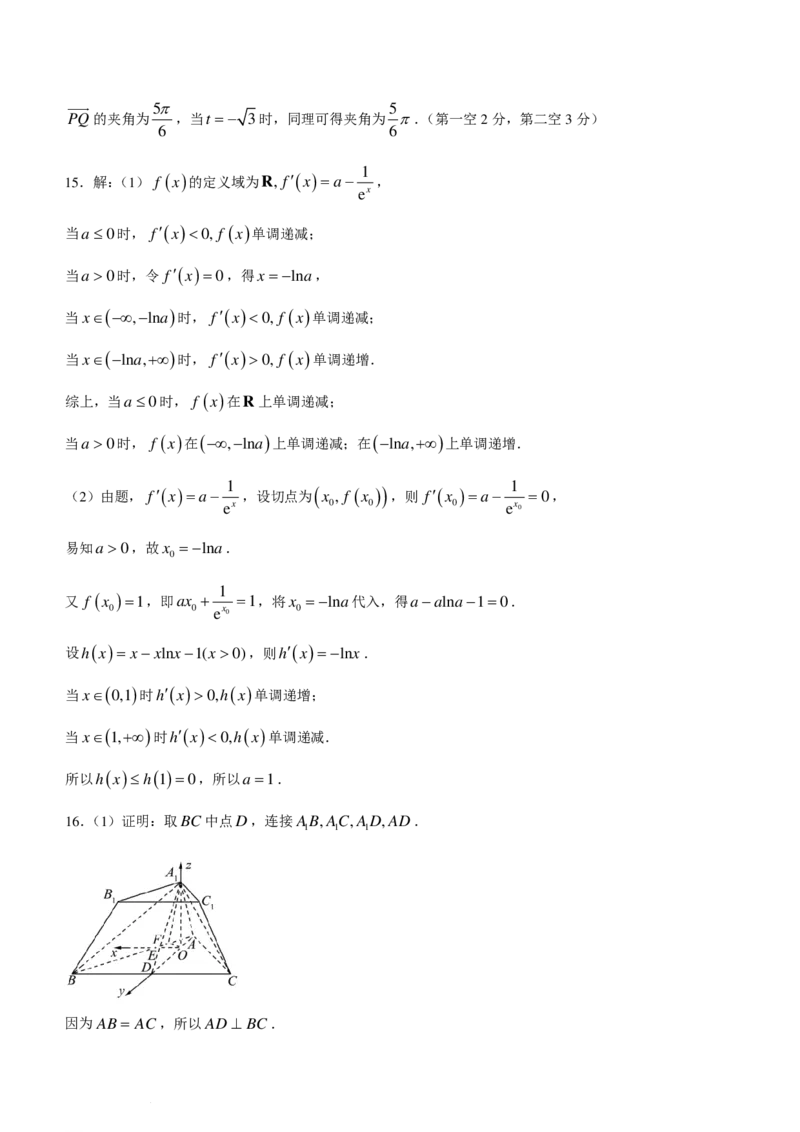
(15 分)如图,在三棱台ABC− ABC 中,AB = AC =2AB =2AA =4 2 ,∠AAB =∠AAC = ,
1 1 1 1 1 1 1 1 3
π
∠BAC = .
2
(1)证明:AA⊥ BC ;
1 1 1
(2)求直线BB 与平面AACC 所成角的正弦值.
1 1 1
17.(15分)某数学兴趣小组模拟“刮刮乐”彩票游戏,每张彩票的刮奖区印有从10个数字1,2,3,…,10
学科网(北京)股份有限公司中随机抽取的3个不同数字,刮开涂层即可兑奖,中奖规则为:若3个数的积为3的倍数且不为5的倍数时,
中三等奖;若3个数的积为5的倍数且不为3的倍数时,中二等奖;若3个数的积既为3的倍数,又为4的倍
数,且为7的倍数时,中一等奖;其他情况不中奖.
(1)随机抽取一张彩票,求这张彩票中奖的概率;
( )
(2)假设每张彩票售价为a a∈N* 元,且三、二、一等奖的奖金分别为5元,10元,50元,从出售该彩票
可获利的角度考虑,求a的最小值.
x2 y2
18.(17 分)已知椭圆C: + =1的右焦点为F,A为椭圆上一点,O为坐标原点,直线OA与椭圆交于
4 3
另一点B,直线AF 与椭圆交于另一点D(点B、D不重合).
3
(1)设直线AD,BD的斜率分别为k ,k ,证明:k ⋅k = − ;
AD BD AD BD 4
(2)点P为直线x =4上一点,记PA,PF,PD的斜率分别为k ,k ,k ,若k +2k +k =4,求点P的坐标.
1 2 3 1 2 3
19.(17分)在数列{ a }中,若存在常数t,使得a =aa a a +t ( n∈N* ) 恒成立,则称数列{ a }为“H ( t )
n n+1 1 2 3 n n
数列”.
1
(1)若c =1+ ,试判断数列{ c }是否为“H ( t )数列”,请说明理由;
n n n
n
(2)若数列{ a }为“H ( t )数列”,且a =2,数列{ b }为等比数列,且∑a2 =a +log b −t,求数列
n 1 n i n+1 2 n
i=1
{
b
}的通项公式;
n
(3)若正项数列{ a }为“H ( t )数列”,且a >1,t >0,证明:lna 0,所以复数z在复平面内对应的点在第三象限.故选
2i 2
C.
3.D 【解析】全称量词命题的否定为存在量词命题,所以“ ∀x< −1,log x2 >0 ”的否定为
2
“∃x<−1,log x2 ≤0”.故选D.
2
c
4.A 【解析】设双曲线的焦距为2c,由题,a =1,e= = 3,得c = 3,故b2 =c2 −a2 =2,所以
a
( )
2× − 3
( )
F − 3,0 ,不妨取渐近线y = 2x,则左焦点F 到渐近线 y = 2x的距离为 = 2 .故选A.
2+1
5.D 【解析】由题可得圆台的母线长为3 2,所以高h = (3 2)2 −(2 2 − 2)2 =4,所以该圆台的体
1 ( ) 56π
积V = ×4× 2π+8π+ 2π×8π = ,故选D.
3 3
6.D 【解析】因为1>m>n>0,所以lnm>lnn,又 y =nx为减函数,所以nlnm a =b,故选D.
1 1 3
7.A 【解析】S = ×AD×AC×sin∠DAC = ×4×AC× =4 3,解得AC =4,所以△ADC
△ADC
2 2 2
π 5π AB BD
为等腰三角形,∠ADC = ,故∠ADB = ⋅△ABD 中,由正弦定理得 = ,即
6 6 sin∠ADB sin∠BAD
2BD BD 1 5π 15
= ,得sin∠BAD = .因为∠ADB = ,所以∠BAD为锐角,故cos∠BAD = ,故
1 sin∠BAD 4 6 4
2
π 1 3 15− 3
sin∠ABD =sin (∠ADC−∠BAD )=sin −∠BAD = cos∠BAD− sin∠BAD = .故选A.
6 2 2 8
学科网(北京)股份有限公司m ( a +a ) n ( a +a ) m ( m−1 )
8.B 【解析】由题, 1 m =n2 = S , 1 n =m2 = S ,所以am+ d =n2①,
2 m 2 n 1 2
n ( n−1 ) m2 −n2 −m+n
an+ d =m2 ② , 两 式 作 差 得 a ( m−n )+ d =n2 −m2 , 化 简 得
1 2 1 2
m+n−1 ( m+n )( m+n−1 )
a + d = −( m+n ),即a ( m+n )+ d = −(m+n)2,所以S =−(m+n)2,故
1 2 1 2 m+n
选B.
9.BC 【解析】P(X =2)=C2(0.2)2 =0.04,A错误;若经验回归方程 y =b x+a 中斜率b >0,则变量x
2
1 1 1
与 y正相关,B正确;易得正态曲线关于直线x =0对称,故P(x >0)= ,又P ξ> = P ξ< − = p,
2 2 2
1 1
所以P0<ξ< = − p,C正确;掷一枚骰子,设事件A:出现的点数为1,事件B:出现的点数为2,则
2 2
A与B互斥,但A与B不互斥,D错误.故选BC.
x+π x
10.BC 【解析】 f ( x+π)=2sin ( x+π) cos2 = −2sinxsin2 ≠ f ( x ),A 错误;令 f ( x )=0,
2 2
x π 3π π 3π
得sinx =0或cos =0,当x∈ − , 时,解得x =0或x =π,故 f ( x )在 − , 上有 2 个零点,
2 2 2 2 2
x
B正确; f ( x )=2sinxcos2 =sinx+sinxcosx, f′( x )=2cos2x+cosx−1,令 f′( x )=0,得cosx = −1或
2
1 π π
cosx = ,且当x∈ −π,− 时,f′( x )<0, f ( x )单调递减,当x∈ − ,0时,f′( x )>0, f ( x )单调递
2 3 3
π π 3 3
增,所以 f ( x )在x = − 处取得极小值,C正确;可知 f ( x )的极大值为 f 2kπ+ = ,k∈Z,这个
3 3 4
π 3 3
极大值即为函数的最大值,f ( x )的极小值为 f 2kπ− = − ,k∈Z,这个极小值即为函数的最小值,
3 4
3 3
故∀x ,x ∈R, f ( x )− f ( x ) ≤ ,D错误.故选BC.
1 2 2 1 2
11.ACD 【解析】因为 f ( 2x+2 )为奇函数,所以 f (−2x+2 )= −f ( 2x+2 ),所以 f (−x+2 )=−f ( x+2 ),
学科网(北京)股份有限公司 1 3
故 f ( x+2 ) 为 奇 函 数 ,A 正 确 ; 又 f x+ = f −x , 故 f ( x+1 )= f ( 1−x ) , 所 以
2 2
f ( x )= f ( 2−x )= −f ( x+2 ) ,故 f ( x+4 )= f ( x ) ,所以 f ( x ) 是以 4 为周期的周期函数,所以
7 1 1 1
f = f − ,且不能确定 f = f − 一定成立,故 B 错误;因为 f ( x+1 )= f ( 1−x ),所以
2 2 2 2
1 3
f′( x+1 )= −f′( 1−x ) , 所 以 f′ = −f′ , C 正 确;因 为 f (−x+2 )=−f ( x+2 ) , 所 以
2 2
f′(−x+2 )= f′( x+2 ),故 f′(−x )= f′( x+4 ),又 f′( x )= f′( x+4 ),所以 f′(−x )= f′( x ),所以 f′( x )
为偶函数,D正确,故选ACD.
1
12. 【解析】记“小明在第一个路口遇到红灯”为事件A,“小明在第二个路口遇到红灯”为事件B,
4
则 P ( B A ) = 3 ,P ( B A ) = 1 ,又 P ( A ) = 3 ,P ( A )= 1 ,所以 P ( B )= P ( A ) P ( B A ) + P ( A ) P ( B A ) =
4 4 4 4
1 1 3 1 1
× + × = .
4 4 4 4 4
5 cosβ 1
13. 【解析】P = sin22β+cos2βsin (α+ϕ),其中tanϕ= = ,所以sin (α+ϕ)的最大
4 sin2β 2sinβ
5 5
值为1,设t = sin22β+cos2β= −4cos4β+5cos2β,当cos2β= 时,t取得最大值 ,所以P的最大
8 4
5
值为 .
4
5π p t2 x2 x
14.1; 【解析】由题得F0, ,设Pt, ,由x2 =2py得 y = ,求导得y′= ,所以直线
6 2 2p 2p p
t t2 t t
l 的 斜 率 k = , 则 直 线 l 的 方 程 为 y− = ( x−t ) , 易 得 Q ,0 , 所 以
p 2p p 2
t2 p t2 p2
PF = + =2, FQ = + =1 , 解 得 p =1,t = ± 3 . 当 t = 3 时 ,
2p 2 4 4
( ) 3 3 FP⋅PQ 3
FP = 3,1 ,PQ =− ,− ,则cos FP,PQ = = − FP,PQ ∈[ 0,π],故向量FP与
2 2 FP PQ 2
学科网(北京)股份有限公司
5π 5
PQ的夹角为 ,当t =− 3时,同理可得夹角为 π.(第一空2分,第二空3分)
6 6
1
15.解:(1) f ( x )的定义域为R, f′( x )=a− ,
ex
当a ≤0时, f′( x )<0, f ( x )单调递减;
当a >0时,令 f′( x )=0,得x = −lna,
当x∈(−∞,−lna )时, f′(
x
)<0,
f
(
x
)单调递减;
当x∈(−lna,+∞)时, f′(
x
)>0,
f
(
x
)单调递增.
综上,当a ≤0时, f ( x )在R上单调递减;
当a >0时, f ( x )在(−∞,−lna )上单调递减;在(−lna,+∞)上单调递增.
1 1
(2)由题, f′( x )=a− ,设切点为 ( x , f ( x )) ,则 f′( x )=a− =0,
ex 0 0 0 ex
0
易知a >0,故x = −lna.
0
1
又 f ( x )=1,即ax + =1,将x = −lna代入,得a−alna−1=0.
0 0 ex
0
0
设h ( x )= x−xlnx−1(x >0),则h′( x )= −lnx.
当x∈(
0,1
)时h′(
x
)>0,h (
x
)单调递增;
当x∈( 1,+∞)时h′(
x
)<0,h (
x
)单调递减.
所以h ( x )≤h ( 1 )=0,所以a =1.
16.(1)证明:取BC中点D,连接AB,AC,AD,AD.
1 1 1
因为AB = AC,所以AD ⊥ BC.
学科网(北京)股份有限公司π
因为∠AAB =∠AAC = ,AB = AC,且AA是公共边,所以△AAB≌△AAC ( SAS ),
1 1 3 1 1 1
所以AB = AC ,
1 1
所以AD ⊥ BC.
1
因为AD AD = D,AD,AD⊂平面AAD,所以BC ⊥平面AAD.
1 1 1 1
又因为AA⊂平面AAD,
1 1
所以AA⊥ BC.
1
又BC∥BC ,
1 1
所以AA⊥ BC
1 1 1
(2)解:如图,过点A 作AD的垂线,垂足为O,过点O作OF 垂直于AB,垂足为F ,连接AF .不难
1 1
得出, AB ⊥ AO,OF AO =O ,则 AB ⊥ 平面 AOF .又 AF ⊂ 平面 AOF ,则 AB ⊥ AF .由
1 1 1 1 1 1
π π
∠AAF = ,∠BAC = ,可得AF =OF = 2,AO = AO =2,OD =2,BD =4.
1 3 2 1
过点O作BC的平行线,交AB于点E,由(1)得OE,OD,OA 三条直线两两垂直,分别以OE,OD,OA 为
1 1
x , y,z 轴 建 立 空 间 直 角 坐 标 系 , 则 A ( 0,−2,0 ) ,C (−4,2,0 ) ,A ( 0,0,2 ) ,B ( 4,2,0 ) ,B ( 2,2,2 ) ,
1 1
AA =( 0,2,2 ) ,AC =(−4,4,0 ) ,BB = BA+ AA + AB =(−2,0,2 ).
1 1 1 1 1
设平面AACC 的一个法向量为m =( x,y,z ),
1 1
m⋅AA =0, 2y+2z =0,
则 1 即
m⋅AC =0, −4x+4y =0.
令x =1,得 y =1,z = −1,所以m =( 1,1,−1 ).
又直线BB 的一个方向向量n =(−2,0,2 ),
1
m⋅n −4 6
所以cos m,n = = = − ,
m ⋅ n 3×2 2 3
6
所以直线BB 与平面AACC 所成角的正弦值为 .
1 1 1 3
学科网(北京)股份有限公司( )
C3+C2C1 + C1C1 +1+C1C2
13
17.解:(1)获得三等奖的概率P = 3 3 5 2 2 3 4 = ;
3 C3 40
10
C1C2 +C2C1 5
获得二等奖的概率P = 2 5 2 5 = ;
2 C3 24
10
C1C1C1 +C1C1C1 1
获得一等奖的概率P = 1 2 2 1 1 4 = .
1 C3 15
10
79
所以随机抽取一张彩票,这张彩票中奖的概率P = P +P +P = .
1 2 3 120
(2)一张彩票的奖金ξ的取值可能为0,5,10,50元,其分布列为:
ξ 0 5 10 50
2 13 5 1
P
5 40 24 15
2 13 5 1 169
所以ξ的期望E (ξ)=0× +5× +10× +50× = .
5 40 24 15 24
169
若盈利,需a > E (ξ)= ,
24
因为a∈N*,故a的最小值为8.
18.(1)证明:设D ( x ,y ) ,A ( x ,y ),则B (−x ,−y ),
0 0 1 1 1 1
y − y y + y y2 − y2
则k ⋅k = 0 1 × 0 1 = 0 1 .
AD BD x −x x + x x2 −x2
0 1 0 1 0 1
x2 y2 x2 y2
又 1 + 1 =1, 0 + 0 =1,
4 3 4 3
x2 −x2 y2 − y2
两式作差得: 0 1 + 0 1 =0,
4 3
y2 − y2 3
即 0 1 = − ,
x2 −x2 4
0 1
3
所以k ⋅k = − ,得证.
AD BD 4
学科网(北京)股份有限公司(2)解:由题,A不与长轴两端点重合,设P ( 4,m ) ,m ≠0,直线AF :x =ty+1,
( )
与椭圆方程联立,并消去x得 3t2 +4 y2 +6ty−9=0.
−6t −9
设A ( x ,y ) ,D ( x ,y ),则 y + y = ,y y = ,
1 1 2 2 1 2 3t2 +4 1 2 3t2 +4
m−0 m
所以k = = ,
2 4−1 3
m− y m− y ( 4−x )( m− y )+( 4−x )( m− y )
k +k = 1 + 2 = 2 1 1 2 .
1 3 4−x 4−x ( 4−x )( 4−x )
1 2 1 2
又x =ty +1,x =ty +1,代入上式化简得
1 1 2 2
( 3+tm )×6t 18t
k +k =
6m−( 3+tm )( y
1
+ y
2
)+2ty
1
y
2 =
6m+
3t2 +4
−
3t2 +4
=
2mt2 +2m
=
2m
,
1 3 9−3t ( y + y )+t2y y 18t2 9t2 3t2 +3 3
1 2 1 2 9+ −
3t2 +4 3t2 +4
4m
所以k +2k +k = =4.故m =3,
1 2 3 3
所以点P的坐标为(
4,3
).
19.(1)解:数列{
c
}不是“H (
t
)数列”.
n
理由如下:
1 n+1 n+2
因为c =1+ = ,所以c = .
n n n n+1 n+1
2 3 4 n+1
又cc c = × × ×× =n+1,
1 2 n 1 2 3 n
n+2 1
所以c −cc c = −( n+1 )= −n,
n+1 1 2 n n+1 n+1
1
因为 −n不是常数,所以数列{ c }不是“H ( t )数列”.
n+1 n
n n
(2)解:因为数列{ a }为“H ( t )数列”,由∑a2 =a +log b −t,得∑a2 =aa a +log b ,
n i n+1 2 n i 1 2 n 2 n
i=1 i=1
学科网(北京)股份有限公司n+1 b
所以∑a2 =aa a a +log b ,两式作差得:a2 =( a −1 ) aa a +log n+1 .
i 1 2 n n+1 2 n+1 n+1 n+1 1 2 n 2 b
i=1 n
又数列{ a }为“H ( t )数列”,故a −t =aa a .
n n+1 1 2 n
设数列{
b
}的公比为q,
n
所以a2 =( a −1 )( a −t )+log q,
n+1 n+1 n+1 2
即( t+1 ) a −( t+log q )=0对∀n∈N*成立,
n+1 2
t+1=0,
则 得t = −1,q=2.
t+log q=0,
2
又a =2,a2 =a +log b ,得b =4,
1 1 1 2 1 1
所以b =4×2n−1 =2n+1,
n
所以数列{ b }的通项公式为b =2n+1.
n n
1 1−x
(3)证明:设函数 f ( x )=lnx−x+1,则 f′( x )= −1= ,
x x
当x∈( 1,+∞)时, f′(
x
)<0,则
f
(
x
)在( 1,+∞)上单调递减,且
f
(
x
)<
f
(
1
)=0.
因为数列{ a }为“H ( t )数列”,则a −aa a =t ( n∈N* ) .
n n+1 1 2 n
因为a >1,t >0,则a =a +t >a >1,故a =aa +t >aa >1,
1 2 1 1 3 1 2 1 2
以此类推,可得对∀n∈N*,a >1,
n
所以 f ( a )< f ( 1 )=0,即lna −a +1<0,
n n n
所以lna