文档内容
决胜新高考——2024 届高三年级大联考
数学
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只
有一个是符合题目要求的,请把答案填涂在答题卡相应位置上)
1.已知集合 ,则下列关系一定正确的是( )
A. B. C. D.
2.已知数列 是公差为 的等差数列,对正整数 ,若 ,则 ,是
的( )
A.充分不必要条件 B.必要不充分条件
C.既不充分也不必要条件 D.充要条件
3.已知复数 满足 (其中 为虚数单位),且 的虚部为 ,则 ( )
A. B. C. D.
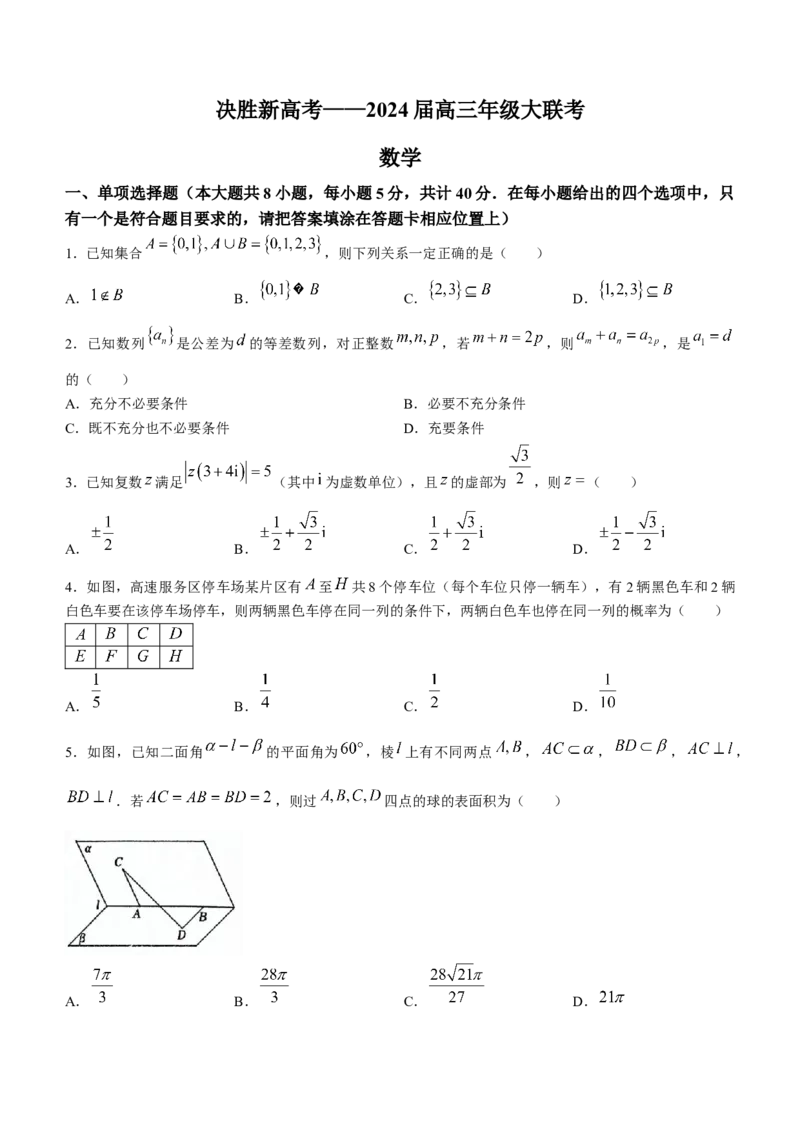
4.如图,高速服务区停车场某片区有 至 共8个停车位(每个车位只停一辆车),有2辆黑色车和2辆
白色车要在该停车场停车,则两辆黑色车停在同一列的条件下,两辆白色车也停在同一列的概率为( )
A. B. C. D.
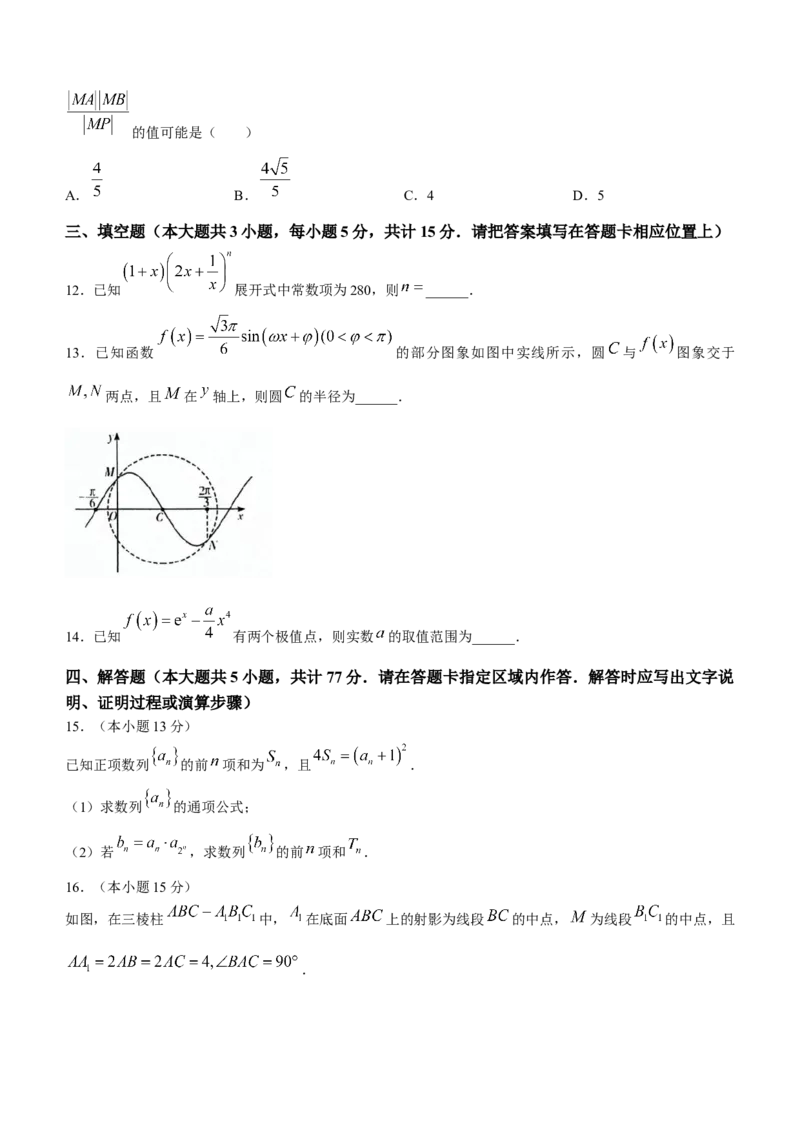
5.如图,已知二面角 的平面角为 ,棱 上有不同两点 , , , ,
.若 ,则过 四点的球的表面积为( )
A. B. C. D.
学科网(北京)股份有限公司6.已知 ,则 ( )
A. B. C. D.
7.已知 为椭圆 与双曲线 公共的焦点,且 在第一象限内的交点为P,若 的离心率
满足 ,则 ( )
A. B. C. D.
8.已知定义在 上的函数 ,对任意正数x,y满足 ,且当 时,
,若 ,则实数a的取值范围是( )
A. B. C. D.
二、多项选择题(本大题共3小题,每小题6分,共计18分.在每小题给出的四个选项中,至
少有两个是符合题目要求的,请把答案填涂在答题卡相应位置上)
9.已知单位向量 的夹角为θ,则下列结论正确的有( )
A. B. 在 方向上的投影向量为
C.若 ,则 D.若 则
10.已知随机变量 服从正态分布 ,定义函数 为 取值不小于 的概率,即
,则( )
A. B.
C. 为减函数 D. 为偶函数
11.已知点 在曲线 上运动,过 作以 为圆心,1为半径的圆的两条切线 ,则
学科网(北京)股份有限公司的值可能是( )
A. B. C.4 D.5
三、填空题(本大题共3小题,每小题5分,共计15分.请把答案填写在答题卡相应位置上)
12.已知 展开式中常数项为280,则 ______.
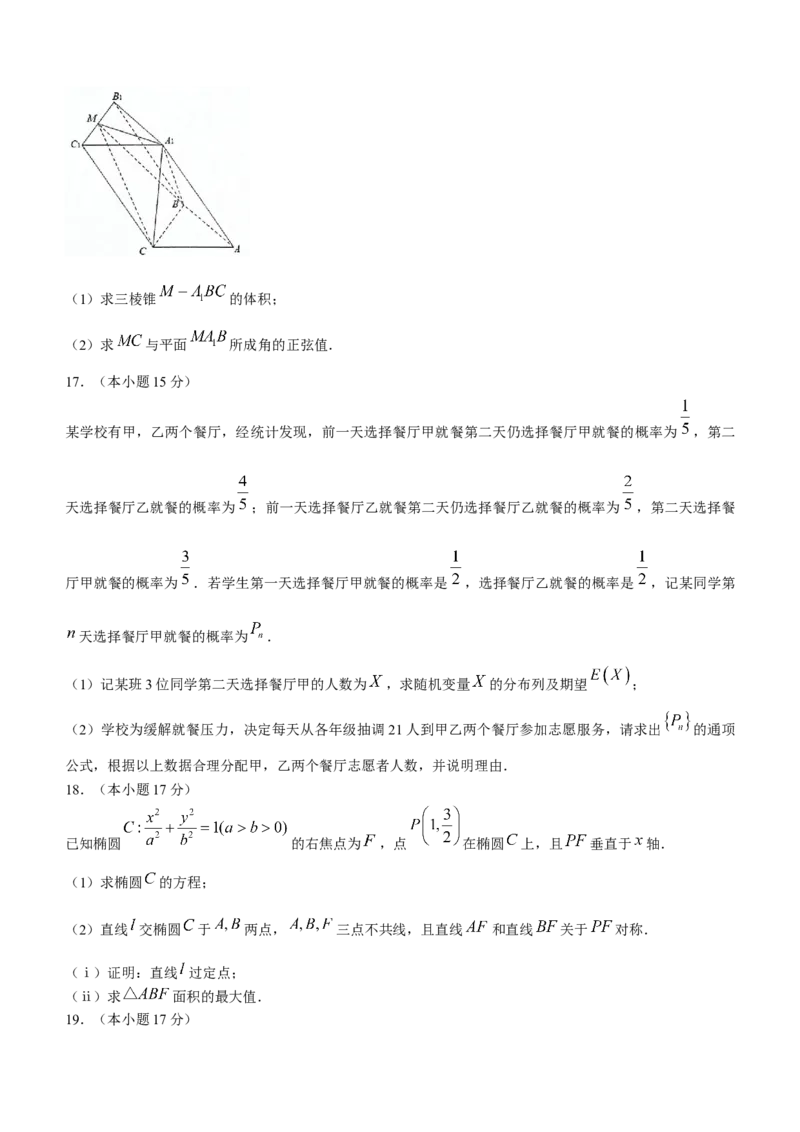
13.已知函数 的部分图象如图中实线所示,圆 与 图象交于
两点,且 在 轴上,则圆 的半径为______.
14.已知 有两个极值点,则实数 的取值范围为______.
四、解答题(本大题共5小题,共计77分.请在答题卡指定区域内作答.解答时应写出文字说
明、证明过程或演算步骤)
15.(本小题13分)
已知正项数列 的前 项和为 ,且 .
(1)求数列 的通项公式;
(2)若 ,求数列 的前 项和 .
16.(本小题15分)
如图,在三棱柱 中, 在底面 上的射影为线段 的中点, 为线段 的中点,且
.
学科网(北京)股份有限公司(1)求三棱锥 的体积;
(2)求 与平面 所成角的正弦值.
17.(本小题15分)
某学校有甲,乙两个餐厅,经统计发现,前一天选择餐厅甲就餐第二天仍选择餐厅甲就餐的概率为 ,第二
天选择餐厅乙就餐的概率为 ;前一天选择餐厅乙就餐第二天仍选择餐厅乙就餐的概率为 ,第二天选择餐
厅甲就餐的概率为 .若学生第一天选择餐厅甲就餐的概率是 ,选择餐厅乙就餐的概率是 ,记某同学第
天选择餐厅甲就餐的概率为 .
(1)记某班3位同学第二天选择餐厅甲的人数为 ,求随机变量 的分布列及期望 ;
(2)学校为缓解就餐压力,决定每天从各年级抽调21人到甲乙两个餐厅参加志愿服务,请求出 的通项
公式,根据以上数据合理分配甲,乙两个餐厅志愿者人数,并说明理由.
18.(本小题17分)
已知椭圆 的右焦点为 ,点 在椭圆 上,且 垂直于 轴.
(1)求椭圆 的方程;
(2)直线 交椭圆 于 两点, 三点不共线,且直线 和直线 关于 对称.
(ⅰ)证明:直线 过定点;
(ⅱ)求 面积的最大值.
19.(本小题17分)
学科网(北京)股份有限公司已知函数 ,其中 , 为自然对数的底数.
(1)函数 ,求 的最小值 ;
(2)若 为函数 的两个零点,证明: .
学科网(北京)股份有限公司