江苏省决胜新高考2024届高三下学期4月大联考数学试题（含答案）(1)_2024年4月_024月合集_2024届江苏省决胜新高考高三下学期4月大联考

决胜新高考——2024 届高三年级大联考 数 学 注 意 事 项 考生在答题前请认真阅读本注意事项及各题答题要求 1．本试卷共4页，包含［单选题（1~8）多选题9~12，填空题（第13题～第16题，共80分）、解 答题（第17～22题，共70分）。本次考试时间120分钟，满分150分、考试结束后，请将答题 卡交回。 2．答题前，请考生务必将自己的姓名、学校、班级、座位号、考试证号用0.5毫米的黑色签字笔写 在答题卡上相应的位置，并将考试证号用2B铅笔正确填涂在答题卡的相应位置。 3．答题时请用0.5毫米的黑色签字笔在答题卡指定区域作答。在试卷或草稿纸上作答一律无效。 4．如有作图需要，可用2B铅笔作图，并请加黑加粗，描写清楚。 一、单选题：本大题共8小题，每题5分，共40分。在每小题提供的四个选项中，只有一项是符合题目 要求的。 1. 已知向量a，b满足|a|＝1，|b|＝2 3， b·(2a－b)=18，则a与b的夹角等于 A．30 B．60 C．120 D．150 2. 若复数zcosisin，则 z22i 的最大值是 A．2 21 B．2 21 C． 21 D．2 2 3 3. 已知甲、乙两支篮球队各6名队员某场比赛的得分数据（单位：分）从小到大排列如下：甲队：7， 12，12，20，20x，31；乙队：8，9，10+y，19，25，28.这两组数据的中位数相等，且平均值也相 等，则xy的值为 A． 3 B．4 C．5 D．6 4. 已知x 2x1 4， x log x 4，则x x 的值为 1 2 2 2 1 2 A．2 B．3 C．4 D．5 π 5. 若3sin4cos5，则tan( ) 4 1 1 A．7 B．7 C． D． 7 7 6. 经过抛物线C：y2 4x焦点F 的直线与C交于A，B两点，与抛物线C的准线交于点P，若AF ， AP，BF 成等差数列，则AB 8 16 A．2 3 B．2 6 C． D． 3 3 高三数学 第1页（共4页） {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}7. 贝塞尔曲线(Beziercurve)是应用于二维图形应用程序的数学曲线，一般的矢量图形软件通过它来 精确画出曲线. 三次函数 f(x)的图象是可由A，B，C，D四点确定的贝塞尔曲线，其中A，D 在 f(x)的图象上，f(x)在点A，D处的切线分别过点B，C.若A(0，0)，B(1，1)，C(2，2)，D(1，0)， 则 f(x) A．5x3 4x2 x B．3x3 3x C．3x34x2x D．3x32x2x 8. 已知函数 f(x) x2 8x，且点P(x，y)满足 f(x) f(y)≤32，f(y)≤0，若记点P构成的图形 为，则的面积是 64π 64π A． 16 3 B． 16 3 C．6416 3 D．6416 3 3 3 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。 全部选对的得6分，部分选对的得部分分，有选错的得0分。 9. 若(x2 x2)10 a axa x2 a x3 a x20，则 0 1 2 3 20 A．a 1024 B．a 1 0 1 C．a 10 D．a a a a 512 19 1 3 5 19 10. 某企业使用新技术对某款芯片制造工艺进行改进.部分芯片由智能检测系统进行筛选，其中部分 次品芯片会被淘汰，筛选后的芯片及未经筛选的芯片进入流水线由工人进行抽样检验.记A表 示事件“某芯片通过智能检测系统筛选”，B表示事件“某芯片经人工抽检后合格”.改进生产工艺 后，该款芯片的某项质量指标服从正态分布N(5.40,0.052)，现从中随机抽取M 个，这M 个 芯片中恰有m个的质量指标位于区间(5.35,5.55)，则下列说法正确的是 （若 N(,2)，则P()0.6826,P(33)0.9974） A．P  B A PB B．P  A B P  AB  C．P5.355.550.84 D．Pm45取得最大值时，M 的估计值为53 11. 若正实数a，b满足12abab，则 A．b12 B．有序数对(a，b)(a，bN*)有6个 C．ab的最小值是124 3 D．a2 b2 2a24b1210 高三数学 第2页（共4页） {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}三、填空题：本大题共3小题，每小题5分，共15分．不需写出解答过程，请把答案直接填写在答题卡 相应位置上． 1 12. 将函数 f(x)sin(2x)图象上的每个点的横坐标变为原来的 倍（纵坐标不变），再将得到的 2 π 图象向左平移 个单位长度，所得的图象关于y 轴对称，写出一个符合条件的的值 ▲ 6 13. 已知定义在R上的 f x满足 f( 1 )0，且 f(x y) f(x)f(y)4xy ，则 f(0) ▲ 2 14. 已知一个顶点为P，底面中心为O的圆锥的体积为9π，该圆锥的顶点P和底面圆周均在球O 上. 1 若圆锥的高为3，则球O 的半径为 ▲ ；球O 的体积的最小值是 ▲ . 1 1 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程戓演算步骤。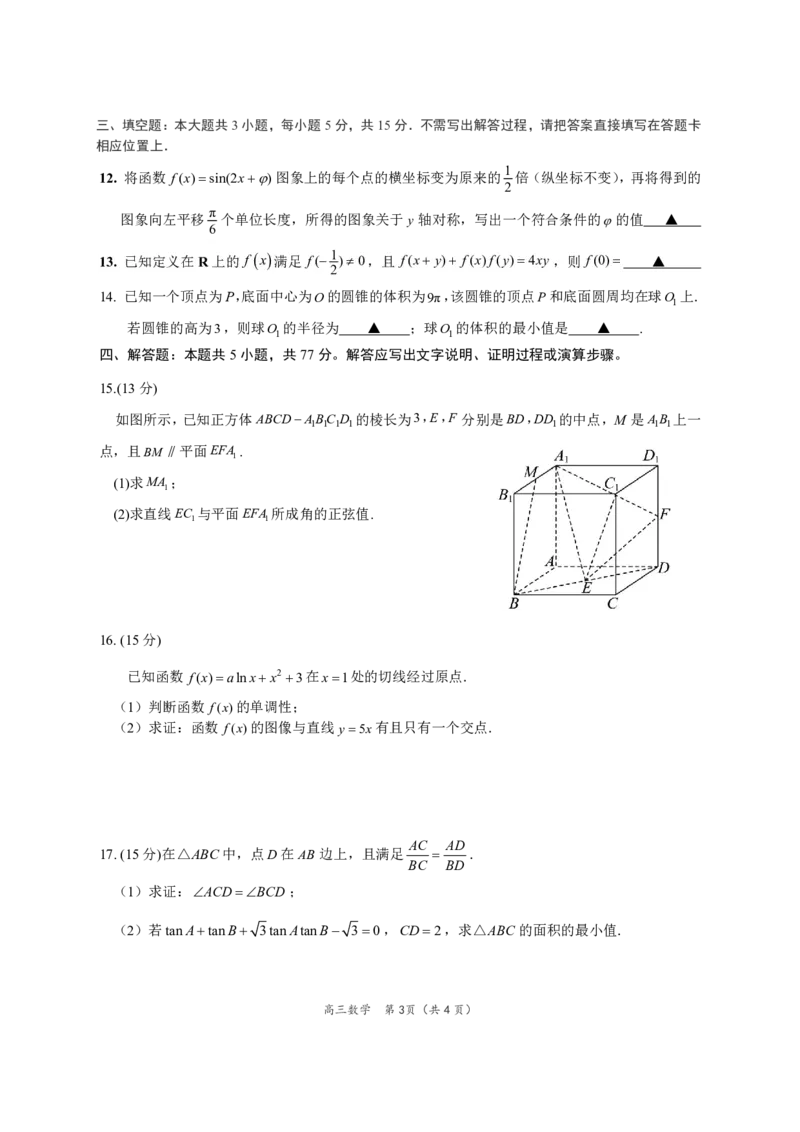 15.(13分) 如图所示，已知正方体ABCDABC D 的棱长为3，E，F 分别是BD，DD 的中点，M 是AB 上一 1 1 1 1 1 1 1 点，且BM 平面EFA . 1 (1)求MA ； 1 (2)求直线EC 与平面EFA 所成角的正弦值. 1 1 16.(15分) 已知函数 f(x)alnxx2 3在x1处的切线经过原点. （1）判断函数 f(x)的单调性； （2）求证：函数 f(x)的图像与直线y5x有且只有一个交点. AC AD 17.(15分)在△ABC中，点D在AB 边上，且满足  . BC BD （1）求证：ACDBCD ； （2）若tanAtanB 3tanAtanB 30，CD2，求△ABC的面积的最小值. 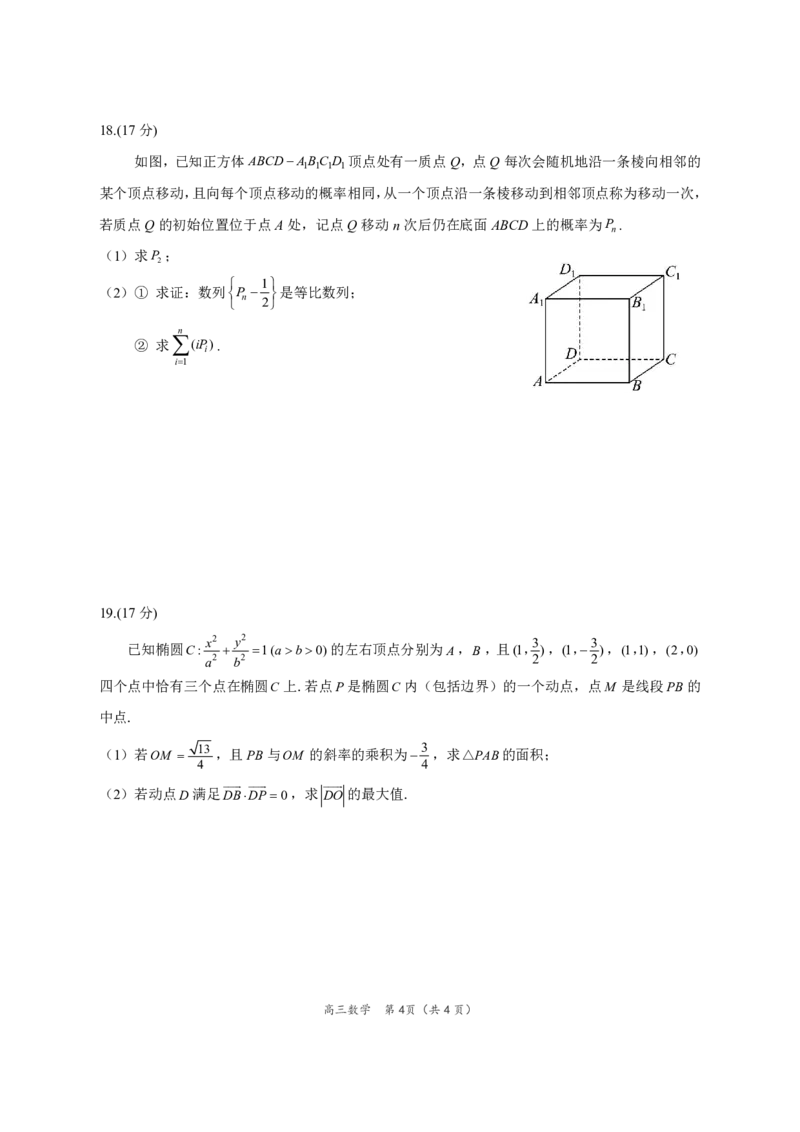高三数学 第3页（共4页） {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}18.(17分) 如图，已知正方体ABCDABC D 顶点处有一质点Q，点Q每次会随机地沿一条棱向相邻的 1 1 1 1 某个顶点移动，且向每个顶点移动的概率相同，从一个顶点沿一条棱移动到相邻顶点称为移动一次， 若质点Q的初始位置位于点A处，记点Q移动n次后仍在底面ABCD上的概率为P . n （1）求P ； 2  1 （2）① 求证：数列P  是等比数列； n  2 n ② 求 (iP). i i1 19.(17分) x2 y2 3 3 已知椭圆C:  1(ab0)的左右顶点分别为A，B，且(1，)，(1， )，(1，1)，(2，0) a2 b2 2 2 四个点中恰有三个点在椭圆C 上.若点P是椭圆C内（包括边界）的一个动点，点M 是线段PB的 中点. （1）若OM  13 ，且PB与OM 的斜率的乘积为 3 ，求△PAB的面积； 4 4    （2）若动点D满足DBDP0，求 DO 的最大值. 高三数学 第4页（共4页） {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}决胜新高考——2024 届高三年级大联考 数学参考答案与评分标准 一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有 一项是符合题目要求的． 1. D 2. B 3.A 4.C 5. B 6. D 7.C 8. A 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要 求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 9. ACD 10. ACD 11.AB 三、填空题：本题共3小题，每小题5分，共15分．  12. k ,kZ 13 6 试卷第1页，共7页  1 14. 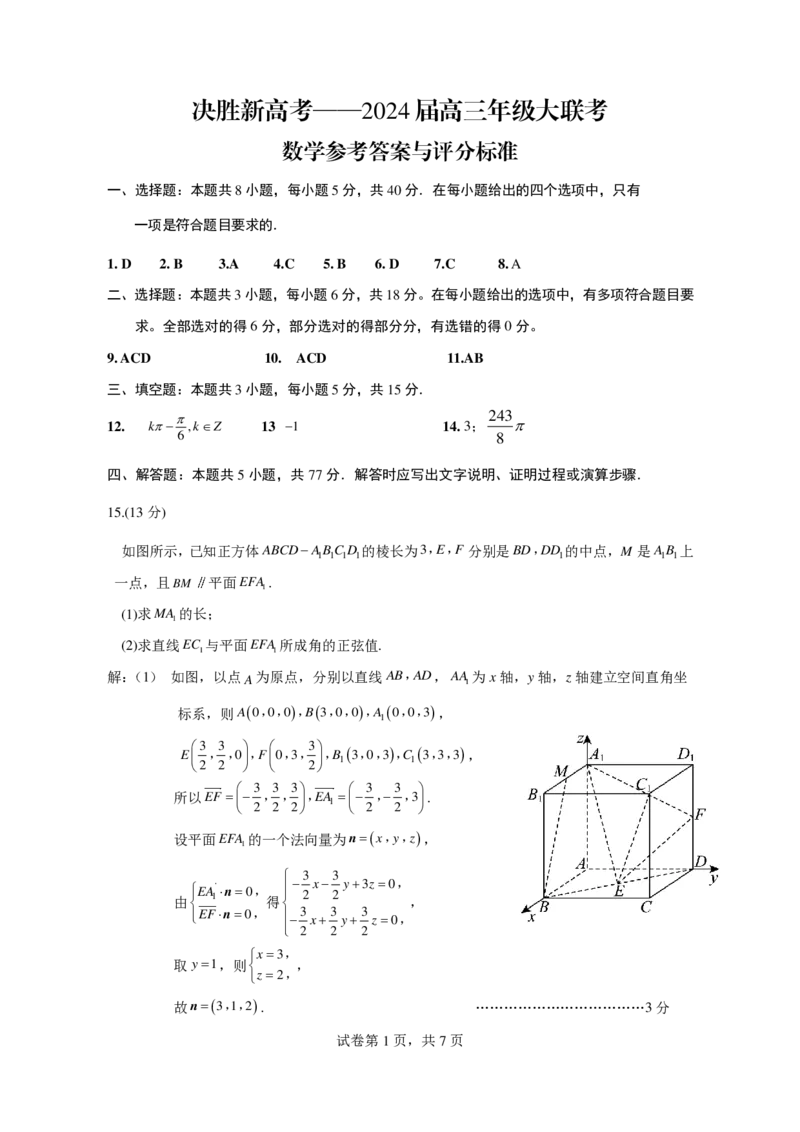3； 2 4 8 3  四、解答题：本题共5小题，共77分．解答时应写出文字说明、证明过程或演算步骤． 15.(13分) 如图所示，已知正方体ABCDABCD 的棱长为 1 1 1 1 3 ， E ， F 分别是BD，DD 的中点， 1 M 是 A 1 B 1 上 一点，且 B M 平面 E F A 1 . (1)求MA 的长； 1 (2)求直线EC 与平面EFA 所成角的正弦值. 1 1 解：（1） 如图，以点 A 为原点，分别以直线 A B ， A D ， A A 1 为x轴，y轴，z轴建立空间直角坐 标系，则A0，0，0，B3，0，0，A 0，0，3， 1 E  3 2 ， 3 2 ， 0  ， F  0 ， 3 ， 3 2  ， B 1  3 ， 0 ， 3  ， C 1  3 ， 3 ， 3  ， 所以 E F    3 2 ， 3 2 ， 3 2  ， E A 1    3 2 ，  3 2 ， 3  . 设平面 E F A 1 的一个法向量为 n   x ， y ， z  ，  3 3  x y3z0， 由    EA 1 n0， 得    2 2 ， EFn0，  3 x 3 y 3 z0，  2 2 2 x3， 取y1，则 ， z2， 故n3，1，2. ………………………………3分 {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}设 试卷第2页，共7页 M  t ， 0 ， 3  ，则 B M   t  3 ， 0 ， 3  . 因为 B M 平面 E F A 1 ，所以 n  B M  3 ( t  3 )  2  3  0 ， 所以t 1，所以 M A 1  1 . ………………………………7分 （2）因为 E C 1   3 2 ， 3 2 ， 3  ， ………………………………9分 平面 E F A 1 的一个法向量为 n   3 ， 1 ， 2  ， 设直线 E C 1 与平面 E F A 1 所成角为， 故 s in c o s E C 1 E E C C 1 1 9 4 3 2 , 9 4 3 2 , 3 9  3 ,1 9 , 2 1  4 4 2 2 1 1    ， n     n n           ， 所以直线 E C 1 与平面 E F A 1 4 21 所成角的正弦值为 .………………………………13分 21 16（15分） 已知函数 f ( x )  a ln x  x 2  3 在 x  1 处的切线经过原点. （1）判断函数 f ( x ) 的单调性； （2）求证：函数 f(x)的图像与直线y5x有且只有一个交点. 解：（1）因为 f (1 )  a ln 1  1  3  4 ，所以切点为 (1 ， 4 ) . a 因为 f(x) 2x，所以 x f (1 )  a  2 ， 所以切线方程为y4(a2)(x1). ………………………………3分 因为切线经过原点，所以 0  4  ( a  2 ) ( 0  1 ) ，所以 a  2 . 故 f ( x )  2x  2 x  0 ， 所以 f(x)在(0，)上单调递增. ………………………………6分 （2）设g(x) f(x)5x2lnxx235x(x0)， 则 g ( x )  2 x 2  5x x  2  ( 2 x  1 )x ( x  2 ) . ………………………………8分 1 因为当x(0，)时，g(x)0，g(x)单调递增， 2 1 当x( ，2)时，g(x)0， 2 g ( x ) 单调递减， e3 ln 且g( 1 )2ln 1 ( 1 )23 5 2ln2 3  38ln2  256 0， 2 2 2 2 4 4 4 {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}因为 试卷第3页，共7页 g ( 12 )  0 ，且当 x  ( 12 ， 2 ) 时， g ( x ) 单调递减，所以 g ( 2 )  g ( 12 )  0 所以当 x  ( 0 ， 2 ) 时， g ( x )  0 ， 所以函数 g ( x ) 在 x  ( 0 ， 2 ) 时没有零点， 所以当x(0，2)时，函数 f(x)的图像与直线y5x没有交点.…………………11分 当 x  ( 2 ，   ) 时， g ( x )  0 ， g ( x ) 单调递增， 又因为 g ( 5 )  2 ln 5  3  0 ，且函数 g ( x ) 的图像是不间断的， 所以当 x  ( 2 ，   ) 时，函数 g ( x ) 有且只有一个零点， 函数 f ( x ) 的图像与直线 y  5 x 有且只有一个交点. 综上所述，函数 f(x)的图像与直线 y  5 x 有且只有一个交点.…………………15分 17.(15分) 在 △ A B C 中，点 D 在 A B 边上，且满足 A B C C  A B D D . （1）求  A C D   B C D ； （2）若 ta n A  ta n B  3 ta n A ta n B  3  0 ， C D  2 ，求 △ A B C 的面积的最小值. 解：（1）在 △ A C D AC AD 中，由正弦定理  ，得 sinADC sinACD A A C D  s s in in   A A D C C D . BC BD BC sinBDC 在△BCD中，由正弦定理  ，得  . sinBDC sinBCD BD sinBCD 因为 A B C C  A B D D ，所以 A A C D  B B C D sinADC sinBDC ，所以  . ……………3分 sinACD sinBCD 因为ADCBDC π，所以ADC πBDC， 所以 s in  A D C  s in ( π   B D C )  s in  B D C ， 所以 s i n  A C D  s i n  B C D . 又因为ACD，BCD(0，π)，且ACDBCDπ， 所以  A C D   B C D . ………………………………7分 （2）因为 ta n A  ta n B  3 ta n A ta n B  3  0 ， 所以 ta n A  ta n B  3 (1  ta n A ta n B ) ， tanAtanB 所以tan(AB)  3， ………………………………9分 1tanAtanB 因为0 ABπ，所以 A  B  π 3 ，所以 c  π  ( A  B )  2 π 3 ． 因为S S S ， △ABC △ACD △BCD {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}所以 试卷第4页，共7页 1 2  A C  B C  s in 2 π 3  1 2  A C  C D  s in π 3  1 2  B C  C D  s in π 3 ， 所以 A C  B C  2 A C  2 B C  2 ( A C  B C ) ． ………………………………12分 因为 A C  B C ≥ 2 A C  B C ， 所以 A C  B C  2 A C  2 B C  2 ( A C  B C ) ≥ 4 A C  B C ， 所以 A C  B C ≥ 1 6 ，当且仅当 A C  B C = 4 时等号成立． 所以 △ A B C 的面积的最小值为 1 2  1 6  2 3  4 3 . 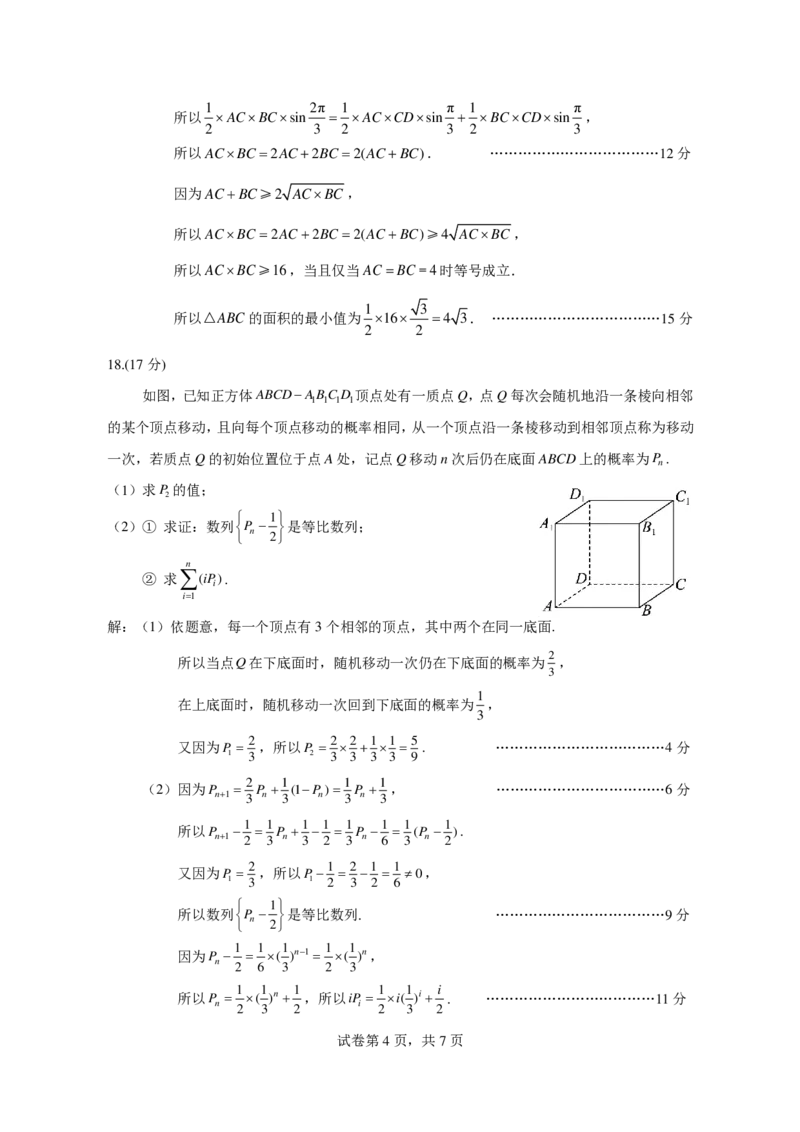………………………………15分 18.(17分) 如图，已知正方体 A B C D  A 1 B 1 C 1 D 1 顶点处有一质点Q，点Q每次会随机地沿一条棱向相邻 的某个顶点移动，且向每个顶点移动的概率相同，从一个顶点沿一条棱移动到相邻顶点称为移动 一次，若质点Q的初始位置位于点A处，记点Q移动n次后仍在底面ABCD上的概率为 P n . （1）求 P 2 的值； （2）① 求证：数列  P n  1 2  是等比数列； ② 求 n i 1 ( iP i ) . 解：（1）依题意，每一个顶点有3个相邻的顶点，其中两个在同一底面. 2 所以当点Q在下底面时，随机移动一次仍在下底面的概率为 ， 3 在上底面时，随机移动一次回到下底面的概率为 1 3 ， 2 又因为P  ，所以 1 3 P 2  23  23  13  13  59 . ………………………………4分 2 1 1 1 （2）因为P  P  (1P ) P  ， ………………………………6分 n1 3 n 3 n 3 n 3 所以 P n  1  12  13 P n  13  12  13 P n  16  13 ( P n  12 ) . 2 1 2 1 1 又因为P  ，所以P     0， 1 3 1 2 3 2 6 所以数列  P n  1 2  是等比数列. ………………………………9分 因为 P n  1 2  1 6  ( 1 3 ) n  1  1 2  ( 1 3 ) n ， 1 1 1 1 1 i 所以P  ( )n ，所以iP  i( )i  . ………………………………11分 n 2 3 2 i 2 3 2 {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}设 试卷第5页，共7页 a i  i ( 1 3 ) i ， 则 n i 1 ( ia i )  1  ( 1 3 1)  2  ( 1 3 ) 2  3  ( 1 3 ) 3   n  ( 1 3 ) n ， n 1 1 1 1 1 则  (ia )1( )22( )33( )4 n( )n1， 3 i 3 3 3 3 i1 所以 2 3 n i 1 ( ia i )  1  ( 1 3 1)  1  ( 1 3 ) 2  1  ( 1 3 ) 3  1  ( 1 3 ) 4   1  ( 1 3 ) n  n  ( 1 3 ) n  1 ， 所以 2 3 n i 1 ( ia i )  1 3  1  1 (  1 31 3 ) n  n  ( 1 3 ) n  1  1 2  1 2  ( 1 3 ) n  n  ( 1 3 ) n  1 ， 所以 n i 1 ( ia i )  3 4  ( 3  4 2 n )  ( 1 3 ) n . 1 n 又因为 n i 2  2 n2n，  n 2 2 4 i1 所以 n i 1 ( iP i )  3 8  ( 3  8 2 n )  ( 1 3 ) n  n 2  4 n . ………………………………17分 19.(17分) 已知椭圆 C : x a 2 2  y b 2 2  1 ( a  b  0 ) 的左右顶点分别为 A ， B ，且 (1 ， 32 ) ， (1 ，  32 ) ， (1 ， 1 ) ，(2，0) 四个点中恰有三个点在椭圆 C 上.若点 P 是椭圆 C 内（包括边界）的一个动点，点 M 是线段 P B 的中点. （1）若 O M  14 3 ，且 P B 与 O M 3 的斜率的乘积为 ，求 4 △ P A B 的面积； （2）若动点D满足 D B  D P  0 ，求 D O 的最大值. 3 3 解：因为(1，)与(1， )关于x轴对称，所以这两个点必定都在椭圆C上， 2 2 1 9 所以  1. ………………………………2分 a2 4b2 若点 (1 ， 1 ) 在椭圆 C 1 1 上，则  1. a2 b2  1 9  1，  a2 4b2 因为方程组  无解，所以点(1，1)不在椭圆C上. 1 1   1 a2 b2 {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}若点 试卷第6页，共7页 ( 2 ， 0 ) 在椭圆 C 上，则 42 a  1 ，所以 a  2 ， b  3 . 综上可知：椭圆 C : 2 x4  y3 2  1 . ………………………………4分 （1）因为点 M 是线段 P B 的中点，点 O 是线段 A B 的中点， 所以 M O //A P ， M O  12 A P ， 13 3 所以AP2MO ，k k  . 2 AP BP 4 设 P ( x 0 ， y 0 ) ，则 A P 2  ( x 0  2 ) 2  y 0 2  1 34 ， k A P k B P  x y 0 0 2  x y 0 0 2   34 . ………………………………6分 化简得 x 0 2  1 6 x 0  1 5  0 ，所以 x 0   1 或 x 0   1 5 ， 又因为点 P 是椭圆 C 内（包括边界）的一个动点，所以 x 0   1 . 因为 x y 0 0 2  x y 0 0 2   34 ，所以 y 0 2  94 3 ，所以 y  . 0 2 所以 △ P A B 的面积为 12  4  32  3 . ………………………………8分 （2）因为动点 D 满足DBDP0，所以点 D 在以 P B 为直径的圆上. 因为点M 是线段PB的中点，所以OD≤OM MD. 因为 O M  12 A P ， D M  12 P B 1 1 1 ，所以OD≤ AP PB (APPB). 2 2 2 设APPB2m，则当 m  2 时，点 P 在线段 A B 上，此时 O D ≤ 2 .………………10分 当 m  2 时，设 P ( x ， y ) ，点 P 在以 A ， B 为焦点的椭圆 x m 2 2  m y2 2  4  1 上. 若 m  7 ，则 2 x4  y3 2  ( x m 2 2  m y2 2  4 )  ( m 2  m 42 ) x 2  ( m 3 ( 2 m 2 7  ) y 4 2 )  0 ， 所以 2 x4  y3 2  x m 2 2  m y2 2  4  1 ，所以点 P 在椭圆 C 外，不成立，故舍去. x2 y2 若m 7，设P(x，y)，则  1 ，所以 7 3 y3 2  1  2 x7 ， 因为 2 x4  y3 2  2 x4  1  2 x7 ≤ 0 ，所以x0， y   3 ，………………………………15分 所以 O D  1 2 ( A P  P B )  7 . 所以 DO 的最大值是 7，当且仅当O，M，P三点共线时等号成立. ……………17分 另解：设P(mcos，m24sin)，因为点P是椭圆C内（包括边界）的一个动点， {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}所以 试卷第7页，共7页 m 2 c o4 s 2 ( m 2 43 ) s in 2 1     ≤ ， 所以 ( m 2 1 6 ) s in 2 3 m 2 1 2    ≤ ， 所以 ( m 2  1 6 )  3 m 2 ≤ 1 2 ，所以m2≤7，所以m≤ 7 . 当 P ( 0 ，  3 ) 时， D O 取得最大值是 7 . ………………………………17分 {{##{{QQQQAABBaYQQYaQ8xgggAAYogAIJbIAACAJR5gqCBAUQHWkCQgCiQgsOIAQjJkKBoEECQCQCCoGDhuAAARELsCAJAFIBBSIAA=F}A#B}AA=}#}