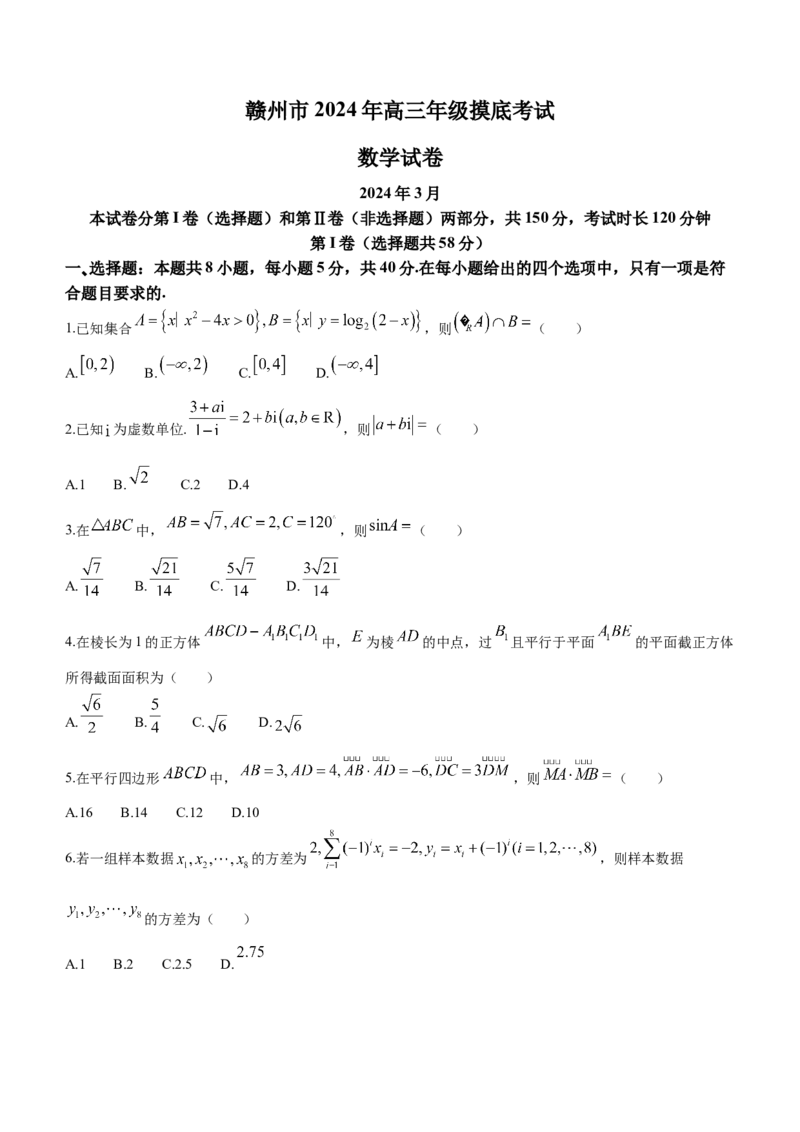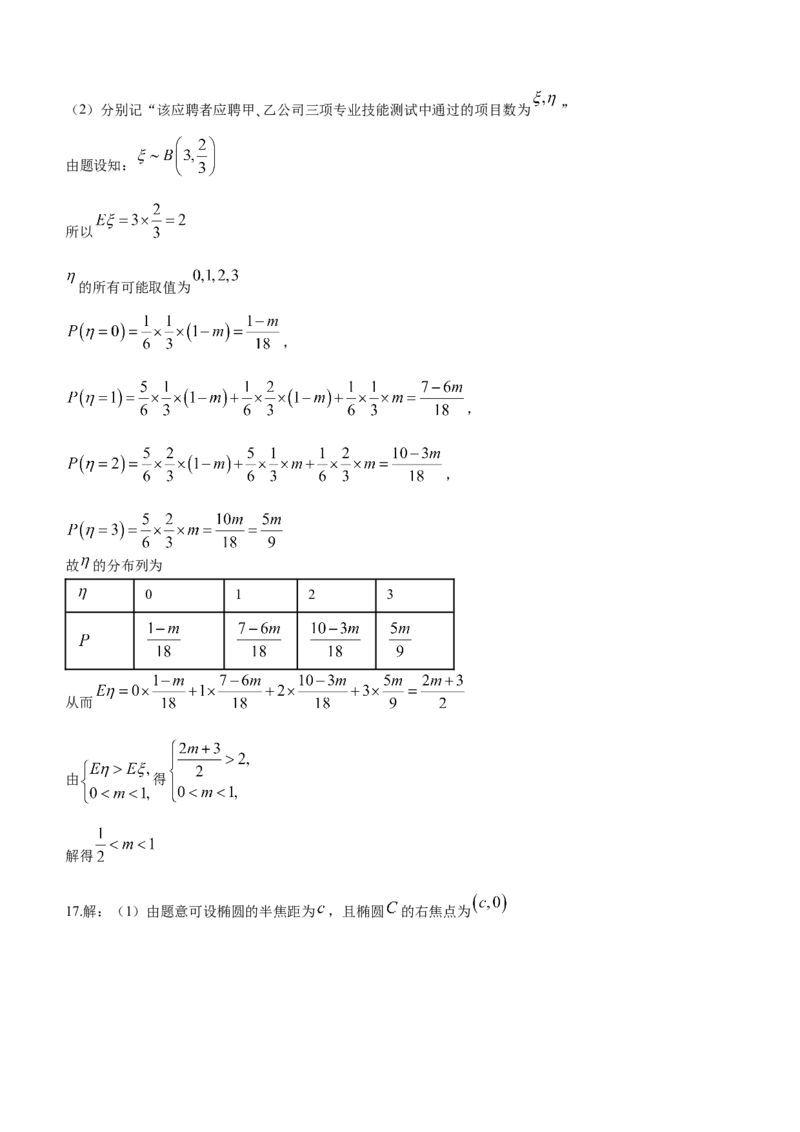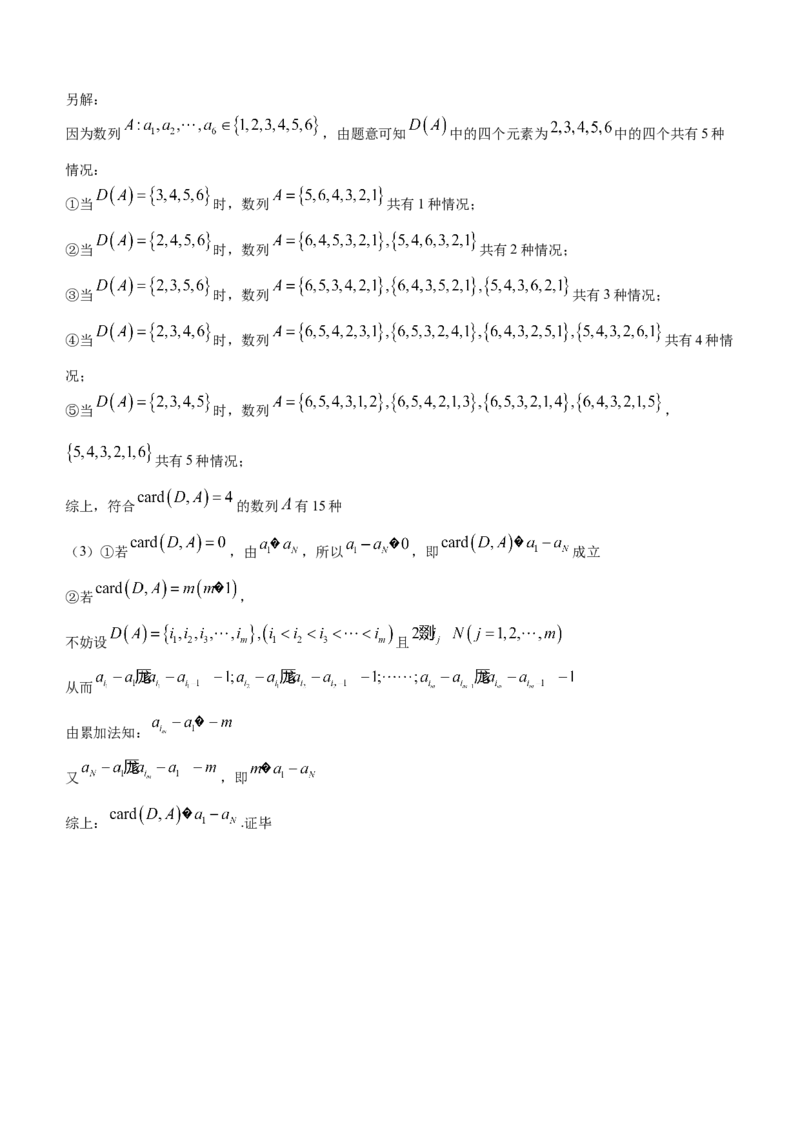文档内容
赣州市 2024 年高三年级摸底考试
数学试卷
2024年3月
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时长120分钟
第I卷(选择题共58分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.已知 为虚数单位. ,则 ( )
A.1 B. C.2 D.4
3.在 中, ,则 ( )
A. B. C. D.
4.在棱长为1的正方体 中, 为棱 的中点,过 且平行于平面 的平面截正方体
所得截面面积为( )
A. B. C. D.
5.在平行四边形 中, ,则 ( )
A.16 B.14 C.12 D.10
6.若一组样本数据 的方差为 ,则样本数据
的方差为( )
A.1 B.2 C.2.5 D.
学科网(北京)股份有限公司7.已知 ,则( )
A. B.
C. D.
8.在边长为4的正方体 中,点 是 的中点,点 是侧面 内的动点(含四条
边),且 ,则 的轨迹长度为( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得3分,有选错的得0分.
9.已知等比数列 的前 项和为 ,则( )
A. B.
C.数列 为单调数列 D.数列 为单调数列
10.已知函数 ,则( )
A. 是 的一个周期 B. 的图象关于原点对称
C. 的图象过点 D. 为 上的单调函数
11.曲线 是平面内与两个定点 的距离的积等于 的点 的轨迹,则( )
A.曲线 关于坐标轴对称 B. 周长的最小值为
C. 到 轴距离的最大值为 D. 到原点距离的最小值为
第Ⅱ卷(非选择题共92分)
三、填空题:本题共3小题,每小题5分,共15分.
12.求值: __________.
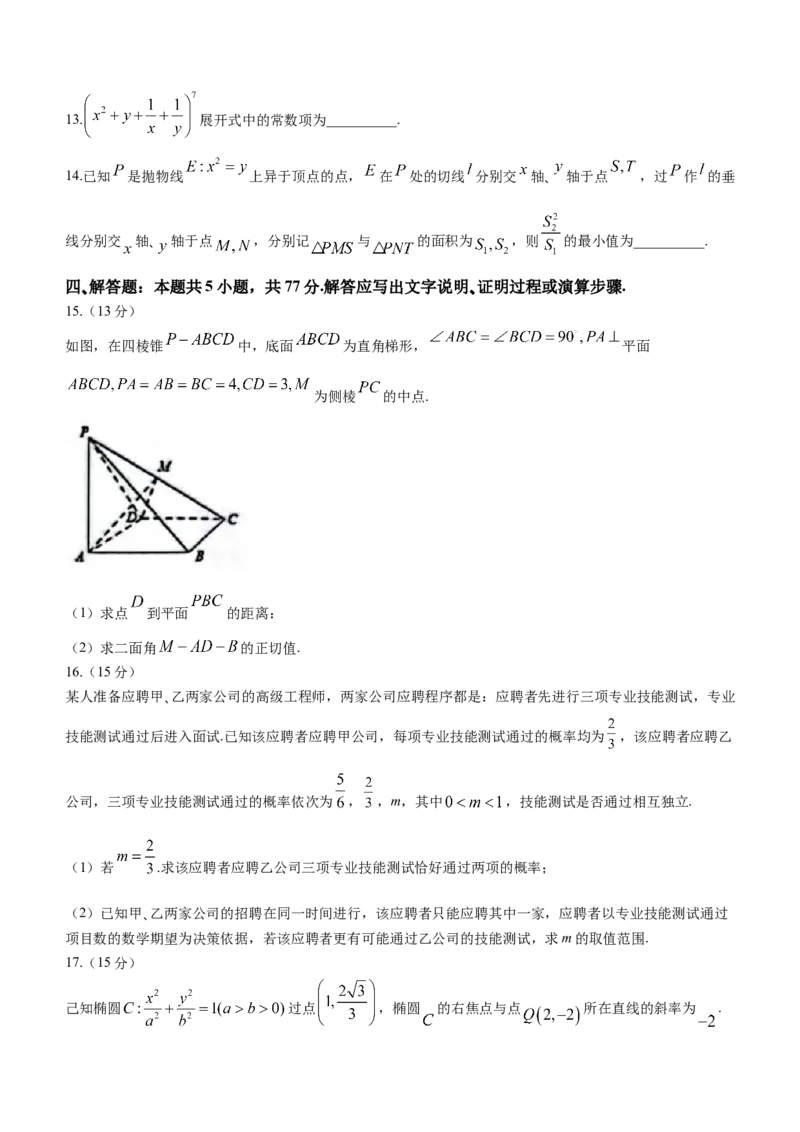
学科网(北京)股份有限公司13. 展开式中的常数项为__________.
14.已知 是抛物线 上异于顶点的点, 在 处的切线 分别交 轴、 轴于点 ,过 作 的垂
线分别交 轴、 轴于点 ,分别记 与 的面积为 ,则 的最小值为__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
如图,在四棱锥 中,底面 为直角梯形, 平面
为侧棱 的中点.
(1)求点 到平面 的距离:
(2)求二面角 的正切值.
16.(15分)
某人准备应聘甲、乙两家公司的高级工程师,两家公司应聘程序都是:应聘者先进行三项专业技能测试,专业
技能测试通过后进入面试.已知该应聘者应聘甲公司,每项专业技能测试通过的概率均为 ,该应聘者应聘乙
公司,三项专业技能测试通过的概率依次为 , ,m,其中 ,技能测试是否通过相互独立.
(1)若 .求该应聘者应聘乙公司三项专业技能测试恰好通过两项的概率;
(2)已知甲、乙两家公司的招聘在同一时间进行,该应聘者只能应聘其中一家,应聘者以专业技能测试通过
项目数的数学期望为决策依据,若该应聘者更有可能通过乙公司的技能测试,求m的取值范围.
17.(15分)
己知椭圆 过点 ,椭圆 的右焦点与点 所在直线的斜率为 .
学科网(北京)股份有限公司(1)求椭圆 的方程;
(2)若过 的直线 与椭圆 交于 两点.点 .直线 分别交椭圆 于点 ,直线
的斜率是否为定值?若是,求出该定值,若不是,请说明理由.
18.(17分)
已知函数 .
(1)求 的单调区间,
(2)已如 .若函数 有唯一的零点 .证明, .
19.(17分)
设数列 .如果对小于 的每个正整数 都有 .则称 是数列 的一个
“ 时刻”.记 是数列 的所有“ 时刻”组成的集合, 的元素个数记为 .
(1)对数列 ,写出 的所有元素;
(2)数列 满足 ,若 .求数列 的种数.
(3)证明:若数列 满足 ,则 .
学科网(北京)股份有限公司赣州市 2024 年高三年级摸底考试
数学(理科)参考答案
一、单选题(共40分)
题号 1 2 3 4 5 6 7 8
答案 A B B A A C D D
二、多选题(共18分)
题号 9 10 11
答案 BC ABC ABD
三、填空题(共15分)
12. 13.630 14.1
四、解答题(共77分)
15.解:(1)由 平面 ,可得
学科网(北京)股份有限公司令点 到平面 的距离为 ,则
由 ,可得
则
由 ,可得:
由 平面 ,可得 ,则
则 ,即点 到平面 的距离为
(2)设 为 的中点,过 作 交 于 ,连结
是 的中点, 平面
平面 ,
为二面角 的一个平面角
又 ,
且 ,可得
则
即二面角 的正切值为
说明:也可以利用向量法!
16.解:(1)记“该应聘者应聘乙公司三项专业技能测试恰好通过两项”为事件
由题设
学科网(北京)股份有限公司(2)分别记“该应聘者应聘甲、乙公司三项专业技能测试中通过的项目数为 ”
由题设知:
所以
的所有可能取值为
,
,
,
故 的分布列为
0 1 2 3
从而
由 得
解得
17.解:(1)由题意可设椭圆的半焦距为 ,且椭圆 的右焦点为
学科网(北京)股份有限公司由题意得:
解得
所以 的方程为:
(2)设 的方程为 ,设 ,则直线 的方程为
由 可得
结合 ,可得
可得 ,解得
代入 ,解得
同理可得
故
学科网(北京)股份有限公司,故直线 的斜率是定值,且定值为2
18.解:(1)
当 时, 为增函数
又
当 时, 单调递减;
当 时, 单调递增.
的减区间为 ,增区间为
(2)
由(1)可知 在 单调递增,且 ,
又
存在唯一的 使得
当 时 单调递减;当 时 单调递增;
若方程 有唯一的实数 ,则
学科网(北京)股份有限公司消去 可得
令 ,
则
在 上为减函数
且
当 时 ,即
19.解:(1)由题设知当 时, ,故 是数列 的一个“ 时刻”
同理当 时,都有 ,即 也是数列 的一个“ 时刻”
综上,
(2)由 ,易知 或
①当 时, 必须从左往右排列,6可以是 中任一个,共有5种情况
②当 时,若 中的四个元素是由集合 中的元素 或 或 或 引起的
1.若由 引起,即4,3,2,1从左往右排列,则5必须排在4的后面,共4种;
2.若由 引起,即5,3,2,1从左往右排列,则4必须排在3的后面,共3种
3.若由 引起,即 从左往右排列,则3必须排在2的后面,共2种;
4.若由 引起,即 从左往右排列,则2必须排在1的后面,共1种
综上,符合 的数列 有15种
学科网(北京)股份有限公司另解:
因为数列 ,由题意可知 中的四个元素为 中的四个共有5种
情况:
①当 时,数列 共有1种情况;
②当 时,数列 共有2种情况;
③当 时,数列 共有3种情况;
④当 时,数列 共有4种情
况;
⑤当 时,数列 ,
共有5种情况;
综上,符合 的数列 有15种
(3)①若 ,由 ,所以 ,即 成立
②若 ,
不妨设 且
从而
由累加法知:
又 ,即
综上: .证毕
学科网(北京)股份有限公司