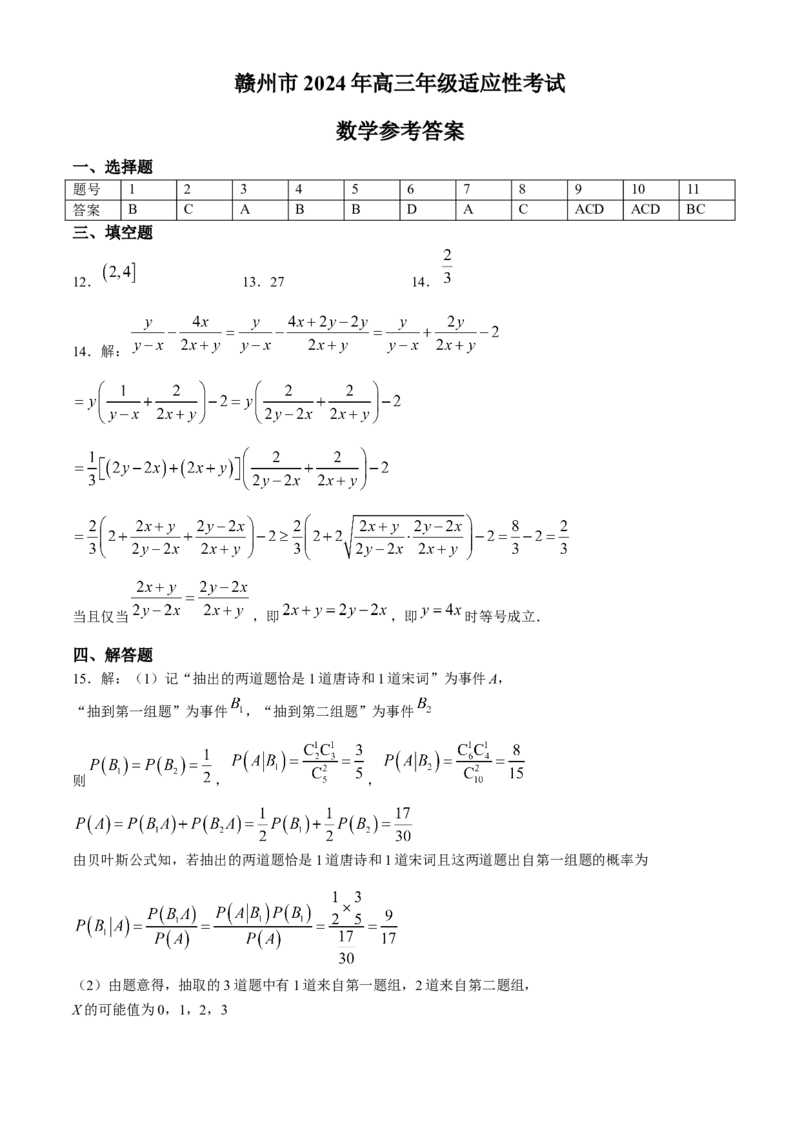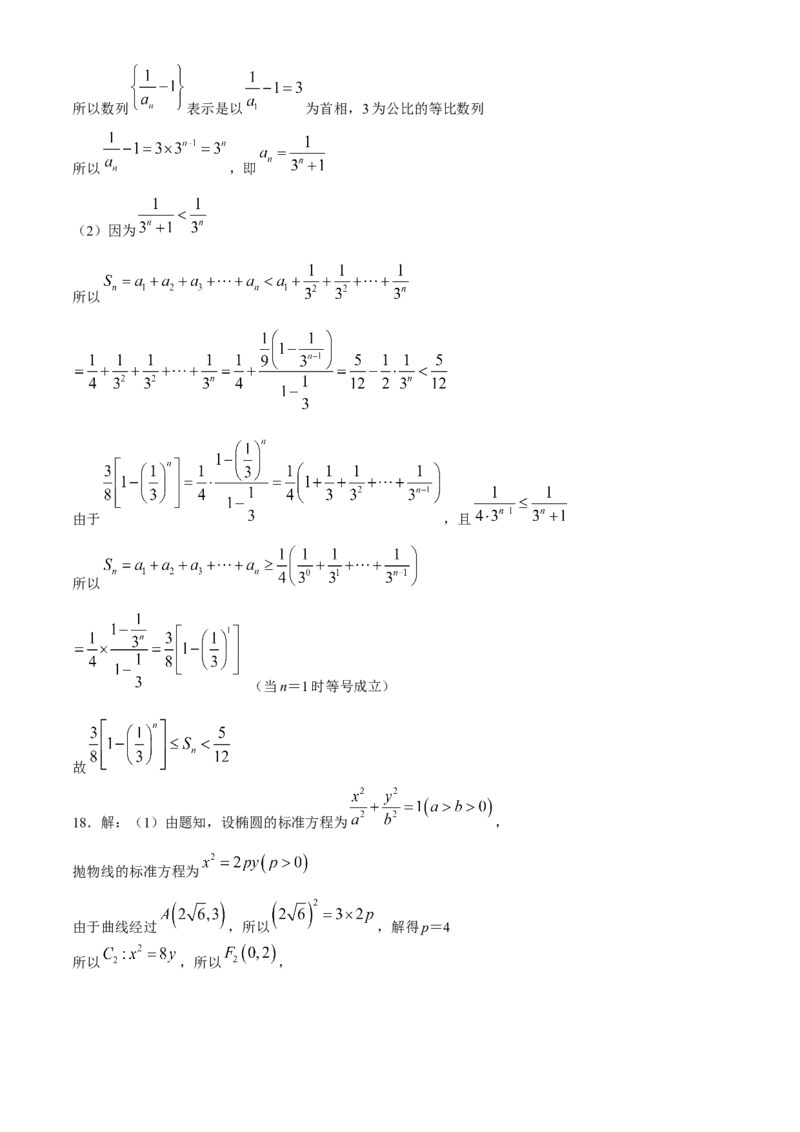文档内容
赣州市 2024 年高三年级适应性考试
数学试卷
2024年5月
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.在等差数列 中. , 是方程 的两根,则 的前6项和为( )
A.48 B.24 C.12 D.8
2.已知甲、乙两组数据分别为:22,21,24,23,25,20和25,22,a,26,23,24.若乙组数据的平均
数比甲组数据的平均数大2,则( )
A.甲、乙两组数据的极差不同 B.乙组数据的中位数为24
C.甲、乙两组数据的方差相同 D.甲组数据的第一四分位数为21.5
3.记 的内角A,B,C的对边分别为a,b,c,若b=1, ,则A=( )
A. B. C. D.
4.已知直线 .圆 ,则( )
A.l过定点 B.l与C一定相交
C.若l平分C的周长,则m=1 D.l被C截得的最短弦的长度为4
5.由0和1组成的序列称为0-1序列,序列中数的个数称为这个序列的长度,如01011是一个长度为5
的0-1序列.在长度为8的0-1序列中.所有1互不相邻的序列个数为( )
A.20 B.54 C.55 D.280
6.已知 , 为双曲线 的左、右焦点,M为C左支上一点.设
, ,且 ,则C的离心率为( )
A. B.3 C.2 D.
7.已知球O内切于正四棱锥P-ABCD,PA=AB=2,EF是球O的一条直径,点Q为正四棱锥表面上的
点,则 的取值范围为( )
A. B. C. D.
学科网(北京)股份有限公司8.已知函数 , .若 ,则k的取值范围为( )
A. B. C. D.
二、多选题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知i为虚数单位, ,则( )
A.
B.
C.若 ,则 的最大值为6
D.若 是关于x的方程 的一个根,则q=8
10.已知函数 ,则( )
A.若 相邻两条对称轴的距离为 ,则
B.当 的最小正周期为 , 时,
C.当 时, 的图象向右平移 个单位长度得到函数解析式为
D.若 在区间 上有且仅有两个零点,则
11.函数 及其导函数 的定义域均为R, 和 都是奇函数,则( )
A. 的图象关于直线 对称 B. 的图象关于点 对称
C. 是周期函数 D.
三、填空题:本大题共3小题,每小题5分,共15分.
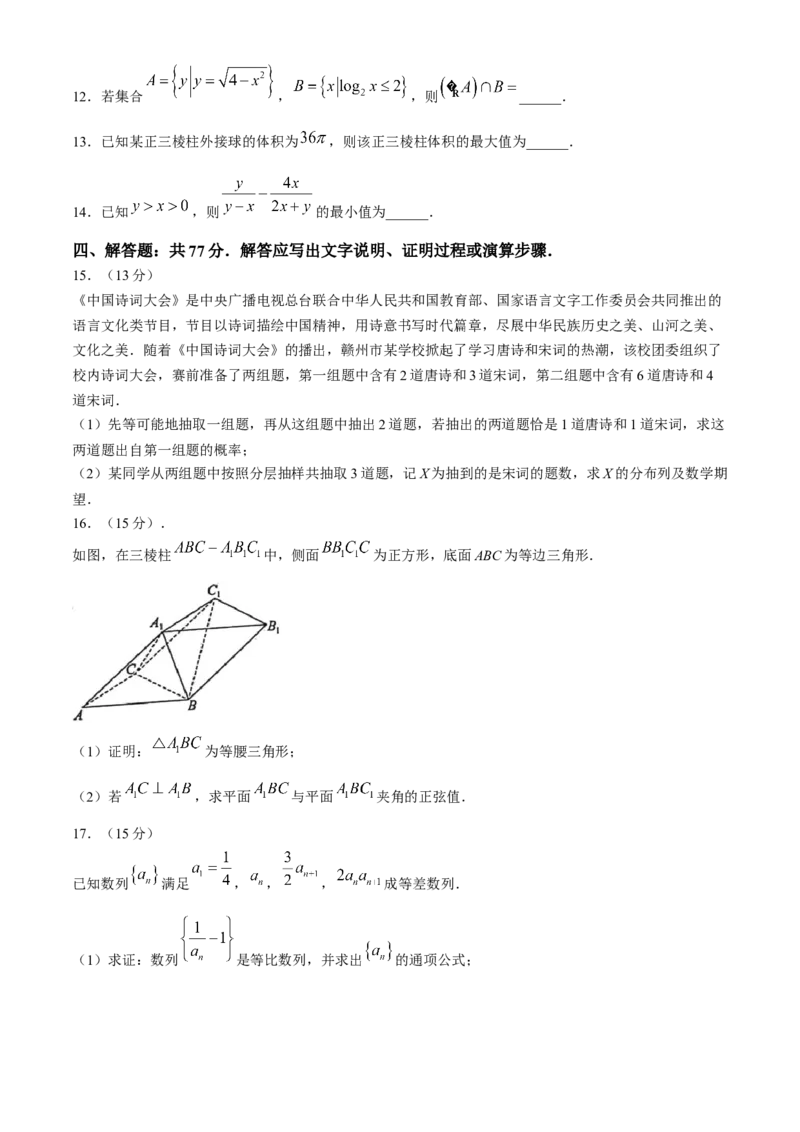
学科网(北京)股份有限公司12.若集合 , ,则 ______.
13.已知某正三棱柱外接球的体积为 ,则该正三棱柱体积的最大值为______.
14.已知 ,则 的最小值为______.
四、解答题:共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
《中国诗词大会》是中央广播电视总台联合中华人民共和国教育部、国家语言文字工作委员会共同推出的
语言文化类节目,节目以诗词描绘中国精神,用诗意书写时代篇章,尽展中华民族历史之美、山河之美、
文化之美.随着《中国诗词大会》的播出,赣州市某学校掀起了学习唐诗和宋词的热潮,该校团委组织了
校内诗词大会,赛前准备了两组题,第一组题中含有2道唐诗和3道宋词,第二组题中含有6道唐诗和4
道宋词.
(1)先等可能地抽取一组题,再从这组题中抽出2道题,若抽出的两道题恰是1道唐诗和1道宋词,求这
两道题出自第一组题的概率;
(2)某同学从两组题中按照分层抽样共抽取3道题,记X为抽到的是宋词的题数,求X的分布列及数学期
望.
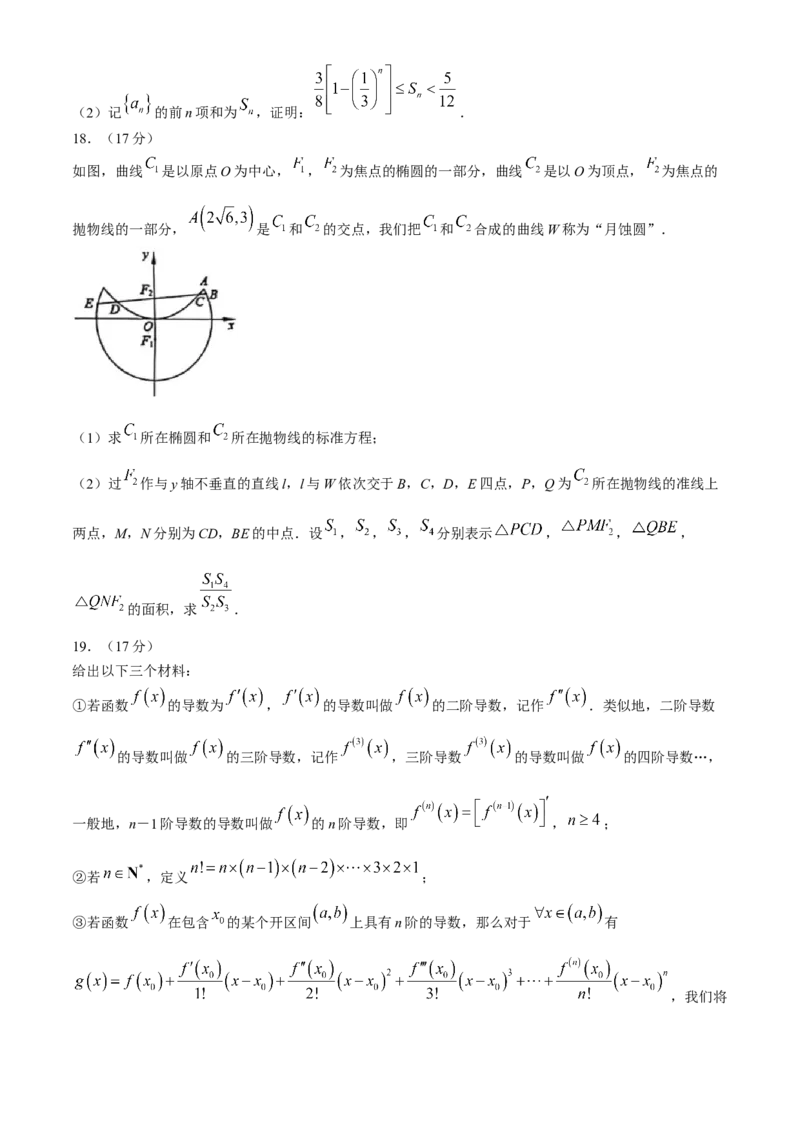
16.(15分).
如图,在三棱柱 中,侧面 为正方形,底面ABC为等边三角形.
(1)证明: 为等腰三角形;
(2)若 ,求平面 与平面 夹角的正弦值.
17.(15分)
已知数列 满足 , , , 成等差数列.
(1)求证:数列 是等比数列,并求出 的通项公式;
学科网(北京)股份有限公司(2)记 的前n项和为 ,证明: .
18.(17分)
如图,曲线 是以原点O为中心, , 为焦点的椭圆的一部分,曲线 是以O为顶点, 为焦点的
抛物线的一部分, 是 和 的交点,我们把 和 合成的曲线W称为“月蚀圆”.
(1)求 所在椭圆和 所在抛物线的标准方程;
(2)过 作与y轴不垂直的直线l,l与W依次交于B,C,D,E四点,P,Q为 所在抛物线的准线上
两点,M,N分别为CD,BE的中点.设 , , , 分别表示 , , ,
的面积,求 .
19.(17分)
给出以下三个材料:
①若函数 的导数为 , 的导数叫做 的二阶导数,记作 .类似地,二阶导数
的导数叫做 的三阶导数,记作 ,三阶导数 的导数叫做 的四阶导数…,
一般地,n-1阶导数的导数叫做 的n阶导数,即 , ;
②若 ,定义 ;
③若函数 在包含 的某个开区间 上具有n阶的导数,那么对于 有
,我们将
学科网(北京)股份有限公司称为函数 在点 处的n阶泰勒展开式.例如, 在点 处的n阶泰勒展开式为
.根据以上三段材料,完成下面的题目:
(1)若 , 在点 处的3阶泰勒展开式分别为 , ,求出 ,
;
(2)比较(1)中 与 的大小;
(3)证明: .
学科网(北京)股份有限公司赣州市 2024 年高三年级适应性考试
数学参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B C A B B D A C ACD ACD BC
三、填空题
12. 13.27 14.
14.解:
当且仅当 ,即 ,即 时等号成立.
四、解答题
15.解:(1)记“抽出的两道题恰是1道唐诗和1道宋词”为事件A,
“抽到第一组题”为事件 ,“抽到第二组题”为事件
则 , ,
由贝叶斯公式知,若抽出的两道题恰是1道唐诗和1道宋词且这两道题出自第一组题的概率为
(2)由题意得,抽取的3道题中有1道来自第一题组,2道来自第二题组,
X的可能值为0,1,2,3
学科网(北京)股份有限公司所以X的分布列为
X 0 1 2 3
P
所以
16.解:(1)设BC, 的中点分别为O,M,连接OM,AO, ,
由于侧面 为正方形,所以 ,
∵ ,∴
由于底面ABC为等边三角形,所以
又 , ,
所以
由于 , ,故四边形 为平行四边形,
又 ,故
由于O是BC中点,所以 ,则 为等腰三角形
(2)不妨设AB=2,则 ,CO=BO=1,
又 ,且 ,则
学科网(北京)股份有限公司则 ,从而 ,而 , ,
则 ,OA,OB两两垂直,
故可建立如图所示的空间直角坐标系 ,
则 , , , ,
则 ,
设平面 的一个法向量为 ,
则 取 ,则
由于平面 的一个法向量为 ,
故
设所求角为 , , ,
故平面 与平面 的夹角的正弦值为
17.证明:(1)由于 , , 成等差数列,所以
即 ,可得
学科网(北京)股份有限公司所以数列 表示是以 为首相,3为公比的等比数列
所以 ,即
(2)因为
所以
由于 ,且
所以
(当n=1时等号成立)
故
18.解:(1)由题知,设椭圆的标准方程为 ,
抛物线的标准方程为
由于曲线经过 ,所以 ,解得p=4
所以 ,所以 ,
学科网(北京)股份有限公司所以 ,且 ,
解得 , ,所以
(2)由题意可知直线l的斜率必存在且不为0,
设 , , , ,
联立 可得
可得
联立 可得 ,可得
记 , , , 的高分别为 , , , ,
由于 , ,
所以
19.解:(1)∵ , ,
∴ , , ,
学科网(北京)股份有限公司∴
同理可得:
(2)由(1)知: , ,
令 ,则 ,
∴ ,∴ 在R上单调递增
又 ,∴ 在 上单调递减,在 上单调递增,
∴ ,即
故
(3)令 ,则
由(2)知, ,所以 在R上单调递增,又 ,
所以当 时, , ;
当 时, , ;
当 时, ,
∴ 在点 处的4阶泰勒展开式为: ,
∴ ,当且仅当x=0时取等号
①当 时, ,当且仅当x=0时取等号,
学科网(北京)股份有限公司所以
②当 时,设 , ,
, ,
若 ,由于 ,所以,
,
,从而
若 , ,
所以, 时, 单调递减,从而 ,即 .
综上: .
学科网(北京)股份有限公司