新结构江苏省南通市2024届新高考适应性调研试题答案解析(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套

【新结构】江苏省南通市 2024 届新高考适应性调研试题 答案和解析 【答案】 1. B 2. A 3. D 4. D 5. D 6. B 7. B 8. A 9. BC 10. BD 11. ACD 12. 18 4 3 13. π ； π 3 14. 7 −2a2x2 +ax+1 15. 解：(1)函数定义域为(0,+∞)， f′(x)= x 1 因为x=1是函数 y = f(x)的极值点，所以 f′(1)=1+a−2a2 =0，解得a=− 或a =1， 2 因为a0，所以a=1. −2x2 +x+1 −(2x+1)(x−1) 此时 f′(x)= = x x f′( x )>0得0< x<1函数单调递增， f′( x )<0得x>1函数单调递减， 所以x=1是函数的极大值. 所以a=1. 1 (2)若a=0， f′(x)= >0， x 则函数 f (x)的单调增区间为(0,+∞); −2a2x2 +ax+1 (2ax+1)(−ax+1) 若a>0， f′(x)= = ， x x 因为a>0，x>0，则2ax+1>0， 1 由 f′(x)>0，结合函数的定义域，可得0< x< ; a 1 由 f′(x)<0，可得x> ; a 第1页，共16页 学科网（北京）股份有限公司1 1 ∴函数的单调增区间为(0, );单调减区间为( ,+∞). a a 综上可知：当a=0时，函数 f (x)在(0,+∞)上单调递增，无递减； 1 1 当a>0时，函数 f (x)在(0, )上单调递增，在( ,+∞)上单调递减. a a 16. 解：(1)前4局A都不下场说明前4局A都获胜， 1 1 1 1 1 故前4局A都不下场的概率为P= × × × = . 2 2 2 2 16 (2)X 的所有可能取值为0，1，2，3，4， 1 1 1 其中，X =0表示第1局B输，第4局是B上场，且B输，则P(X =0)= × = ； 2 2 4 X =1表示第1局B输，第4局是B上场，且B赢；或第1局B赢，且第2局B输， 1 1 1 1 1 则P(X =1)= × + × = ； 2 2 2 2 2 X =2表示第1局B赢，且第2局B赢，第3局B输， 1 1 1 1 则P(X =2)= × × = ； 2 2 2 8 X =3表示第1局B赢，且第2局B赢，第3局B赢，第4局B输， 1 1 1 1 1 则P(X =3)= × × × = ； 2 2 2 2 16 X =4表示第1局B赢，且第2局B赢，第3局B赢，第4局B赢， 1 1 1 1 1 则P(X =4)= × × × = . 2 2 2 2 16 所以X的分布列为 X 0 1 2 3 4 1 1 1 1 1 P 4 2 8 16 16 1 1 1 1 1 19 故X的数学期望为E(X)=0× +1× +2× +3× +4× = . 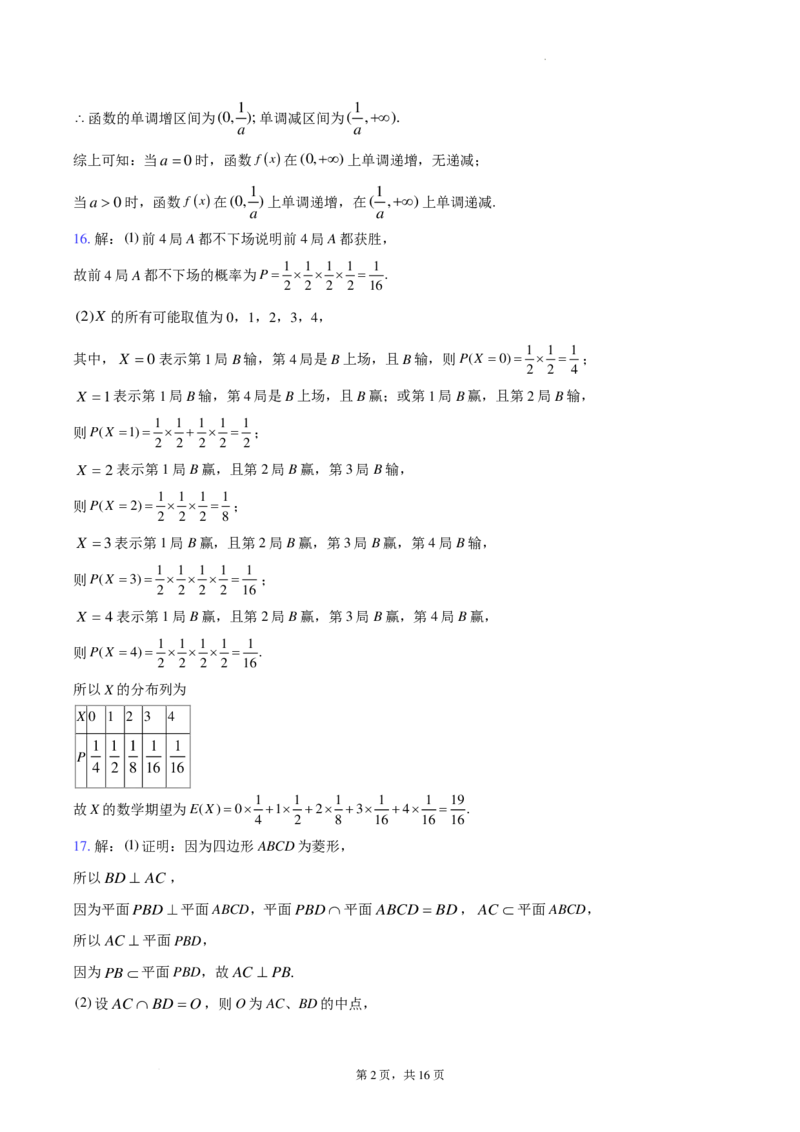4 2 8 16 16 16 17. 解：(1)证明：因为四边形ABCD为菱形， 所以BD⊥ AC， 因为平面PBD⊥平面ABCD，平面PBD∩平面ABCD = BD，AC ⊂平面ABCD， 所以AC ⊥平面PBD， 因为PB⊂平面PBD，故AC ⊥ PB. 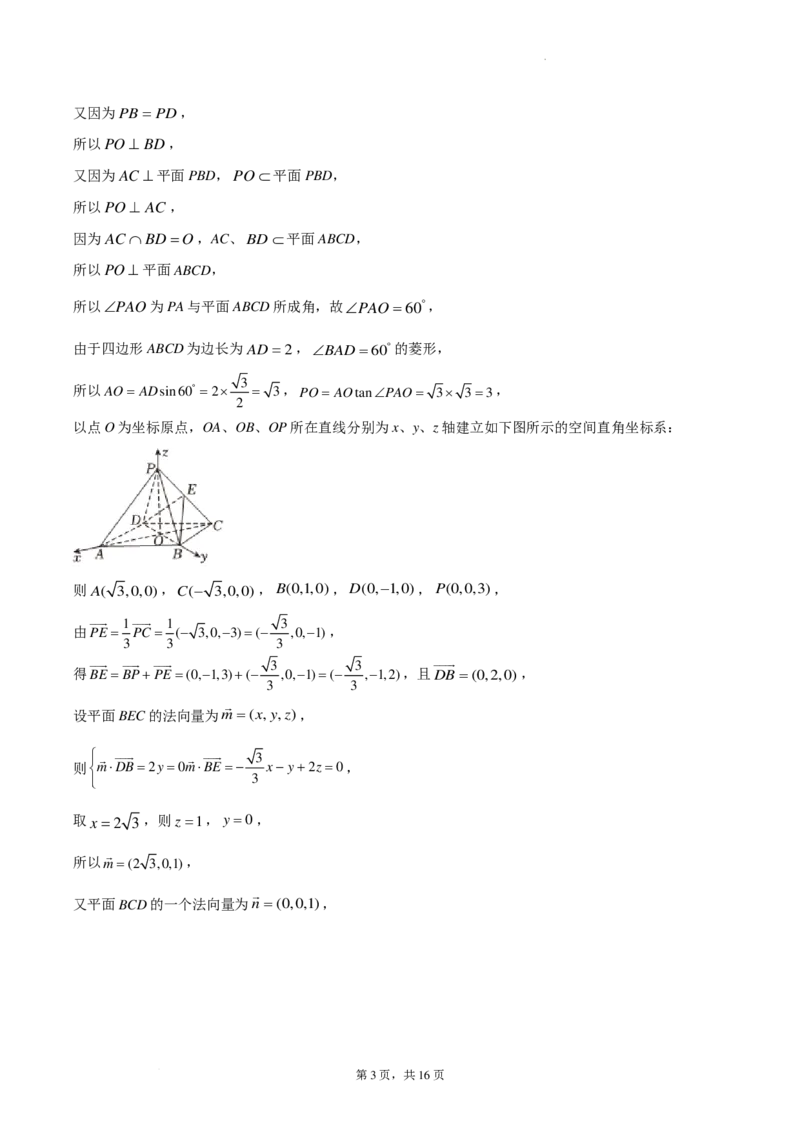(2)设 AC∩BD=O，则O为AC、BD的中点， 第2页，共16页 学科网（北京）股份有限公司又因为PB = PD， 所以PO⊥ BD， 又因为AC ⊥平面PBD，PO⊂平面PBD， 所以PO⊥ AC， 因为AC∩BD=O，AC、BD⊂平面ABCD， 所以PO⊥平面ABCD， 所以∠PAO为PA与平面ABCD所成角，故∠PAO=60°， 由于四边形ABCD为边长为 AD=2，∠BAD=60°的菱形， 3 所以AO= ADsin60° =2× = 3， PO= AOtan∠PAO= 3× 3=3 ， 2 以点O为坐标原点，OA、OB、OP所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系： 则 A( 3,0,0)，C(− 3,0,0)，B(0,1,0)，D(0,−1,0)，P(0,0,3)，   1 1 3 由PE= PC = (− 3,0,−3)=(− ,0,−1)， 3 3 3     3 3 得BE=BP+PE=(0,−1,3)+(− ,0,−1)=(− ,−1,2)，且DB=(0,2,0)， 3 3  设平面BEC的法向量为m=(x,y,z)，     3 则m⋅DB=2y=0m⋅BE=− x− y+2z=0，  3 取x=2 3，则z =1，y=0，  所以m=(2 3,0,1)，  又平面BCD的一个法向量为n =(0,0,1)， 第3页，共16页 学科网（北京）股份有限公司    |m⋅n| 1 13 所以|cos〈m,n〉|=   = = ， |m|⋅|n| 13×1 13 13 所以平面EBD与平面BCD的夹角的余弦值为 . 13 3 c 3 18. 解：(Ⅰ)离心率为 ，|FF |=2 3，∴ = 2c=2 3， 2 1 2 a 2 ∴a=2，c= 3，则b=1， x2 ∴椭圆C的方程的方程为： + y2 =1. 4 (Ⅱ)由(Ⅰ)得A(−2,0)， A (2,0)， 1 2 m m 直线PA ，PA 的方程分别为：y= (x+2)， y = (x−2)， 1 1 6 2  m x2 由y= (x+2) + y2 =1得(9+m2)x2 +4m2x+4m2 −36=0，  6 4 −4m2 18−2m2 m 6m ∴−2+x = ，可得.x = ，y = (x +2)= M 9+m2 M 9+m2 M 6 M 9+m2  m x2 由y= (x−2) + y2 =1，可得(1+m2)x2 −4mx+4m2 −4=0，  2 4 4m2 2m2 −2 m −2m ∴2+x = ，可得x = ，y = (x −2)= ， N 1+m2 N 1+m2 N 2 N 1+m2 y − y 2m k = M N = ， MN x −x 3−m2 M N −2m 2m 2m2 −2 直线MN的方程为：y− = (x− )， 1+m2 3−m2 1+m2 2m 2m2 −2 2m 2m 2m2 −2 3−m2 2m y= (x− )− = (x− − )= (x−1)， 3−m2 1+m2 1+m2 3−m2 1+m2 1+m2 3−m2 可得直线MN过定点(1,0)，故设MN的方程为：x=ty+1，  x2 由x=ty+2 + y2 =1得(t2 +4)y2 +2ty−3=0，  4 −2t −3 设M(x ,y )，N(x ,y )，则 y + y = ， y y = ， 1 1 2 2 1 2 t2 +4 1 2 t2 +4 4 t2 +3 | y − y |= (y + y )2 −4y y = ， 1 2 1 2 1 2 t2 +4 第4页，共16页 学科网（北京）股份有限公司1 t2 +3 ∴OMN 的面积S = ×1×(y − y )=2 ， 2 1 2 t2 +4 2d 2 s= = 令 t2 +3=d,(d 3)，则 d2 +1 d + 1 ， d 1 d 3，且函数 f(d)=d + 在[ 3,+∞)递增， d 3 ∴当d = 3，s取得最小值 . 2 19. 解：(1) A =(1 2 32 3 13 1 2) 是 Γ 数表， 3 3 d(a ,a )+d(a ,a )=2+3=5. 1,1 2,2 2,2 3,3 (2)由题可知 d(a ,a )=|a −a |+|a −a |=1 (i=1,2,3; j=1,2,3) . i,j i+1,j+1 i,j i+1,j i+1,j i+1,j+1 当 a =1 时，有 d(a ,a )=|a −1|+|a −1|=1 ， i+1,j i,j i+1,j+1 i,j i+1,j+1 所以 a +a =3 . i,j i+1,j+1 当 a =2 时，有 d(a ,a )=|a −2|+|a −2|=1 ， i+1,j i,j i+1,j+1 i,j i+1,j+1 所以 a +a =3 . i,j i+1,j+1 所以 a +a =3(i=1,2,3; j=1,2,3). i,j i+1,j+1 所以 a +a +a +a =3+3=6, a +a =3,a +a =3. 1,1 2,2 3,3 4,4 1,3 2,4 3,1 4,2 a +a +a =3+1=4 或者 a +a +a =3+2=5 ， 1,2 2,3 3,4 1,2 2,3 3,4 a +a +a =3+1=4 或者 a +a +a =3+2=5 ， 2,1 3,2 4,3 2,1 3,2 4,3 a =1 或 a =2 ， a =1 或 a =2 ， 1,4 1,4 4,1 4,1 故各数之和 6+3+3+4+4+1+1=22 ， 当 A =(1 1 1 11 2 2 21 2 1 11 2 1 2) 时，各数之和取得最小值 22 . 4 (3)由于 Γ 数表 A 中共 100 个数字， 4 10 必然存在 k∈{1,2,3,4} ，使得数表中 k 的个数满足 T25. 设第 i 行中 k 的个数为 r(i=1,2,⋅⋅⋅,10). i 第5页，共16页 学科网（北京）股份有限公司当 r2 时，将横向相邻两个 k 用从左向右的有向线段连接， i 则该行有 r −1 条有向线段， i i=1 所以横向有向线段的起点总数 R=∑(r −1) ∑ (r −1)=T −10. i i ri2 10 设第 j 列中 k 的个数为 c (j=1,2,⋅⋅⋅,10) . j 当 c2 时，将纵向相邻两个 k 用从上到下的有向线段连接， j 则该列有 c −1 条有向线段， j j=1 所以纵向有向线段的起点总数 C =∑(c −1) ∑ (c −1)=T −10. j j cj2 10 所以 R+C2T −20 ， 因为 T25 ，所以 R+C−T2T −20−T =T −20>0 . 所以必存在某个 k 既是横向有向线段的起点，又是纵向有向线段的终点， 即存在 10,b>0)的渐近线方程为 y =± x，所以 =3， a2 b2 a a 2 b 所以e= 1+  = 1+32 = 10. a 故答案为 A. 3. 【分析】 本题考查等差数列，属于基础题. a +a a +a S 2 9 = 1 10 = 10 利用 b b +b T 即可求解. 3 1 5 5 2 【解答】 S 8n 解：因为 2n = ， T 3n+5 n 10 (a +a ) a +a a +a 2 1 10 S 40 所以 2 9 = 1 10 = = 10 = =2. b b +b 5 T 20 3 1 5 (b +b ) 5 2 2 1 5 故答案选：D. 4. 【分析】 本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查空间想象能力、 推理论证能力，属基础题． 根据相关定理或性质逐一判定即可得出结论. 【解答】 解：对于A，由面面平行的定义可得n与β没有公共点，即n / / β，故A正确； 对于B，如果m⊥α，n//α，那么在α内一定存在直线b||n，又m⊥b，则m⊥n，故B正确； 对于C，如果m / / n，m⊥α，那么根据线面平行的性质可得 n⊥α，故C正确; 对于D，如果m⊥n，m⊥α，则n//α或n⊂α，又n//β，那么α与β可能相交，也可能平行，故D 第7页，共16页 学科网（北京）股份有限公司错误. 故选D. 5. 【分析】 本题考查排列、组合的综合应用，属于中档题. C2C2C2 由6人平均分3个不同组，共 6 4 2 ⋅3!=90种，排除甲在歌曲演唱小组，乙在歌曲诗歌创作小组的可能 3! 结果即可. 【解答】 C2C2C2 解：6人平均分3个不同组，共 6 4 2 ⋅3!=90种， 3! C1C2C2 甲在歌曲演唱小组，此时有 5 4 2 ⋅2!=30种， 2! C1C2C2 乙在歌曲诗歌创作小组，此时有 5 4 2 ⋅2!=30种， 2! 甲在歌曲演唱小组且乙在歌曲诗歌创作有A2 =12种， 4 故共有90−30−30+12=42种， 故选：D. 6. 【分析】 本题考查两直线平行的判定及其应用，考查充分、必要条件的判断，属于基础题. 根据两直线的位置关系、充分和必要条件的定义进行判断. 【解答】 解：当 l //l 时， (m−1)×2=m(m−1) ，解得 m=1 或 m=2 ， 1 2 经检验可知 m=1 或 m=2 都符合. 所以“ m=2 ”是“ l //l ”的充分不必要条件. 1 2 故选：B 7. 【分析】 本题考查两角和的余弦公式、诱导公式的应用，考查三角函数的化简求值，属于基础题. 根据两角和的余弦公式和诱导公式化简求值即可. 【解答】 2sinα sin2β 2sinβcosβ 2cosβ 解：由2tanα= = = = ， cosα sinβ+sin2β sinβ+sin2β 1+sinβ 第8页，共16页 学科网（北京）股份有限公司可得cosαcosβ=(1+sinβ)sinα，即cosαcosβ−sinαsinβ=sinα， π 得cos(α+β)=sinα=cos( −α)， 2 π π 因为α∈(0, )，β∈(0, )， 2 2 π 所以α+β= −α， 2 π π 5π π π 3 ∴2α+β= ，tan(2α+β+ )=tan =tan(− )=−tan =− . 2 3 6 6 6 3 故选B. 8. 【分析】 本题考查双曲线中的面积问题，属于较难题. 由题意画出图，由已知求出c的值，找出A,B的坐标，由AFF ,BFF ,FAB的内切圆圆心分别为 1 2 1 2 1 O,O ,O ，进行分析，由等面积法求出内切圆的半径，从而求出OO O 的底和高，利用三角形的面积 1 2 3 1 2 3 公式计算即可. 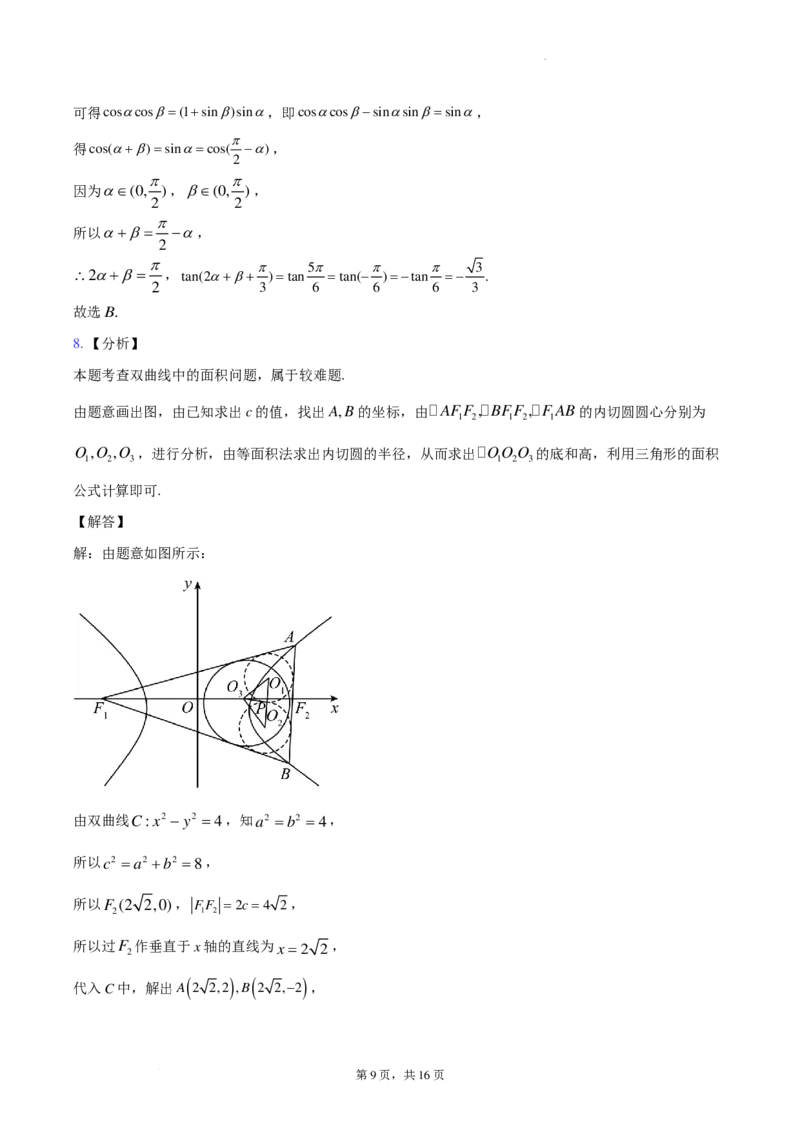【解答】 解：由题意如图所示： 由双曲线C:x2 − y2 =4，知a2 =b2 =4， 所以c2 =a2 +b2 =8， 所以F (2 2,0)， FF =2c=4 2， 2 1 2 所以过F 作垂直于x轴的直线为x=2 2， 2 ( ) ( ) 代入C中，解出A 2 2,2 ,B 2 2,−2 ， 第9页，共16页 学科网（北京）股份有限公司由题知AFF ,BFF 的内切圆的半径相等， 1 2 1 2 且| AF |=|BF |，AFF ,BFF 的内切圆圆心O,O 的连线垂直于x轴于点P， 1 1 1 2 1 2 1 2 设为r，在AFF 中，由等面积法得： 1 2 1( AF + AF + FF )⋅r = 1 FF ⋅ AF ， 2 1 2 1 2 2 1 2 2 由双曲线的定义可知： AF − AF =2a=4， 1 2 由 AF =2，所以 AF =6， 2 1 1( ) 1 所以 6+2+4 2 ⋅r = ×4 2×2， 2 2 ( ) 2 2× 2− 2 解得： r = 2 2 = =2 2−2 ， 2+ 2 2 因为FF 为FAB的∠AFB的角平分线， 1 2 1 1 所以O 一定在FF 上，即x轴上，令圆O 半径为R， 3 1 2 3 在AFB中，由等面积法得： 1 1( AF + BF + AB )⋅R= 1 FF ⋅ AB ， 2 1 1 2 1 2 又| AF |=|BF |=6， 1 1 1 1 所以 ×(6+6+4)⋅R= ×4 2×4， 2 2 所以R= 2 ， 所以 PF =r =2 2−2， 2 ( ) O P = O F − PF =R−r = 2− 2 2−2 =2− 2， 3 3 2 2 1 1 所以S = OO O P = ×2r× O P O1O2O3 2 1 2 3 2 3 ( ) ( ) =r× O P = 2 2−2 × 2− 2 =6 2−8. 3 故选 A. 9. 【分析】 第10页，共16页 学科网（北京）股份有限公司本题考查了三角函数的性质，属于基础题. 直接利用相应性质的判断方法判断即可. 【解答】 解：函数定义域为R关于原点对称， 又 f (−x)=sin −x + sin(−x) =sin x + sinx = f (x)， ∴ f(x)是偶函数，故A正确； 当x∈[−π,π] 时， f (x)={−2sinx,x∈[−π,0)2sinx,x∈[0,π], 易判断x∈[−π,π] 时，函数有3个零点，故C不正确； π  当x∈  ,π 时，函数单调递减，故B不正确；  2  π 显然sin|x|1，|sinx|1，存在x= 使得sin|x|=1，|sinx|=1，故 f (x)的最大值为2，故D正确. 2 10. 【分析】 本题考查复数代数形式的乘除运算，考查复数模的求法，属于一般题． 由复数的模及复数的基本概念判断B与D；举例判断A与C. 【解答】 解：取z =1，z =i，满足|z |=|z |，但z2 ≠ z2，，故A错误； 1 2 1 2 1 2 利用模的运算性质可知B正确； z 取z =1+i,z =1−i，则z z =2∈R，但 1 ∉R，故C错误； 1 2 1 2 z 2 设z =a+bi,z =c+di,(a,b,c,d∈R)， 1 2 z z = ac−bd +( ad +bc ) i = ( ac−bd )2 +( ad +bc )2 1 2 = a2c2 +a2d2 +b2c2 +b2d2 ， z ⋅ z = a2 +b2 ⋅ c2 +d2 = a2c2 +a2d2 +b2c2 +b2d2 ， 1 2 即 z z = z ⋅ z ，故D正确． 1 2 1 2 故选：BD. 11. 【分析】 第11页，共16页 学科网（北京）股份有限公司本题考查抽象函数的奇偶性、对称性及周期性，属于难题. 令x= y =0可判断A；若 f (x)为偶函数，令x=0， y =−1可得 f ( 1 )=0，与已知矛盾，从而可判断 B；取x=0，得到 f (−x )=−f ( x ) ，结合 f(2x+ 3 )为偶函数可判断C；由C可得 f ( x ) 的周期为6，对 2 3 称轴为x= ，从而可得 f (1)+ f (2)+ f (3)+ f (4)+ f (5)+ f (6)=0，根据周期性可判断D. 2 【解答】解：令x= y =0，可得 f (0) f (0)=0，解得 f(0)=0，故A正确； 若 f (x)为偶函数，令x=0， y =−1，可得 f (−1) f (1)= f2(0)− f2(−1)，即 f2(−1)+ f (−1) f (1)=0， 则 f2(1)+ f (1) f (1)=0，解得 f ( 1 )=0，与 f(1)= 3矛盾，故 f (x)不是偶函数，故B错误； 取x=0，可得 f(y)f(−y)=−f 2(y)，化得 f(y)[f(y)+ f(−y)]=0， 则 f(y)=0或 f(y)=−f(−y)， 易知若 f(y)=0，则 f(−y)=0，可得 f(y)=−f(−y)恒成立，即 f (x)为奇函数. 3  3  3 因为 f(2x+ )为偶函数，所以 f 2x+ = f −2x+ ， 2  2  2  3  3 即 f x+ = f −x+ ，即 f (3+x)= f (−x).  2  2 因为 f (−x )=−f ( x ) ，所以 f (3+x)=−f (x)=−f (3−x)，故C正确； 因为 f (3+x)=−f (x)，所以 f (x+6)=−f (x+3)= f (x)，所以 f ( x ) 的周期为6. 3 因为 f (3+x)= f (−x)，所以 f ( x ) 的对称轴为x= ， 2 因为 f(1)= 3，所以 f (2)= f (1)= 3， f (3)= f (0)=0， f (4)= f (−1)=−f (1)=− 3， f (5)= f (5−6)= f (−1)=− 3， f (6)= f (0)=0， 所以 f (1)+ f (2)+ f (3)+ f (4)+ f (5)+ f (6) = 3+ 3+0− 3− 3+0=0. 又2023=6×337+1， 2023 所以∑ f(k)=337× f (1)+ f (2)+ f (3)+ f (4)+ f (5)+ f (6)  + f (1)= 3，故D正确. k=1 故选ACD. 12. 【分析】 第12页，共16页 学科网（北京）股份有限公司本题考查集合的新定义问题，属于基础题. 根据A B的定义即可求出集合中的元素，从而得出各元素之和． 【解答】 解：当x=0,y=2,∴z=0； 当x=1,y=2,∴z=6； 当x=0,y=3,∴z=0； 当x=1,y=3,∴z=12， ∴集合A B={0,6,12}， ∴集合A B所有元素的和为0+6+12=18. 故答案为：18. 13. 【分析】 本题考查双曲线的简单性质，以及几何体体积的计算，属于中档题. 过y轴任意一点作直线l //BC ，交双曲线渐近线、双曲线于B′、C′，计算内部圆形(绿色部分)和环带 面积(橙色部分)，利用祖暅原理即可求解. 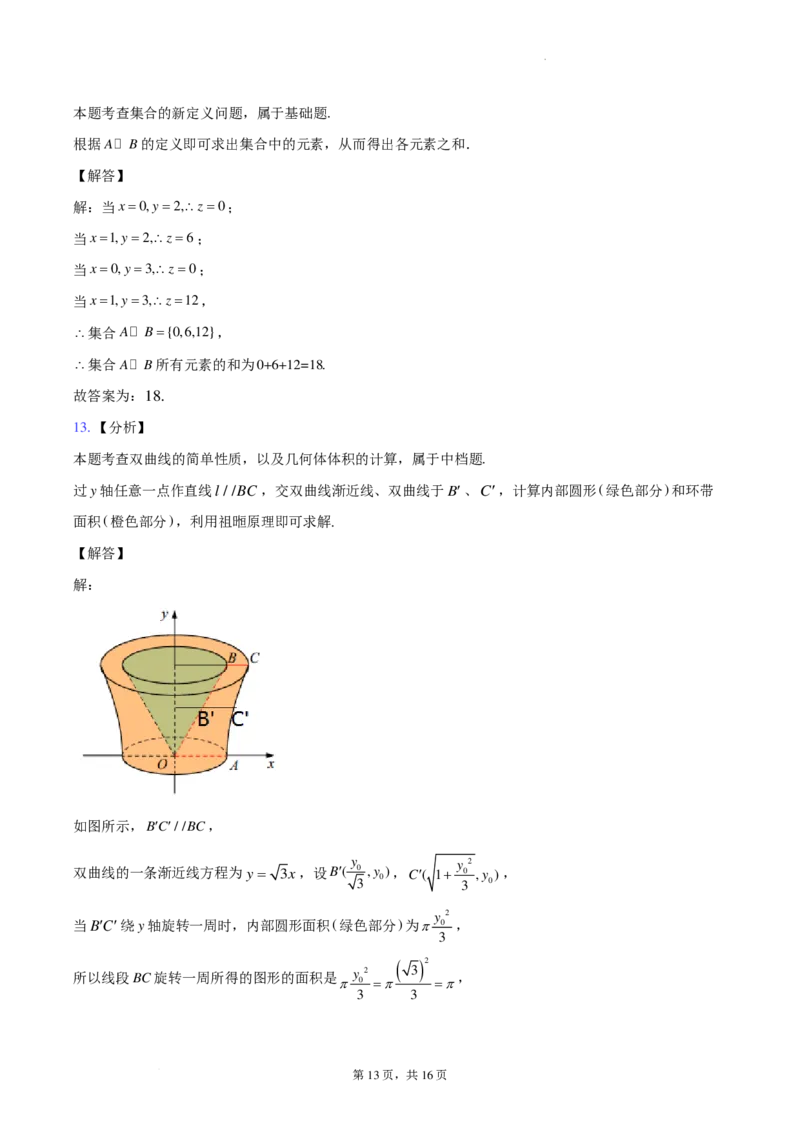【解答】 解： 如图所示，B′C′//BC， y y 2 双曲线的一条渐近线方程为 y = 3x，设B′( 0 ,y )，C′( 1+ 0 ,y )， 3 0 3 0 y 2 当B′C′绕y轴旋转一周时，内部圆形面积(绿色部分)为π 0 ， 3 ( )2 所以线段BC旋转一周所得的图形的面积是 π y 0 2 =π 3 =π ， 3 3 第13页，共16页 学科网（北京）股份有限公司2  y 2  y 2 外部橙色环带面积为π 1+ 0  −π 0 =π，  3  3   此部分对应的体积等价于底面积为π，高为 3的圆柱， 1 4 3 所以几何体Γ的体积为π 3(橙色部分)+ π 3(圆锥部分)= π. 3 3 4 3 故答案为 π； π. 3 14. 【分析】 本题考查集合的新定义，为难题. 【解答】 解：7阶中元素个数为7个，设为{1,2,3,4,5,6,7}，则7阶的三元子集的集合个数为C3 =35， 7 若要使得X中的任意两个不同的元素，都恰好同时包含在唯一的一个三元子集中， { } 不妨先挑选 1,2,3 ，则三元子集中不能包含： {1,2,4},{1,2,5},{1,2,6},{1,2,7},{2,3,4},{2,3,5},{2,3,6},{2,3,7}{1,3,4},{1,3,5},{1,3,6},{1,3,7}，共12个剔除； 再从剩余三元子集中挑选{1,4,5}，则剩余三元子集中不能包含： {1,4,6},{1,4,7},{1,5,6},{1,5,7},{2,4,5},{3,4,5},{4,5,6},{4,5,7}，共8个剔除； 接着再在剩余三元子集中挑选{1,6,7}，则此时剩余三元子集中不能包含： {2,6,7},{3,6,7},{4,6,7},{5,6,7}，共4个剔除; 接着再在剩余三元子集中挑选{2,4,6}，则此时剩余三元子集中不能包含： {2,4,7},{3,4,6},{4,5,6}共3个剔除， 接着再在剩余三元子集中挑选{2,5,7}，则此时剩余三元子集中不能包含： {3,5,7}，共1个剔除； 综上一共剔除28个，此时剩余{3,4,7},{3,5,6}，均符合题意. 则集合A中元素的个数为7. 第14页，共16页 学科网（北京）股份有限公司15. 本题考查导数知识的运用，考查函数的极值，考查函数的单调性，正确求导，合理分类是关键． (1)确定函数的定义域，求导函数，利用x=1是函数 y = f(x)的极值点，即可求a的值； (2)分类讨论，利用导数的正负，结合函数的定义域，可得函数的单调区间． 16. 本题考查相互独立事件的概率，以及离散型变量的分布列与均值，属于中档题. (1)根据相互独立事件的概率公式即可求解； (2)列出X的所有可能取值，根据相互独立事件的概率公式分布求解对应的概率从而可得分布列，再利用 期望公式求解即可. 17. (1)利用面面垂直的性质定理可得出AC ⊥平面PBD，再利用线面垂直的性质可证得AC ⊥ PB. (2)设 AC∩BD=O，推导出PO⊥平面ABCD，可得出∠PAO为PA与平面ABCD所成角，然后以点O 为坐标原点，OA、OB、OP所在直线分别为x、y、z轴建立空间直角坐标系，利用空间向量法可求得平面 EBD与平面BCD的夹角的余弦值． 本题考查直线与平面的位置关系，二面角，解题关键是空间向量法的应用，属于中档题． 18. 本题考查了椭圆的方程，直线与椭圆的位置关系，方程思想，转化思想，考查了运算能力，属于难题. 3 (Ⅰ)由离心率为 ，|FF |=2 3，列式计算a，b，即可得椭圆C的方程的方程. 2 1 2 m m  m x2 (Ⅱ)直线PA ，PA 的方程分别为：y= (x+2)， y = (x−2)，由y= (x+2) + y2 =1得 1 1 6 2  6 4 18−2m2 m 6m (9+m2)x2 +4m2x+4m2 −36=0，可得x = ，y = (x +2)= ，同理可得 M 9+m2 M 6 M 9+m2 2m2 −2 m −2m −2m 2m 2m2 −2 x = ，y = (x −2)= ，直线MN的方程为：y− = (x− )， N 1+m2 N 2 N 1+m2 1+m2 3−m2 1+m2 2m 2m2 −2 2m 2m 2m2 −2 3−m2 2m y= (x− )− = (x− − )= (x−1)，可得直线MN过定点(1,0)， 3−m2 1+m2 1+m2 3−m2 1+m2 1+m2 3−m2 故设MN的方程为：x=ty+1， 由  x=ty+2 x2 + y2 =1得(t2 +4)y2 +2ty−3=0，| y − y |= (y + y )2 −4y y = 4 t2 +3 ，即OMN 的面  4 1 2 1 2 1 2 t2 +4 1 t2 +3 积S = ×1×(y − y )=2 利用函数单调性即可求出面积最大值． 2 1 2 t2 +4 19. 本题考查数阵新定义问题，属于综合题. (1)根据题中条件可判断结果，根据题中公式进行计算即可； (2)根据条件讨论 a 的值，根据 d(a ,a )=|a −a |+|a −a | ，得到相关的值， i+1,j i,j s,t i,j s,j s,j s,t 第15页，共16页 学科网（北京）股份有限公司进行最小值求和即可； (3)当 r2 时，将横向相邻两个 k 用从左向右的有向线段连接，则该行有 r −1 条有向线段，得到横向有 i i 向线段的起点总数，同样的方法得到纵向有向线段的起点总数，根据条件建立不等关系，即可证明. 第16页，共16页 学科网（北京）股份有限公司