梅州市高三第一次质检（2024.2）数学参考答案与评分标准(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_2024届梅州2月质检数学试题+答案

梅州市高三第一次质检（2024.2） 数学参考答案与评分意见 一、选择题：本题共 8 小题，每小题 5分，共 40 分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 1 2 3 4 5 6 7 8 D C C B A D A C 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合 题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 9 10 11 BCD BCD ABC 三、填空题：本题共3小题，每小题5分，共15分。 1 1 10 105 12. 7 13. 10n1  n 14. [ ,2 5) 27 3 27 3 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15.（本小题满分13分） 解：（1）因为 a 为等差数列，设其公差为d ； b 为等比数列，设其公比为q， n n  b a  4 1 1  依题意有： bq a d 1 ， .......................2分 1 1  bq2 2(a 2d)4 1 1 4q 5d 得到： ， .......................3分 q2 1d q 2 解得： ， .......................4分 d 3 因此a 43(n1)3n1， .......................5分 n b 42n1 2n1. .......................6分 n（2） 因为a 3441133，又b 27 128a ，b 256a ， ........8分 44 6 44 7 44 且等差数列 a 3n1 和等比数列  b 2n1  均为单调递增数列， .............9分 n n 所以数列 c 的前50项包含 a 的前44项和 b 的前6项， .............10分 n n n 数列 c 的前50项和S a a ......a b b b b b b ......11分 n 50 1 2 44 1 2 3 4 5 6 44(4133) 4(126)   .......................12分 2 12 3266. .......................13分 16.（本小题满分15分） 解：（1）由已知可得，甲赢得比赛的情况有以下三种： 3 2 8 ① 情况一：比赛三局且甲均获胜，其概率为P     ， ..................2分 1 3 27 ② 情况二：比赛四局，甲前三局胜两局，输一局，第四局甲获胜， 2 2  2 2 8 其的概率为：P C2    1    ， .......................4分 2 3 3  3 3 27 ③ 情况三：比赛五局，甲前四局胜两局，输两局，第五局甲获胜， 2 2 2  2 2 16 其概率为P C2    1    ， .......................6分 3 4 3  3 3 81 8 8 16 64 综上，甲获胜的概率为P  P P P     . ................8分 1 2 3 27 27 81 81 （2）设两人比赛局数为X ，则随机变量X 的可能取值为3,4,5， ...................9分 3 3 2 1 1 P(X 3)       ， .......................10分 3 3 3 2 2 2 1 2 1 2 1 8 2 10 P(X 4)C2     C2        ， .......11分 3 3 3 3 3 3 3 3 27 27 27 1 10 8 P(X 5)1P(X 3)P(X 4)1   ， .......12分 3 27 27 1 10 8 107 则随机变量X 的数学期望E(X)3 4 5  . 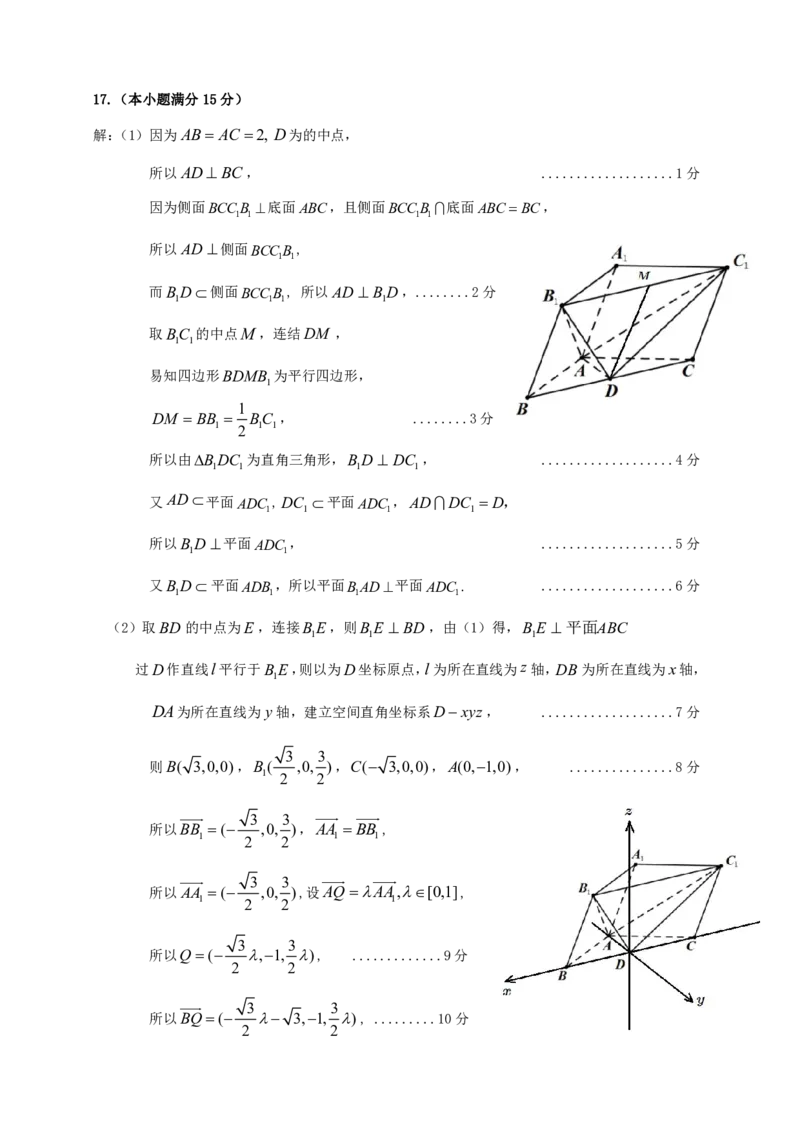.......15分 3 27 27 2717.（本小题满分15分） 解：（1）因为AB AC 2, D为的中点， 所以ADBC， ...................1分 因为侧面BCCB 底面ABC，且侧面BCCB 底面ABCBC， 1 1 1 1 所以AD 侧面BCCB , 1 1 而BD 侧面BCCB , 所以AD  BD，........2分 1 1 1 1 取BC 的中点M，连结DM ， 1 1 易知四边形BDMB 为平行四边形， 1 1 DM  BB  BC ， ........3分 1 2 1 1 所以由BDC 为直角三角形，BD  DC ， ...................4分 1 1 1 1 又AD平面ADC ,DC 平面ADC ，ADDC  D， 1 1 1 1 所以BD 平面ADC ， ...................5分 1 1 又BD 平面ADB ，所以平面BAD平面ADC . ...................6分 1 1 1 1 （2）取BD 的中点为E，连接BE，则BE  BD，由（1）得，BE 平面ABC 1 1 1 过D作直线l平行于BE，则以为D坐标原点，l为所在直线为z轴，DB为所在直线为x轴， 1 DA为所在直线为 y轴，建立空间直角坐标系Dxyz， ...................7分 3 3 则B( 3,0,0)，B ( ,0, )，C( 3,0,0)，A(0,1,0)， ...............8分 1 2 2  3 3   所以BB ( ,0, )，AA  BB , 1 2 2 1 1  3 3   所以AA ( ,0, ),设AQ AA,[0,1], 1 2 2 1 3 3 所以Q ( ,1, ), .............9分 2 2  3 3 所以BQ (  3,1, ), .........10分 2 2 又设平面ACC A 的法向量为n(x,y,z), 1 1     3x y 0  nAC 0  因为  ，即  3 3 , ...................11分 nAA 0  x z 0 1  2 2 令x  3，则 y 3,z 1,  所以n( 3,3,1), ...................12分 3 3 (  3) 33    3 所以sin600  cos BQ,n  2 2  .............13分 ， 2 3 3 (  3)21( )2 2 2 整理得：392 3940， 而显然当01时，392 3940， 392 3940在区间[0,1]上无解， ...................14分 即在棱AA 上不存在满足题意的点Q. ...................15分 1 18.（本小题满分17分） ax 解：（1）因为 f(x)ln(x1) (a0)， x1 x1a 所以 f(x) (a0)， ...................1分 (x1)2 因为x1是函数 f(x)的一个极值点， 故 f'(1)0，即a2， ...................2分 当a2时，代入检验，x1确是函数 f(x)的一个极小值点， ...................3分 所以a2． ...................4分 （2）因为 f(x)0在[0,)上恒成立，所以 f (x)  0． ...................5分 min x1a 当0a1时， f(x) 0在[0,)上恒成立， (x1)2 即 f(x)在[0,)上为增函数， ...................6分 所以 f(x)  f(0)0成立，即0a1满足题意． ...................7分 min x1a 当a1时，令 f(x) 0，得xa1， (x1)2x1a 令 f(x) 0，得0 xa1， ...................8分 (x1)2 即 f(x)在(0,a1)上为减函数，在(a 1,) 上为增函数． ...................9分 当x(0, a1)时， f(x) f(0)0，这与 f(x)0矛盾． ...................10分 综上所述，a 的取值范围是(0,1]． ...................11分 2024 （3）证明：要证( )2024 e， 2023 2024 2024 1 两边取自然对数得，2024ln 1，等价于：ln  ， .............12分 2023 2023 2024 2024 1 只需证：ln  0， ...................13分 2023 2024 x 由（2）知，当a1时， f(x)ln(x1) 在(0,)单调递增． .............14分 x1 1 f( 1 )ln(1 1 ) 2023 ln 2024  1  f(0)0 ， ...................16分 2023 2023 1 2023 2024 1 2023 从而原命题成立． ...................17分 19.（本小题满分17分） 解：（1）因为ON 1，所以点N的轨迹是以原点O为圆心，半径为1的圆， ............1分 于是曲线C 的轨迹方程为x2  y2 1. ...................2分 1 设M  x,y  ,N  x ,y  ,D  t,0  , t 2. 0 0     由题可知,MD  DN , ON  DN 1,  tx,y  x t,y  x2tx   0 0  0 所以x2  y2 1 ,即y y . ...................3分 0 0 0     x 0 t 2  y 0 2 1  t  t2x 0 0 由于t不恒为0，所以t 2x ， 0  x x  故 0 3 . ...................4分  y y 0 1  x 2 x2 又x2  y2  ，所以  y 2 1，即  y2 1, ...................5分 0 0 4 3 9 x2 故曲线C 的轨迹方程为  y2 1. ...................6分 2 9（2）易知E1,0，F1,0， ...................7分 设P  x ,y  ,Q  x ,y  , 1 1 2 2 km 则点E到直线l: y  kxm的距离为d  ， 1 k2 1 k m 点F 到直线l: y  kxm的距离为d  . ...................8分 2 k2 1 m 因为l与C 相切，所以 1，即m2 k2 1， ...................9分 1 k2 1 x2   y2 1 由9 ，  y kxm   得 19k2 x2 18kmx9(m2 1)0， ...................10分    36 9k2m21   18km 所以x x  ， ...................11分 1 2 19k2   9(m2 1) x x   1 2 19k2 6 1k2 9k2 m2 1 故 PQ  1k2 x x  . ...................12分 1 2 19k2 又m2 k2 1，由36  9k2 m2 1  368k2 0，得k 0， .......13分 1 1 9  m2 k2 9k2 m2 1  所以S S   PQ d   PQ d  . EPQ FPQ 2 1 2 2  19k22 72k2 72k2 72 所以S S    ， .......14分 EPQ FPQ  19k22 118k2 81k4 1 1881k2 k2 1 而 81k2182 811836 ， ...................15分 k2 72 则S S  (0,2]. ...................16分 EPQ FPQ 1 1881k2 k2 因此S S 的取值范围为 0,2  . ...................17分 EPQ FPQ