柳州高中、南宁三中2024届一轮复习诊断性联考数学解析版_2024年2月_01每日更新_24号_2024届广西邕衡金卷柳州高中、南宁三中高三一轮复习诊断性联考

柳州高中、南宁三中2024届一轮复习诊断性联考 数学 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡 皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。 3．考试结束后，将本试卷和答题卡一并交回。 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题 目要求的． 1.已知集合A=1,3,4  ，集合B=2,3,4,6  ，则如图中的阴影部分表示( ) A. 3,4  B. 1  C. 2,6  D. 1,2,3,4,6  【答案】C 【详解】因为韦恩图中的阴影部分表示的是属于B不属于A的元素组成的集合，又A=1,3,4  ，B=2,3,4,6  ，所 以韦恩图中的阴影部分表示的集合是2,6  . 故选：C. 2.已知命题p：∃x∈R,lgx+x≥3，则¬p为 ( ) A.∀x∈R,lgx+x<3 B.∃x∈R,lgx+x<3 C.∀x∈R,lgx+x≥3 D.∃x∈R,lgx+x≤3 【答案】A 【详解】命题p是存在量词命题，所以¬p是“∀x∈R,lgx+x<3”。故选A. 3.一组数据从小到大的顺序排列如下：9,10,12,15,17,18,22,26经计算，则75%分位数是( ） A.18 B.20 C.21 D.22 【答案】B 18+22 【解析】因为8×75%=6,故75%分位数是第6个和第7个的平均数，则 =20 2 π 4.若cosα+ 4  3 = ，则sin2α= ( ) 5 7 7 9 9 A. B.- C. D.- 25 25 25 25 【答案】A π 【详解】cos2α+ 4  π =cos2α+ 4  π -sin2α+ 4  3 = 5  2 4 - 5  2 7 π =- ,所以sin2α=-cos2α+ 25 2  7 = . 25 故选：A 5.已知f(x)= cosx 为奇函数，则a= ( ) (x2+3x)(x+a) A.3 B.-3 C.0 D.-1 【答案】B 【详解】由（x2+3x)(x+a)≠0⇒x≠0且x≠-3且x≠-a.因为该函数为奇函数，所以定义域关于原点对称，因此 -a=3⇒a=-3,即f(x)= cosx = cosx = cosx .因为f(-x)= cos(-x) =- cosx =-f(x), (x2+3x)(x-3) x(x+3)(x-3) x(x2-9) -x(x2-9) x(x2-9) {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}所以该函数是奇函数，符合题意。 故选B. 6. 抛物线有如下光学性质：平行于抛物线对称轴的光线，经过抛物线上的一点反射后，反射光线经过抛物线的焦点． 过点P2 2,5  且平行于y轴的一条光线射向抛物线C：x2=4y上的A点，经过反射后的反射光线与C相交于点 B，则AB  =( ) 7 9 A. B.9 C.36 D. 2 2 【答案】D 【详解】解：由题意得点A的坐标为2 2,2  ，C的焦点为F0,1  2 ，所以直线AB的方程为y= x+1，与抛物线 4 2 方程x2=4y联立，消去y得x2- 2x-4=0，由韦达定理得x +x = 2，所以y +y = x +x A B A B 4 A B  5 +2= ， 2 所以由抛物线的定义得AB  9 =y +y +2= ．故选：D A B 2 7. 如果一个数列从第2项起，每一项与它前一项的和除以与它前一项的差等于同一个常数，那么这个数列就叫做 “和差等比数列”.已知a n  是“和差等比数列”，a =1，a =3，则满足使不等式a >100的n的最小值是( ) 1 2 n A.8 B.7 C.6 D.5 【答案】C a +a a +a a 【详解】依题意， n+1 n = 2 1 =2，得 n+1 =3，则数列a a -a a -a a n n+1 n 2 1 n  是首项为1，公比为3的等比数列，所以a =1⋅ n 3  n-1=3n-1，检验知，当n≥6时，36-1=243>100成立，所以n的最小值是6. 故选：C. 8.某同学参加学校组织的数学知识竞赛，在5道四选一的单选题中有3道有思路，有2道完全没有思路，有思路的题 1 目每道做对的概率为 ，没有思路的题目只好任意猜一个答案.若从这5道题目中任选2题，则该同学2道题目都 2 做对的概率为( ） 1 7 3 5 A. B. C. D. 4 32 16 32 【答案】D 1 1 【详解】若该同学从中选到2道有思路的，则都做对的概率为( )2= ， 2 4 1 1 1 若该同学从中选到 1道有思路的和1道完全没有思路的，则都做对的概率为 × = , 2 4 8 1 1 若该同学从中选到2道完全没有思路的，则都做对的概率为( )2= 4 16 所以由全概率公式，若从这5道题目中任选2题，则该同学2道题目都做对的概率为 C2 1 C1C1 1 C2 1 3 1 6 1 1 1 3 3 1 25 5 3 × + 3 2 × + 2 × = × + × + × = + + = = C2 4 C2 8 C2 16 10 4 10 8 10 16 40 40 160 160 32 5 5 5 故选：D. 二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求． 全部选对的得6分，部分选对的得部分分，有选错的得0分． 9. 若复数z满足zi=1-i,则下列命题正确的有( ) A.z的虚部是-1 B. z  = 2 C.z2=2 D.z是方程x2+2x+2=0的一个根 【答案】ABD 【详解】zi=1-i⇒z=-1-i，故A,B正确 ; z2=(-1-i)2=2i ，故C错误;而(-1-i)2+2(-1-i)+2=0成立， 故D正确。故选：ABD 10. 在物理学中，把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”．在适 当的直角坐标系下，某个简谐运动可以用函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示，则 {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}下列结论正确的是( ) 1 π A.ω=2,频率为 ，初相为 π 6 π B.函数f(x)的图象关于直线x=- 对称 6 π 13π C.函数f(x)在[ , ]上的值域为[0,2] 12 24 2 D.若把f(x)图像上所有点的横坐标缩短为原来的 倍，纵坐标不 3 π π 变，再向左平移 个单位，则所得函数是y=2sin3x+ 12 12  【答案】BCD 3 13π π 3π 1 1 2π π π 【详解】由图象可得A=2, T= - = ，∴T=π，频率是 = ，ω= =2，∵f( )=2，∴f( )= 4 12 3 4 T π π 3 3 2π 2sin +φ 3  2π =2，即sin +φ 3  2π π π =1，∴ +φ=2kπ+ (k∈Z)，∴φ=2kπ- (k∈Z)，∵|φ|<π，∴φ= 3 2 6 π - ， 6 π ∴f(x)=2sin2x- 6  π ，初相是- ,故A错误； 6 π π π f(- )=2sin- - 6 3 6  =-2,故B正确； π 13π π 11π 因为x∈[ , ],所以2x- ∈ 0, 12 24 6  12  π ∴f(x)=2sin2x- 6  π 13π 在[ , ]上的值域为[0,2]，故C正确； 12 24 2 π 把f(x)的横坐标缩短为原来的 倍，纵坐标不变，得到的函数为y=2sin3x- 3 6  π ，又向左平移 个单位，得到 12 π 的函数为y=2sin 3x+ 12  π   -  6  π =2sin(3x+ )，故D正确； 12 故选：BCD     11.在边长为2的正方体ABCD-A B C D 中，动点M满足AM =xAB+yAD+zAA ,(x,y,z∈R且x≥0,y≥0,z 1 1 1 1 1 ≥0)，下列说法正确的是( ) 1 A.当x= ,z=0,y∈[0,1]时，BM+MD的最小值为 13 4 1 1 10 B.当x=y=1,z= 时，异面直线BM与CD 所成角的余弦值为 2 1 5 2 5 4 2π C.当x+y+z=1，且AM= 时，则M的轨迹长度为 3 3 6 D.当x+y=1,z=0时，AM与平面ABD 所成角的正弦值的最大值为 1 1 3 【答案】AD      1 1 【详解】对于A，在AB上取点H，使AH= AB，在DC上取点K，使DK= DC，因为AM = 4 4   1 xAB+yAD，x= ，y∈0,1 4  ，所以M点在线段HK上，将平面BHKC 与平面AHKD沿着 1 1 HK展开到同一平面内，如图1所述，连接BD，交于HK于点P，此时B,P,D三点共线，BP+ 1 1 1 3 PD取得最小值，由勾股定理得BH= 22+ 1 2  2 = 5 ，则AB = 5 + 1 =3，BD= 22+32 2 1 2 2 1 = 13，所以A正确。 1 对于B，因为x=y=1,z= ，所以M为CC 的中点，连接BM，取CD 中点N，连接MN,BN, 2 1 1 1 所以∠BMN为异面直线BM与CD 所成角(或其补角)，易得MN= 2,BM= 5,BN=3,所以由余弦定理得： 1 ( 5)2+( 2)2-32 10 cos∠BMN= =- ,所以异面直线BM与CD 所成角的余弦 2 5⋅ 2 10 1 10 值为 ，所以B错误。 10 对于C，当x+y+z=1时，可得点M的轨迹在△ABD内(包括边界)．易知AC ⊥ 1 1 4 平面ABD，设AC 与平面ABD相交于点P．由于V =V = ，则点A 1 1 1 A-A1BD A1-ABD 3 {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}4 3 2 3 2 5 2 2 到平面ABD的距离为AP= = ．若AM= ，则MP= ，即点M的轨迹是以P 1 1 3 3 3 3 × ×(2 2)2 3 4 2 2 6 2 2 为圆心， 为半径的圆，如图所示，法一：圆心P到△A EP三边距离为 < ,故M的轨迹是以P为圆 3 1 3 3 2 2 4 2π 2 6 心， 为半径的圆的一部分，轨迹长度比小于圆周长 ,故C错误．法二：在△A EP中，AP= ，PE 3 3 1 1 3 2 2 π 8 2 6 3 8 2 2 = ,∠EAP= ，设A E=x>0，由余弦定理得x2+ -2x⋅ ⋅ = ，解得A E= =PE，则 3 1 6 1 3 3 2 9 1 3 π π 2 2 2 2π ∠APE=∠EAP= ，所以M的轨迹长度为 ×6× = ，故C错误． 1 1 6 6 3 3 对于D，因为BD ⎳BD，BD⎳平面ABD ，因为M∈BD，点M到平面ABD 的距离等于点B到平面ABD 的 1 1 1 1 1 1 1 1 1 1 1 4 距离，设点B到平面ABD 的距离d，则V =V ，V = S ⋅AD = × ×2×2×2= 易 1 1 B-AB1D1 D1-ABB1 D1-ABB1 3 △ABB1 1 1 3 2 3 3 知△AB 1 D 1 是边长为2 2的等边三角形，则S △AB1D1 = 4 ×2 2  2=2 3，    1 1 4 2 3 由V = S ⋅d= ×2 3d= ，解得d= ，因为AM =xAB+yAD,x+y=1，所以M在线段 B-AB1D1 3 △AB1D1 3 3 3 BD上运动，则当点M为线段BD的中点时，AM取最小值 2，设直线AM与平面ABD 所成角为θ，则sinθ= 1 1 2 3 2 3 d 3 3 6 = ≤ = ，D对. AM AM 2 3 故选：AD. 三、填空题：本题共3小题，每小题5分，共15分．  12.已知向量a=1,m   ,b=3,-1    .若2a-b    ⎳a+2b  ，则实数m的值为 . 1 【答案】- 3  【详解】因为a=1,m   ,b=3,-1    ，所以2a-b=-1,2m+1    ,a+2b=7,m-2    .又2a-b    ⎳a+2b  ，所以 -m-2  -72m+1  1 1 =0，解得m=- .故答案为：- . 3 3 1 13.已知ax+ x  5 1 2x- x  (a为常数)的展开式中所有项的系数和为32，则展开式中x2的系数为 (用数 字作答) 【答案】15 【详解】令x=1，则a+1  1 5=32，即a=1，则对x+ x  5 ，有T =Ckx5-k 1 k+1 5 x  k =Ckx5-2k，令5-2k=1，即k=2， 5 1 有T =C2⋅x=10x，即有T ×2x=20x2，令5-2k=3,即k=1，有T =C1⋅x3=5x3，即有T ×- 3 5 3 2 5 2 x  =-5x2,故展 开式中x2的系数为15 14.已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，⋯，其中第一项是20，接下来的两项是20，21，再接下来的三项 是20，21，22，依此类推，若该数列的前n项和为S ,若log (S )∈Z,n∈N*,则称(n,log (S ))为“好数对”，如 n 2 n 2 n log (S )=log 20=0，log (S )=log 21=1,则(1,0),(2,1)都是“好数对”，当n≥66时，第一次出现的“好数对”是 2 1 2 2 2 2 . 【答案】(95,14) 【详解】若log (S )∈Z,则S 为2的整数幂，将数列排成如下的形式 2 n n 1 1，2 1，2，4 1，2，4，8 1×(1-2k) 第k行为：20，21，⋯，2k-1，第k行和为 =2k-1， 1-2 {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}k(k+1) 该数列前1+2+3+⋯+k= 项的和为S =(21-1)+(22-1)+⋯+(2k-1)=2k+1-k-2 2 k(k+1) 2 k(k+1) 令 ≥66,∴k≥11,此时k+2<2k+1,∴k+2是第k+1行的部分项之和，即k+2=1+2+⋯+2t=2t-1 2 (1+13)×13 则k=2t-3≥11,∴t≥4,此时k=24-3=13,所以n的最小值为 +4=95,此时S =214, 2 95 log (S )=14,∴当n≥66时，第一次出现的“好数对”是(95,14) 2 95 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． a-b sinA-sinC 15.（13分）记△ABC的内角A,B,C的对边分别为a,b,c，已知 = ． c sinA+sinB (1)求角B的大小； (2)若b=2，求△ABC周长的最大值． π 【答案】(1)B= ；(2)6 3 a-b sinA-sinC a-b a-c 【详解】(1)根据 = 及正弦定理，得 = ，2分 c sinA+sinB c a+b 得a2+c2-b2=ac， a2+c2-b2 ac 1 根据余弦定理，得cosB= = = ，4分 2ac 2ac 2 又B∈0,π  π ，所以B= ．6分 3 (2)由余弦定理得b2=a2+c2-2accosB=4,8分 a+c 由基本不等式得(a+c)2=4+3ac≤4+3( )2,10分 2 所以a+c≤4,当且仅当a=c=2时取等。12分 所以△ABC周长的最大值为6.13分 a b c 4 法二：由正弦定理 = = = 8分 sinA sinB sinC 3 4 4 π 4 3 3 3 1 得a+c= (sinA+sinC)= [sinA+sin(A+ )]= ( sinA+ cosA)=4( sinA+ cosA) 3 3 3 3 2 2 2 2 π =4sin(A+ )≤4，11分 6 π 当且仅当A= 时等号成立.12分 3 故△ABC周长的最大值为6.13分 16.（15分）某校为了丰富学生课余生活，体育节组织定点投篮比赛.为了解学生喜欢篮球是否与性别有关，随机抽取 了男、女同学各100名进行调查，部分数据如表所示： 喜欢篮球 不喜欢篮球 合计 男生 40 女生 30 合计 (1)根据所给数据完成上表，依据小概率值α=0.001的χ2独立性检验，能否据此推断该校学生喜欢篮球与性别有 关？ (2)篮球指导老师从喜欢篮球的学生中抽取了2名男生和1名女生进行投篮示范.已知这两名男生投进的概率均 3 2 为 ，这名女生投进的概率为 ，每人投篮一次，假设各人投篮相互独立，求3人投进总次数X的分布列和数学期 4 3 望. nad-bc 附：χ2=  2 a+b  c+d  a+c  b+d  α 0.1 0.05 0.01 0.005 0.001 {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}x 2.706 3.841 6.635 7.879 10.828 α 13 【答案】(1)见解析；(2)分布列见解析，数学期望为 . 6 【详解】(1)依题意，2×2列联表如下： 喜欢篮球 不喜欢篮球 合计 男生 60 40 100 女生 30 70 100 合计 90 110 200 2分 零假设H ：该校学生喜欢篮球与性别无关， 0 200(60×70-30×40)2 200 χ2= = ≈18.182>10.828=x ，6分 100×100×90×110 11 0.001 根据小概率值α=0.001的独立性检验，推断H 不成立，即认为该校学生喜欢篮球与性别有关。7分 0 (2)依题意，X的可能值为0,1,2,3，8分 3 P(X=0)=1- 4  2 2 ×1- 3  1 = ，9分 48 3 3 P(X=1)=C1× 1- 2 4 4  2 ×1- 3  3 +1- 4  2 2 1 × = ，10分 3 6 3 3 P(X=2)=C1× 1- 2 4 4  2 3 × + 3 4  2 2 ×1- 3  7 = ，11分 16 3 P(X=3)= 4  2 2 3 × = ，12分 3 8 所以X的分布列为： X 0 1 2 3 1 1 7 3 P 48 6 16 8 1 1 7 3 13 数学期望E(X)=0× +1× +2× +3× = .15分 48 6 16 8 6 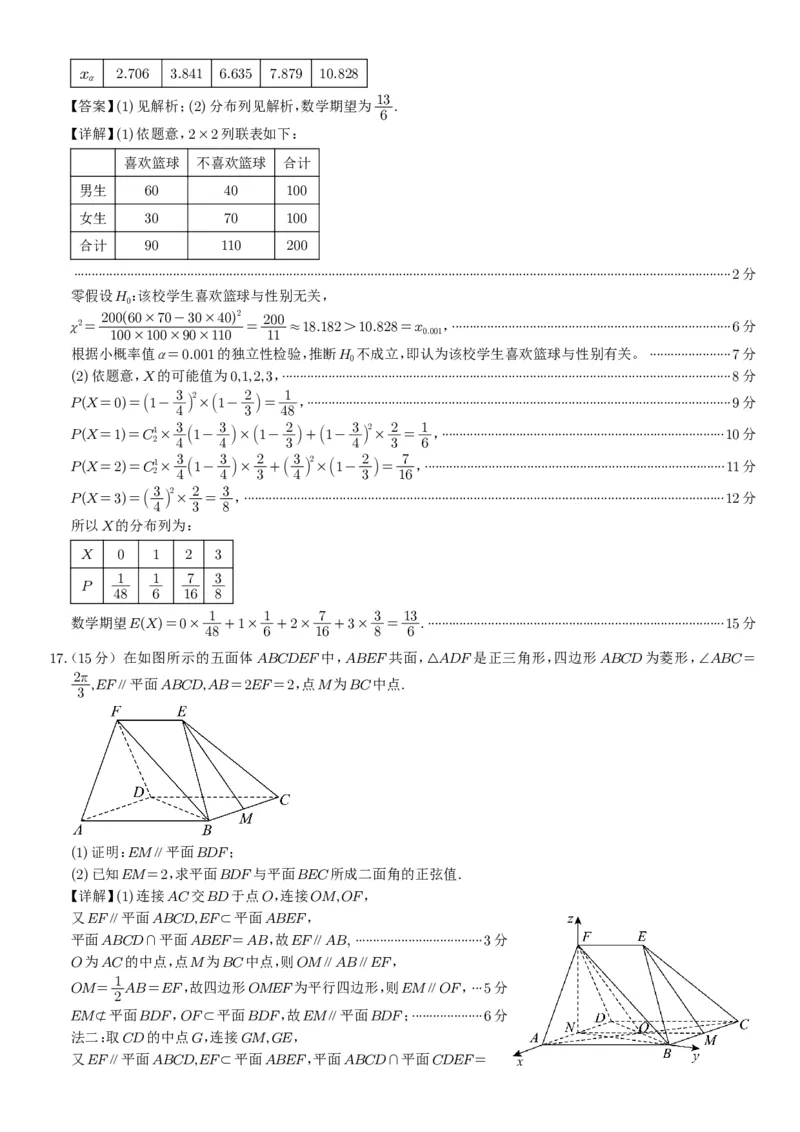17.（15分）在如图所示的五面体ABCDEF中，ABEF共面，△ADF是正三角形，四边形ABCD为菱形，∠ABC= 2π ,EF∥平面ABCD,AB=2EF=2，点M为BC中点. 3 (1)证明：EM∥平面BDF； (2)已知EM=2，求平面BDF与平面BEC所成二面角的正弦值. 【详解】(1)连接AC交BD于点O，连接OM,OF， 又EF∥平面ABCD,EF⊂平面ABEF， 平面ABCD∩平面ABEF=AB，故EF∥AB, 3分 O为AC的中点，点M为BC中点，则OM∥AB∥EF， 1 OM= AB=EF，故四边形OMEF为平行四边形，则EM∥OF，5分 2 EM⊄平面BDF，OF⊂平面BDF，故EM∥平面BDF；6分 法二：取CD的中点G，连接GM,GE， 又EF∥平面ABCD,EF⊂平面ABEF，平面ABCD∩平面CDEF= {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}CD，故CD∥EF.3分 又G为CD的中点，则DG⋕EF,故四边形DGEF为平行四边形,则DF∥GE, GE⊄平面BDF,DF⊂平面BDF,故EG∥平面BDF； 点M为BC中点，则GM∥BD,GM⊄平面BDF,BD⊂平面BDF,故GM∥平面 BDF； EG∩GM=M,EG,GM⊂平面EMG，故平面EMG∥平面BDF 5分 又EM⊂面EMG,∴EM∥平面BDF 6分 (2)由(1)可知，OF=EM=2，取AD中点N，连接FN,ON,BN，在△ONF中，FN= 3,ON=1,OF=2，则FN2 +ON2=OF2， 所以ON⊥FN， 因为△ADF是正三角形，所以AD⊥FN，又AD∩ON=N,AD,ON⊂平面ABCD，则FN⊥平面ABCD， BN⊂平面ABCD，故FN⊥BN； 因为△ABD是正三角形，所以BN⊥AD，因为AD∩FN=N,AD,FN⊂平面ADF，所以BN⊥平面ADF， 以N为原点，分别以NA,NB,NF所在直线为x,y,z轴建立如图所示的空间直角坐标系N-xyz，8分 1 3 则A(1,0,0),B(0, 3,0),C(-2, 3,0),E- , , 3 2 2  ，F(0,0, 3),D(-1,0,0),   3 3 则CB=(2,0,0),CE= ,- , 3 2 2   ,AB=(-1, 3,0)，9分  设平面BEC的法向量为m=(x,y,z)，   2x=0 m⋅CB=0   则  ，即 3 3 ，令z=1，则y=2，故m=(0,2,1)，11分 m⋅CE=0 x- y+ 3z=0 2 2    BD=(-1,- 3,0),DF=(1,0, 3),设平面BDF的法向量为n=(a,b,c)，   则   n  ⋅B  D  =0 ，即  -a- 3b=0 ，令a= 3，得平面BDF的法向量n  = 3,-1,-1 n⋅DF=0 a+ 3c=0  ，13分     m⋅n -2-1 3 故cos‹m,n›= |m  ||n  | = 5⋅ 5 =- 5 ，由于平面BDF与平面BEC所成二面角为θ∈0,π  ，则cosθ  3 = ，所以 5 4 平面BDF与平面BEC所成二面角的正弦值为sinθ= 1-cos2θ= .15分 5 18.（17分）已知函数fx  =lnx-ax+a,g(x)=x-1  ex-a-ax+1a∈R  . (1)若fx  ≤0,求a的值； (2)当a∈0,1  时，证明：g(x)≥fx  . 【答案】(1)a=1;(2)见详解。 【详解】(1)法一;∵f1  =0，∴fx  ≤0=f1  1分 ∴0是f(x)的最大值点，故也是f(x)的极大值点，f'(1)=03分 1 又f'(x)= -a,∴f'(1)=1-a=0⇒a=1是fx x  ≤0的必要条件5分 下证充分性：当a=1时fx  ≤0恒成立 当a=1时，fx  1 1-x =lnx-x+1,f'(x)= -1= ， x x 当x∈0,1  时，f'(x)>0；当x∈1,+∞  时，f'(x)<0， 所以函数y=lnx-x+1在0,1  上单调递增，在1,+∞  上单调递减。 所以fx  ≤f1  =0 综上可知：a=17分 1 1-ax 法二：由题意知,x∈(0,+∞),f(x)= -a= ,1分 x x 当a≤0时,f(x)>0,f(x)在(0,+∞)上单调递增,∴当x∈(1,+∞)时,f(x)>f(1)=0,不符合题意;3分 1 1 1 1 当01由f(x)>0,得x∈(0, ),则f(x)在(0, )上单调递增,所以f( )>f(1)=0,不符合题 a a a a 意;4分 {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}当a=1时,由f(x)>0,得x∈(0,1),则f(x)在(0,1)上单调递增,由f(x)<0,得x∈(1,+∞),则f(x)在(1,+∞) 上单调递减,所以对于任意的x∈(0,+∞),f(x)≤f(1)=0,符合题意;5分 1 1 1 1 当a>1时, <1,由f(x)<0,得x∈( ,+∞),则f(x)在( ,+∞)上单调递减,所以f( )>f(1)=0,不符合题 a a a a 意.6分 综上所述,a=1.7分 法三：由题意得lnx≤a(x-1),x>0. 当x=1时，lnx=a(x-1)恒成立，∴a∈R；1分 lnx 当x>1时，a≥ ,2分 x-1 lnx x-1-xlnx 令F(x)= ,F(x)= , x-1 x(x-1)2 令m(x)=x-1-xlnx,∴当x>1时，m(x)=-lnx<0, m(x)在(1,+∞)上单调递减，m(x)1时，m(x)=-lnx>0, m(x)在(0,1)上单调递增，m(x)1,所以a≤1；6分 x-1 x x→1- x→1- 综上所述，a=1. 7分 (2)法一：要证g(x)≥fx  即证gx  -f(x)≥0.8分 记hx  =gx  -f(x)=x-1  ex-a-lnx+1-ax>0  ，所以hx  1 =xex-a- ，9分 x 令φx  1 =xex-a- ，x∈0,+∞ x  ，所以φx  =1+x  1 ex-a+ >0，所以φx x2  即hx  在0,+∞  上单调递增. 10分 又a∈0,1  1 ，∴h 2  1 1-a = e2 -2<0，h1 2  1 =e1-a-1≥0，∴∃x ∈ ,1 0 2  ，使得hx 0  1 =0，即x ex0-a= ， 0 x 0 1 所以ex0-a= ，x -a=-2lnx ，11分 x2 0 0 0 所以当x∈0,x 0  ，hx  <0，hx  单调递减,当x∈x 0 ,+∞  ，hx  >0，hx  单调递增，所以hx  min =hx 0  = x 0 -1  x -1 ex0-a-lnx +1-a= 0 -3lnx -x +1.13分 0 x2 0 0 0 由(1)知lnx≤x-1，故-lnx 0 ≥-x 0 -1  ，15分 所以hx 0  x -1 ≥ 0 x2 -3x 0 -1 0  -x +1= 1-x 0 0  2x 0 -1  2x 0 +1  .16分 x2 0 1 又x ∈ ,1 0 2  ，所以hx 0  ≥0,故原不等式得证。17分 法二：要证g(x)≥fx  即证gx  -f(x)≥0. 8分 记hx  =gx  -f(x)=x-1  ex-a-lnx+1-ax>0  ，所以hx  1 =xex-a- ，9分 x 令φx  1 =xex-a- ，x∈0,+∞ x  ，所以φx  =1+x  1 ex-a+ >0，所以φx x2  即hx  在0,+∞  上单调递增. 10分 {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}又a∈0,1  1 ，∴h 2  1 1-a = e2 -2<0，h1 2  1 =e1-a-1≥0，∴∃x ∈ ,1 0 2  ，使得hx 0  1 =0，即x ex0-a= ， 0 x 0 1 所以ex0-a= ，x -a=-2lnx ，11分 x2 0 0 0 所以当x∈0,x 0  ，hx  <0，hx  单调递减,当x∈x 0 ,+∞  ，hx  >0，hx  单调递增，所以hx  min =hx 0  = x 0 -1  x -1 ex0-a-lnx +1-a= 0 -3lnx -x +1.13分 0 x2 0 0 0 x-1 1 记t(x)= -3lnx-x+1(x∈ ,1 x2 2  1 2 3 -(x+2)(x2+x-1) ),∴t'(x)=- + - -1= 15分 x2 x3 x x3 1 5-1 5-1 ∴x∈( , )时，x2+x-1<0,∴t'(x)>0,，x∈( ,1)时，x2+x-1>0,t'(x)<0, 2 2 2 1 5-1 5-1 ∴t(x)在( , )单调递增，在( ,1)单调递减 2 2 2 1 1 由于t( )=3ln2-1>0,t(1)=0,∴x∈ ,1 2 2  时，t(x)≥0,∴hx  min =hx 0  ≥0 故hx  ≥0，原不等式得证 17分 法三：主元法 要证g(x)≥fx  即证gx  -f(x)≥0. 8分 记hx  =gx  -f(x)=x-1  ex-a-lnx+1-ax>0  , 以a为主元，记u(a)=x-1  ex⋅e-a-a-lnx+100,∴Q'(x)在(0,+∞)上递增，又Q'(1)=0 x x2 ∴x∈(0,1)时Q'(x)<0,x∈(1,+∞)时Q'(x)>0,∴Q(x)在(0,1)上递减，在(1,+∞)上递增 ∴Q(x)≥Q(1)=0,原不等式得证.17分 19.（17分）已知曲线Γ:x2=4y. t (1)若点T(t,s)是Γ上的任意一点,直线l:y= x-s,判断直线l与Γ的位置关系并证明. 2 (2)若E是直线y=-1上的动点,直线EA与Γ相切于点A,直线EB与Γ相切于点B. ①试问∠AEB是否为定值?若是,求出该定值;若不是,请说明理由. |EB| |AB| ②若直线EA,EB与x轴分别交于点C,D证明: = |EC| |CD| t (1)将y= x-s代人x2=4y,得x2-2tx+4s=0.2分 2 ∴Δ=4t2-16s=0,3分 ∴直线l与Γ相切4分 x2 x2 x x2 x x2 (2)法一①：设A(x, 1),B(x , 2),由（1）知切线AE为y= 1x- 1,BE为y= 2x- 2,5分 1 4 2 4 2 4 2 4 xx 联立得y = 1 2,7分 E 4 xx 又E在直线y=-1上，故 1 2 =-1,8分 4 x x xx ∴k ⋅k = 1 ⋅ 1 = 1 2 =-1, 9分 AE BE 2 2 4 故EA⊥EB,故∠AEB=90°10分 ②设Ax 1 ,y 1  ,Bx 2 ,y 2  x2 x2 2 - 1 y -y 4 4 x +x , 直线AB的斜率为K, 倾斜角为θ,则K=tanθ= 2 1 = = 1 2 11分 x -x x -x 4 2 1 2 1 {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}不妨设直线EA的斜率k >0, 倾斜角为θ,直线EB的斜率k <0, 倾斜角为θ , 1 1 2 2 x x 所以tan∠ECD=tanθ = 1,tanθ = 2 13分 1 2 2 2 tan∠EBA=tanθ-θ 2  -4 x - x +x x x -x 1 x 1 2 - 2 1 2 1 tanθ-tanθ 4 2 4 4 x = 2 = = = = 1, 1+tanθ⋅tanθ 2 1+ x 1 + 4 x 2 ⋅ x 2 2 1+ x 1 x 2 8 +x2 2 1+ -4+( - x 4 1 )2 2 8 则tan∠EBA=tan∠ECD, 所以∠EBA=∠ECD,15分 又EA⊥EB, 所以 RtΔEBA∾RtΔECD, |EB| |AB| 所以 = , 得证.17分 |EC| |CD| 法二①设E(m,-1),设过点E的直线为y+1=k(x-m),与x2=4y联立,得x2-4kx+4km+4=0, 6分 则Δ=16k2-16(km+1)=0即k2-km-1=0, 7分 设直线EA,EB的斜率分别为k,k ,∴k,k 是方程k2-km-1=0的两根 1 2 1 2 则kk =-1,k +k =m,9分 1 2 1 2 故EA⊥EB,故∠AEB=90°.10分 ②设Ax 1 ,y 1  ,Bx 2 ,y 2  x2 x2 2 - 1 y -y 4 4 x +x , 直线AB的斜率为K, 倾斜角为θ,则K=tanθ= 2 1 = = 1 2, 11分 x -x x -x 4 2 1 2 1 由x2-4kx+4km+4=0有唯一解, 可得解为x=2k,可得x =2k, 同理可得x =2k , 1 1 2 2 x +x 2k +2k m 所以K= 1 2 = 1 2 = ,12分 4 4 2 不妨设直线EA的斜率k >0, 倾斜角为θ,直线EB的斜率k <0, 倾斜角为θ , 1 1 2 2 所以tan∠ECD=tanθ =k,13分 1 1 tan∠EBA=tanθ-θ 2  m -k tanθ-tanθ 2 2 m-2k = 2 = = 2, 1+tanθtanθ mk 2+mk 2 1+ 2 2 2 所以tan∠EBA-tan∠ECD= m-2k 2 -k = m-2k 2 -k 12+mk 2 2+mk 1 2  2m-2m = =0, 2+mk 2+mk 2 2 则tan∠EBA=tan∠ECD, 所以∠EBA=∠ECD,15分 又EA⊥EB, 所以 RtΔEBA∾RtΔECD, |EB| |AB| 所以 = , 得证.17分 |EC| |CD| {#{QQABDYCEggAAAAAAAAhCAw0oCkOQkAEAACoGgFAIMAABCQFABAA=}#}