文档内容
合肥一中 2024 届高三最后一卷
数学参考答案
1.已知向量a =(2,3),b=(−1,3),则 a−2b =( )
A.2 B.3 C.4 D.5
【答案解析】a−2b=(2,3)−(−2,6)=(4,−3), a−2b =5,选D
2.已知复数z满足z⋅(1+i)=2−i,则z =( )
1 3 1 3 1 3 1 3
A. + i B. − i C.− − i D.− + i
2 2 2 2 2 2 2 2
2−i 1 3 1 3
【答案解析】z = = − i,z = + i,∴选A
1+i 2 2 2 2
2
3.已知焦点在x轴上的椭圆的离心率为 ,焦距为2 2,则该椭圆的方程为( )
3
x2 x2 x2 y2 x2 y2
A. + y2 =1 B. + y2 =1 C. + =1 D. + =1
3 9 9 7 36 28
c 2 2 x2 y2
【答案解析】 = = ,a =3,a2 =9,b2 =9−2=7, + =1,选C
a 3 a 9 7
4.已知等比数列{a }的前n项和为S ,且S =14,a =2,则a =( )
n n 3 3 4
2 2 2
A.1 B. 或-1 C.− D.− 或1
3 3 3
1 1 2
【答案解析】由S =14,a =2,∴q = 或q =− ,∴a = − 或1,∴选D
3 3 2 3 4 3
1− 5 α
5.已知α为三角形的内角,且cosα= , 则sin =( )
4 2
−1+ 5 1+ 5 3− 5 3− 5
A. B. C. D.
4 4 8 4
α 1−cosα 3+ 5 1+ 5
【答案解析】sin = = = ,选B
2 2 8 4
合肥一中2024届高三最后一卷·数学参考答案 第1页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}6.甲乙丙丁戊5名同学坐成一排参加高考调研,若甲不在两端且甲乙不相邻的不同排列方
式的个数为( )
A.36种 B.48种 C.54种 D.64种
【答案解析】先考虑甲乙不相邻的不同排列方式数,再减去甲站在一端且甲乙不相邻的
排列方式数,所以总数为A3A2 −A1A1A3 =36种,选A
3 4 2 3 3
7.已知四棱锥P−ABCD的各顶点在同一球面上,若AD=2AB=2BC =2CD=4,
∆PAB为正三角形,且面PAB ⊥面ABCD,则该球的表面积为( )
13 52
A. π B.16π C. π D.20π
3 3
3
【答案解析】如图,OE = FG = ,AE =2,
3
3 13
∴R2 =OE2 + AE2 =( )2 +22 = ,
3 3
52
∴S =4πR2 = π,故选C.
3
π
8.过M(0, p)且倾斜角为α(α∈( ,π))的直线l与曲线C:x2 =2py交于A,B两点,分
2
别过A,B作曲线C的两条切线l ,l ,若l ,l 交于N ,若直线MN 的倾斜角为β.则
1 2 1 2
tan(α−β)的最小值为( )
2
A. B. 2 C.2 2 D.4 2
2
【答案解析】如图设N(x ,y ),则l 为x x= p(y+ y )且过M(0, p),
0 0 AB 0 0
x
∴y =−p且k =tanα= 0 ,
0 p
2p
又设k' =tanβ=− ,∴kk' =−2,
x
0
tanα−tanβ
∴tan(α−β)=
1+tanαtanβ
k−k' 2
= =(−k)+(− )≥2 2 ,
1+kk' k
当且仅当k =− 2时“=”成立,故选C
合肥一中2024届高三最后一卷·数学参考答案 第2页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}9. 下表是某人上班的年收入(单位:万元)与上班年份的一组数据:
年份x 1 2 3 4 5 6 7
收入y
2.9 3.3 3.6 4.4 4.8 5.2 5.9
则下列命题正确的有( )
A.年收入的均值为4.3
B.年收入的方差为1.2
C.年收入的上四分位数为5
D.若y与x可用回归直线方程 y =0.5x+a 来模拟,则a =2.3
30.1
【答案解析】y = =4.3,A正确;
7
1.96+1+0.49+0.01+0.25+0.81+2.56 7.08
s2 = = ≠1.2,B错误;
7 7
7×0.75=5.25,所以上四分位数为5.2,C错误;
a = y−0.5x=4.3−0.5×4=2.3,D正确;
故选AD
10.已知函数 f(x)= 3sinωxcosωx−sin2ωx(ω>0),则下列命题正确的有( )
5
A.当ω=2时,x= π 是y = f(x)的一条对称轴
24
1
B.若| f(x )− f(x )|=2,且|x −x | =π,则ω=
1 2 1 2 min
2
π
C.存在ω∈(0,1),使得的图像向左平移 个单位得到的函数为偶函数
6
7
D.若 f(x)在[0,π]上恰有5个零点,则ω的范围为[2, )
3
π 1
【答案解析】 f(x)=sin(2ωx+ )−
6 2
π 1 5 1
对于A,当ω=2时, f(x)=sin(4x+ )− , f( π)=− ,
6 2 24 2
5
∴x= π 不是y = f(x)的一条对称轴,
24
1
对于B,由题意知,T =2π,∴ω=
2
合肥一中2024届高三最后一卷·数学参考答案 第3页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}π π 1 ωπ π 1
对于C,g(x)=sin(2ω(x+ )+ )− =sin(2ωx+ + )− ,
6 6 2 3 6 2
ωπ π π
若g(x)为偶函数,则 + = +kπ,∴ω=1+3k,矛盾
3 6 2
π π π π 25π 29π
对于D,令t = 2ωx+ ∈[ ,2ωπ+ ],由题意知,2ωπ+ ∈[ , )
6 6 6 6 6 6
7
∴ω∈[2, )
3
故选BD
11.已知函数 f(x)=ex,g(x)=−lnx,则下列命题正确的有( )
1
A.若g(x)≥ax恒成立,则a≤−
e
B.若y = f(x)与y=ax−1相切,则a=2e
C.存在实数a使得y = f(x)−ax和y = g(x)+ax有相同的最小值
D.存在实数a使得方程 f(x)−x=a与x+g(x)=a有相同的根且所有的根构成等差
数列
【答案解析】
lnx lnx lnx−1
对于A,由g(x)≥ax得a≤− ,令h(x)=− ,则h'(x)=
x x x2
合肥一中高三最后一卷 1
∴ y =h(x)在(0,e)单调递减,(e,+∞)单调递增,∴a≤h (x)=h(e)=−
min e
对 于 B , 设 切 点 为 P(x ,ex 0) , 则 切 线 方 程 为 y−ex 0 =ex 0(x−x ) , 即
0 0
y =ex 0x+ex 0(1−x ),
0
ex 0 =a
又y=ax−1,∴ ,∴a(1−lna)=−1(∗)
ex 0(1−x )=−1
0
a=2e不满足(∗)式,∴B错,
对于C,易知当a=1时 y = f(x)−ax和y = g(x)+ax有相同的最小值1,
合肥一中2024届高三最后一卷·数学参考答案 第4页(共12页)
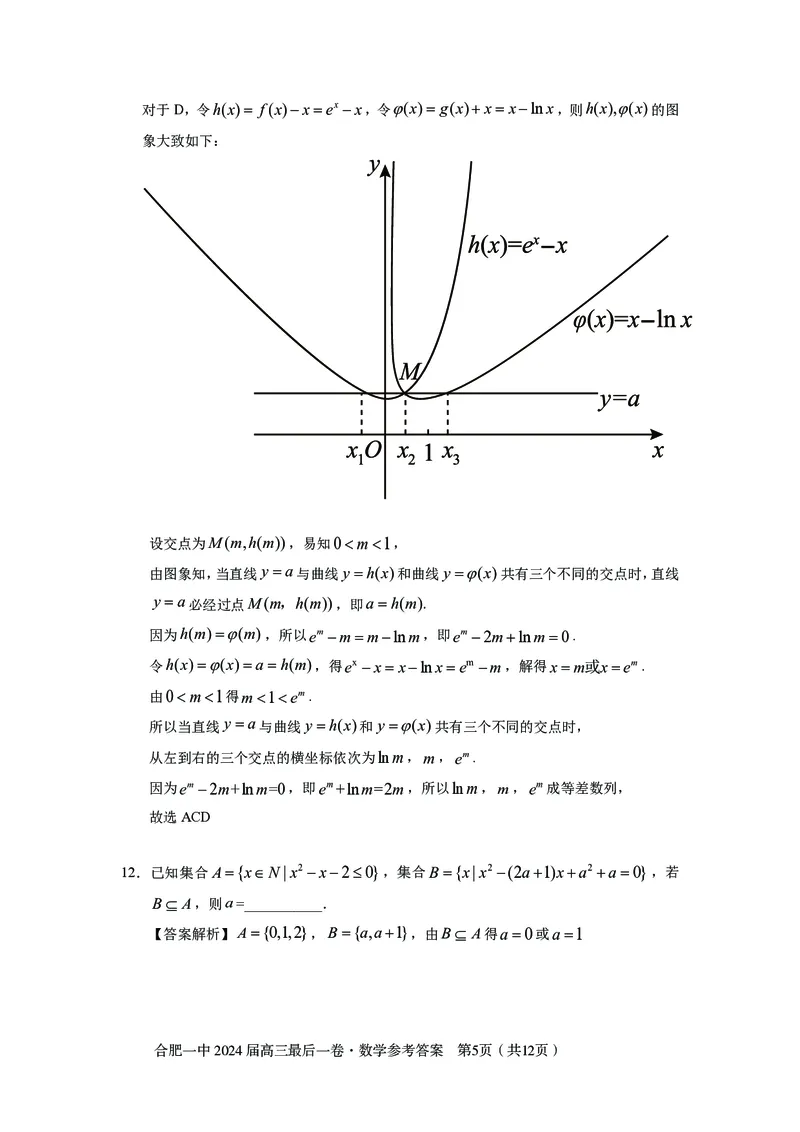
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}对于D,令h(x)= f(x)−x=ex −x,令ϕ(x)= g(x)+x= x−lnx,则h(x),ϕ(x)的图
象大致如下:
设交点为M(m,h(m)),易知02bccosA=b2 +c2 −a2,
b2 +c2 b2 +c2
a2 > ,a> .
2 2
15. 正方体ABCD− ABC D 的棱长为2,P是线段AB上的动点.
1 1 1 1 1
(1)求证:平面BDDB ⊥平面ABC ;
1 1 1 1
6
(2)PB 与平面ABC 所成的角的正弦值为 ,求PB的长.
1 1 1
3
【答案解析】
(1)证明:由题,DD ⊥面ABC D ,四边形ABC D 为正方形,
1 1 1 1 1 1 1 1 1
所以AC ⊥ BD ,AC ⊥ DD ,而BD ∩DD = D,BD ⊂面BDDB ,DD ⊂面
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
合肥一中2024届高三最后一卷·数学参考答案 第6页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}BDDB ,所以AC ⊥面BDDB ,而AC ⊂面 ABC ,所以平面BDDB ⊥平面
1 1 1 1 1 1 1 1 1 1 1 1
ABC .…………………………………………………………………………6分
1 1
(2)设B 在面ABC 上的射影点为E,连接EP,EB ,
1 1 1 1
3
S = ×2 2×2 2 =2 3,
∆A 1 BC 1 4
1 1 1 2 3
V =V ,即 ×2 3×EB = × ×2×2×2,得EB = ,
B 1 −A 1 BC 1 B−A 1 B 1 C 1 3 1 3 2 1 3
设PB 与平面ABC 所成的角的大小为θ,则
1 1 1
2 3
6 EB 3 ,
sinθ= = 1 =
3 PB PB
1 1
所以PB = 2,在∆BPB 中,由余弦定理得,
1 1
π
PB2 = BB2 +PB2 −2BB ×PB×cos ,
1 1 1 4
即2=4+PB2 −2 2PB,解得PB = 2.…………………………………………13分
16.甲和乙进行中国象棋比赛,每局甲赢或输的概率分别为 0.8,0.2,且每局比赛相互独
立.
(1)若比赛采取三局两胜制,且乙已经赢得比赛,则比赛需要的局数X 的数学期望
E(X)为多少?(保留小数点后一位)
(2)由于甲、乙实力悬殊,乙提出“甲赢5局之前乙赢2局则乙胜”,求乙胜的概率.
【答案解析】
(1)P(A)=0.2×0.2+0.2×0.8×0.2+0.8×0.2×0.2=0.104,
0.2×0.2 ( 0.2×0.2×0.8 )×2
所以E(X)=2× +3× ≈2.615≈2.6.………………7分
0.104 0.104
合肥一中2024届高三最后一卷·数学参考答案 第7页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}(2)设 p =0.2,则
0
P(A)= p 2 +[C1p (1− p )]p +[C1p (1− p )2]p +[C1p (1− p )3]p +[C1p (1− p )4]p
0 2 0 0 0 3 0 0 0 4 0 0 0 5 0 0 0
= p 2[1+2(1− p )+3(1− p )2 +4(1− p )3+5(1− p )4]
0 0 0 0 0
=0.04×8.616=0.34464.
……………………………………………………………………………………………15分
17. f(x)=ex−a(a∈R).
(1)若 f(x)的图象在点A(x , f(x ))处的切线经过原点,求x ;
0 0 0
(2)对任意的x∈[ 0,+∞),有 f(x)≥sinx,求a的取值范围.
【答案解析】
ex 0 −a −0
(1) f′(x)=ex−a,所以 f′(x )=ex 0 −a = ,所以x =1;………………5分
0 x −0 0
0
(2)即ex−a −sinx≥0 (∀x≥0 ),令g(x)=ex−a −sinx,
若a≤0,则x−a≥0,ex−a ≥1,g(x)=ex−a −sinx≥1−sinx≥0,合题;…………7分
若a >0,g′(x)=ex−a −cosx,
令h(x)= g′(x),则h′(x)=ex−a +sinx,
当0≤ x≤π时,h′(x)>0,g′(x)递增,而g′(0)=e−a −1<0,g′( π )=e π 2 −a >0,
2
π
所以,存在唯一的x ∈(0, )⊆[0,π],使得g′(x )=ex 0 −a −cosx =0,
0 2 0 0
所以,当0< x< x 时,g′(x)<0,g(x)递减,当x < x<π时,g′(x)>0,g(x)递增,
0 0
π
故g(x) = g(x )=ex 0 −a −sinx =cosx −sinx ≥0,所以0< x ≤ ,
极小 0 0 0 0 0 4
π 2 π ln2
此时,x −a=lncosx ,故a= x −lncosx ≤ −ln ,即0π时,g(x)=ex−a −sinx≥ex−a −1≥e 4 2 −1≥e1−1>0,
合肥一中2024届高三最后一卷·数学参考答案 第8页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}π ln2
因而00,b>0)的上焦点为(0, 6),下顶点为A,渐近线方程
a2 b2
2
是y =± 2x,直线y = 与 y轴交于B点,过B点的直线交双曲线上支于P,Q两点,
3
2
AP,AQ分别交直线y = 于M,N 两点,O坐标原点.
3
(1)求C的方程;
(2)求证:M,N,O,A四点共圆;
(3)求(2)中的圆的半径r的取值范围.
【答案解析】
a
(1)由题,c= 6, = 2,a2 +b2 =c2,解得a2 =4,b2 =2,
b
y2 x2
所以C的方程为 − =1.…………………………………………………………4分
4 2
2 y2 x2
(2)(方法一)设P(x ,y ),Q(x ,y ),PQ: y =kx+ ,代入 − =1,化简整理得
1 1 2 2 3 4 2
k2 −2≠0
4 32 16 32 16
(k2 −2)x2 + kx− =0,有∆= k2 −4(k2 −2) − >0,解得 0
1 2
y +2 2 8x 8x
AP: y = 1 x−2,令y = 得x = 1 ,同理x = 2 ,
x 3 M 3y +6 N 3y +6
1 1 2
8x 8x 64 x x
|BM ||BN |= 1 × 2 = 1 2
3y +6 3y +6 9 (y +2)(y +2)
1 2 1 2
,
64 x x 64 x x 16
= 1 2 = 1 2 =
9 (y +2)(y +2) 9 8 64 9
1 2 k2x x + k(x +x )+
1 2 3 1 2 9
2 2 16
|BO||BA|= ×( +2)= ,|BO||BA|=|BM ||BN |,所以M,N,O,A四点共圆.
3 3 9
……………………………………………………………………………………12分
合肥一中2024届高三最后一卷·数学参考答案 第9页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}(2)(方法二)设OM,AN 的倾斜角分别为α,β.
由对称性,
不妨设PQ的斜率k >0,此时α,β均为锐角,所以
M,N,O,A四点共圆⇔∠AOM +∠ANM =π
π
⇔( +α)+β=π
2
π π
⇔α+β= ,α,β∈(0, )
2 2
⇔ tanαtanβ=1
⇔ k k =1
OM AN
2 y2 x2
设P(x ,y ),Q(x ,y ),PQ: y =kx+ ,代入 − =1,化简整理得
1 1 2 2 3 4 2
k2 −2≠0
4 32 16 32 16
(k2 −2)x2 + kx− =0,有∆= k2 −4(k2 −2) − >0,解得 0
1 2
32 4k
x x = − ,x + x = − ,
1 2 9(k2 −2) 1 2 3(k2 −2)
y +2 2 8x 8x
AP: y = 1 x−2,令y = 得x = 1 ,同理x = 2 ,
x 3 M 3y +6 N 3y +6
1 1 2
y +2 y +2
k = 1 ,k =k = 2 ,
OM 4x AN AQ x
1 2
8 8 8 64
(kx + )(kx + ) k2x x + k(x + x )+
y +2 y +2 1 3 2 3 1 2 3 1 2 9
k k = 1 2 = = =1,
OM AN 4x x 4x x 4x x
1 2 1 2 1 2
所以M,N,O,A四点共圆.……………………………………………………………12分
合肥一中2024届高三最后一卷·数学参考答案 第10页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}(3)设圆心为T ,则
y =−1,
T
x +x 4x 4x 4 x x
x = M N = 1 + 2 = 1 + 2
T 2 3y +6 3y +6 3 8 8
1 2 kx + kx +
1 3 2 3
8
2kx x + (x +x )
4 1 2 3 1 2
= =k
3 8 64
k2x x + k(x +x )+
1 2 3 1 2 9
∴T(k,−1),
5 …………………………………………………………17分
r = k2 +1∈( , 3).
3
n
19.给定自然数 n 且 n≥2 ,设 x ,x ,,x 均为正数, ∑ x =T (T 为常数),
1 2 n i
i=1
n−1 x x
∑ i = n .如果函数 f(x)满足:在区间I 上恒有 f′′(x)>0,则称函数 f(x)
T −x T −x
i=1 i n
1 n 1 n
为凸函数.凸函数 f(x)具有性质: ∑ f(x )≥ f( ∑ x ),.
n i n i
i=1 i=1
x
(1)判断 f(x)= ,x∈(0,1)是否为凸函数,并证明;
1−x
(2)设y =
x
i (i =1,2,,n
合
),证
肥
明:
一 1 中− 高 1 三≤1 最− 后 1 一
;
卷
i T y 1− y n−1
n n
x
(3)求 n 的最小值.
T −x
n
【答案解析】
1 2
(1)f′(x)= , f′′(x)= >0,x∈(0,1),所以 f(x)在(0,1)上为凸函数.
( 1−x )2 (1−x)3
…………………………………………………………………………………………4分
合肥一中2024届高三最后一卷·数学参考答案 第11页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}x n n x 1 n n
(2)y = i (i =1,2,,n)为正数, ∑ y =∑ i = ∑ x =1,即 ∑ y =1,
i T i T T i i
i=1 i=1 i=1 i=1
x x
i n
n−1 x x n−1 n−1 y y
由 ∑ i = n ,得 ∑ T = T , 即 ∑ i = n ,
T −x T −x x x 1− y 1− y
i=1 i n i=11− i 1− n i=1 i n
T T
所以
1 n−1
∑y
y n−1 y n−1 1 n−1 n−1 i 1−y
n =∑ i =∑ f(y )≥(n−1)f( ∑y )=(n−1) i=1 = n ,
1−y 1−y i n−1 i 1 n−1 1−y
n i=1 i i=1 i=1 1− ∑y 1− n
n−1 i n−1
i=1
1− y
1− n
0< y <1(i =1,2,,n),所以1− y n−1 1 1 ,
i n ≤ = −
y 1− y 1− y n−1
n n n
1 1 1 1 1 1
即 −1≤ − ,所以 − ≤1− .……………………………10分
y 1− y n−1 y 1− y n−1
n n n n
x
n
x y 1
T
(3) n = = n = −1关于y 在(0,1)递增,
T −x x 1− y 1− y n
n 1− n n n
T
3n−4− 5n2 −12n+8 1
由(2)解得(y ) = (n≥3);当n=2时,y ≥ .
n min 2(n−2) n 2
x 5n2 −12n+8+2−n
所以 n = (n≥3);当n=2时也成立.
T −x 2(n−1)
n min
1− y 5n2 −12n+8−n
当n≥3时,当且仅当y = y == y = n = 时取“=”;当
1 2 n−1 n−1 2(n−2)(n−1)
1
n=2时,当且仅当y = y = 时取“=”.
1 2 2
x 5n2 −12n+8+2−n
所以 n 的最小值是 .………………………………17分
T −x 2(n−1)
n
合肥一中2024届高三最后一卷·数学参考答案 第12页(共12页)
{#{QQABJYSUggCAAIAAARhCUwXgCAOQkACCCCoOBEAMMAIACBFABAA=}#}