文档内容
南通市 2024 届高三第二次调研测试
数学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上指定位
置上,在其他位置作答一律无效。
3.本卷满分为150分,考试时间为120分钟。考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是
符合题目要求的。
1.已知单位向量 , 的夹角为120°,则
A.-2 B.0 C.1 D.2
2.在正方体 中,下列关系正确的是
A. B. C. D.
3.一组样本数据删除一个数后,得到一组新数据:10,21,25,35,36,40.若这两组数据的中位数相等,
则删除的数为
A.25 B.30 C.35 D.40
4.已知函数 则
A. B. C. D.
5.设 , , ,则 的最小值为
学科网(北京)股份有限公司
学科网(北京)股份有限公司A. B. C. D.3
6.若函数 有大于零的极值点,则实数a的取值范围为
A. B. C. D.
7.设抛物线 的焦点为F,C的准线与x轴交于点A,过A的直线与C在第一象限的交点为M,
N,且 ,则直线MN的斜率为
A. B. C. D.
8.若cosα, , 成等比数列,则sin2α=
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目
要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知双曲线 的右焦点为F,直线 是C的一条渐近线,P是l上一点,
则
A.C的虚轴长为 B.C的离心率为
C.|PF|的最小值为2 D.直线PF的斜率不等于
10.已知 , .若随机事件A,B相互独立,则
学科网(北京)股份有限公司
学科网(北京)股份有限公司A. B. C. D.
11.已知函数f(x),g(x)的定义域均为R,f(x)的图象关于点(2,0)对称, ,
,则
A.f(x)为偶函数 B.g(x)为偶函数 C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.设 ,i为虚数单位.若集合 , ,且 ,则m=
________.
13.在△ABC中, , ,M为BC的中点, ,则AM=________.
14.若正四棱锥的棱长均为2,则以所有棱的中点为顶点的十面体的体积为________,该十面体的外接球的
表面积为________.
四、解答题:本题共5小题,共77分。解答时应写出文字说明、证明过程或演算步骤。
15.(13分)甲公司推出一种新产品,为了解某地区消费者对新产品的满意度,从中随机调查了1000名消
费者,得到下表:
满意 不满意
男 440 60
女 460 40
(1)能否有95%的把握认为消费者对新产品的满意度与性别有关;
(2)若用频率估计概率,从该地区消费者中随机选取3人,用X表示不满意的人数,求X的分布列与数学期
望.
附: , .
0.1 0.05 0.01
k 2.706 3.841 6.635
16.(15分)设函数 .已知f(x)的图象的两条相邻对称轴间的距离
学科网(北京)股份有限公司
学科网(北京)股份有限公司为 ,且 .
(1)若f(x)在区间(0,m)上有最大值无最小值,求实数m的取值范围;
(2)设l为曲线 在 处的切线,证明:l与曲线 有唯一的公共点.
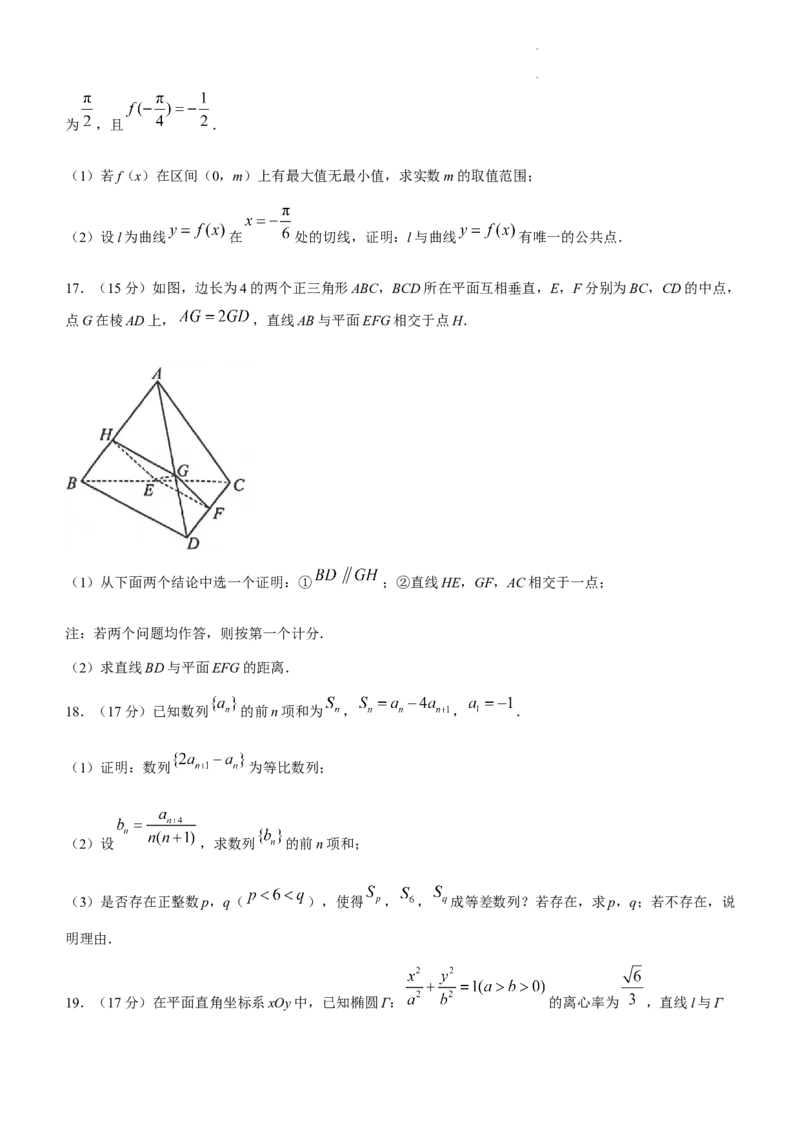
17.(15分)如图,边长为4的两个正三角形ABC,BCD所在平面互相垂直,E,F分别为BC,CD的中点,
点G在棱AD上, ,直线AB与平面EFG相交于点H.
(1)从下面两个结论中选一个证明:① ;②直线HE,GF,AC相交于一点;
注:若两个问题均作答,则按第一个计分.
(2)求直线BD与平面EFG的距离.
18.(17分)已知数列 的前n项和为 , , .
(1)证明:数列 为等比数列;
(2)设 ,求数列 的前n项和;
(3)是否存在正整数p,q( ),使得 , , 成等差数列?若存在,求p,q;若不存在,说
明理由.
19.(17分)在平面直角坐标系xOy中,已知椭圆Γ: 的离心率为 ,直线l与Γ
学科网(北京)股份有限公司
学科网(北京)股份有限公司相切,与圆O: 相交于A,B两点.当l垂直于x轴时, .
(1)求Γ的方程;
(2)对于给定的点集M,N,若M中的每个点在N中都存在距离最小的点,且所有最小距离的最大值存在,
则记此最大值为d(M,N).
(ⅰ)若M,N分别为线段AB与圆O,P为圆O上一点,当△PAB的面积最大时,求d(M,N);
(ⅱ)若d(M,N),d(N,M)均存在,记两者中的较大者为H(M,N).已知H(X,Y),H(Y,
Z),H(X,Z)均存在,证明: .
学科网(北京)股份有限公司
学科网(北京)股份有限公司