文档内容
邵阳市二中 2024 年高三(5 月)模拟考试数学试卷
满分:150 时间120min 命题:高三备课组
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.已知复数 ,则 ( )
A. B. C. D.
2.若数列 满足 , ,则其前2023项和为( )
A.1360 B.1358 C.1350 D.1348
3.已知底面边长为2的正四棱柱 的体积为 ,则直线 与 所成角的余弦为(
)
A. B. C. D.
4.已知直线 : 与圆 : ,过直线 上的任意一点 作圆 的切线 , ,切
点分别为 , ,则 的最大值为( )
A. B. C. D.
5.邵阳市二中高一、高二、高三年级的优秀团员各两名站成一排拍照,恰有一个年级的团员相邻的站法有
( )
A.144种 B.240种 C.288种 D.336种
6.某学习小组对一组数据 进行回归分析,甲同学首先求出回归直线方程 ,
样本点的中心为 .乙同学对甲的计算过程进行检查,发现甲将数据 误输成 ,将这两个数
据修正后得到回归直线方程 ,则实数 ( )
A. B. C. D.
7.若过点 可以作曲线 的两条切线,则( )
A. B. C. D.
学科网(北京)股份有限公司8.已知 , 分别是双曲线 : 的左、右焦点, 为坐标原点,过 的直线分
别交双曲线左、右两支于 , 两点,点 在 轴上, , 平分 , 与其中一
条渐近线交于点 ,则 ( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题
目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知 , , ,则( )
A. B. C. D.
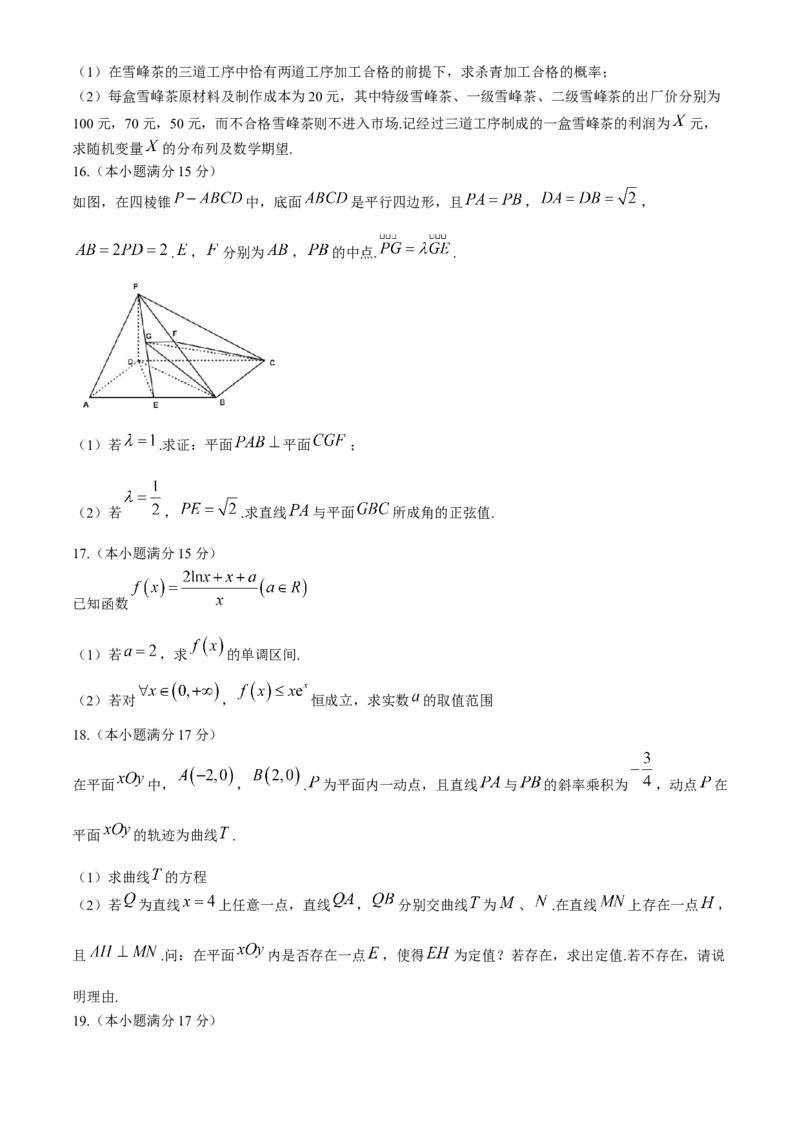
10.如图,已知抛物线 : 的焦点为 ,抛物线 的准线与 轴交于点 ,过点 的直
线 (直线 的倾斜角为锐角)与抛物线 相交于 , 两点( 在 轴的上方, 在 轴的下方),过
点 作抛物线 的准线的垂线,垂足为 ,直线 与抛物线 的准线相交于点 ,则( )
A.当直线 的斜率为1时,
B.若 ,则直线 的斜率为2
C.存在直线 使得
D.若 ,则直线 的倾斜角为
学科网(北京)股份有限公司11.已知非零函数 及其导函数 的定义域均为 ,函数 和 均为奇函数,
且 ,则( )
A.函数 为偶函数 B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12. , ,则 ________.
13.已知数列 与 均为等差数列 ,且 ,则 ________.
14.十七世纪法国数学家、被誉为业余数学家之王的皮埃尔・德・费马提出的一个著名的几何问题:“已知
一个三角形,求作一点,使其与这个三角形的三个顶点的距离之和最小”,意大利数学家托里拆利给出了
解答,当 的三个内角均小于 时,使得 的点 即为费马点;
当 有一个内角大于或等于 时,最大内角的顶点为费马点.已知 , , 分别是 三个
内角 , , 的对边,且 ,若点 为 的费马点, ,则实数
的取值范围为________.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(本小题满分13分)
古楼雪峰茶,产于洞口县古楼,1991年被评为湖南省名茶.其中雪峰茶在制茶过程中,在采摘后还需要经
过杀青、揉捻、干燥这三道工序.现在某雪峰茶厂将采摘后的茶叶进行加工,其中杀青、揉捻、干燥这三道
工序合格的概率分别为 , ,每道工序的加工都相互独立,且茶叶加工中三道工序至多有两道工序
合格的概率为 .三道工序加工都合格的雪峰茶为特级雪峰茶,恰有两道工序加工合格的雪峰茶为一级雪
峰茶,恰有一道工序加工合格的雪峰茶为二级雪峰茶,其余的为不合格雪峰茶.
学科网(北京)股份有限公司(1)在雪峰茶的三道工序中恰有两道工序加工合格的前提下,求杀青加工合格的概率;
(2)每盒雪峰茶原材料及制作成本为20元,其中特级雪峰茶、一级雪峰茶、二级雪峰茶的出厂价分别为
100元,70元,50元,而不合格雪峰茶则不进入市场.记经过三道工序制成的一盒雪峰茶的利润为 元,
求随机变量 的分布列及数学期望.
16.(本小题满分15分)
如图,在四棱锥 中,底面 是平行四边形,且 , ,
. , 分别为 , 的中点. .
(1)若 .求证:平面 平面 ;
(2)若 , .求直线 与平面 所成角的正弦值.
17.(本小题满分15分)
已知函数
(1)若 ,求 的单调区间.
(2)若对 , 恒成立,求实数 的取值范围
18.(本小题满分17分)
在平面 中, , . 为平面内一动点,且直线 与 的斜率乘积为 ,动点 在
平面 的轨迹为曲线 .
(1)求曲线 的方程
(2)若 为直线 上任意一点,直线 , 分别交曲线 为 、 .在直线 上存在一点 ,
且 .问:在平面 内是否存在一点 ,使得 为定值?若存在,求出定值.若不存在,请说
明理由.
19.(本小题满分17分)
学科网(北京)股份有限公司高中教材必修第二册选学内容中指出:设复数 对应复平面内的点 ,设 , ,
则任何一个复数 都可以表示成: 的形式,这种形式叫做复数三角形式,其
中 是复数 的模, 称为复数 的辐角,若 ,则 称为复数 的辐角主值,记为 。复数
有以下三角形式的运算法则:若 ,则:
,特别地,如果
,那么 ,这个结论叫做棣
莫弗定理。请运用上述知识和结论解答下面的问题:
(1)求复数 , 的模 和辐角主值 (用 表示);
(2)设 , ,若存在 满足 ,那么这样的 有多
少个?
(3)求和:
学科网(北京)股份有限公司