2024年湖北云学部分重点高中联盟高三年级10月联考数学试题答案_2024-2025高三（6-6月题库）_2024年10月试卷_10122025届湖北云学部分重点高中联盟高三年级10月联考

2024年湖北云学名校联盟高三年级10月联考 数学试卷评分细则 题号 1 2 3 4 5 6 7 8 9 10 11 选项 C B B D A A B D BC ABD ACD 10 5 12. 13.  3 14. 2 4 12～14题评分细则： 填空题答案没有问题。 12.按照参考答案给分，写错不得分。 13.加上：经检验得 f(x)是偶函数，a  3。 14.解法不唯一。 1.C. [解析]:A 1，,B  0，. AB(1,). sincos2 sin(cossin)(cossin) sin(cossin) 2.B. [解析]:   sincos sincos sin2cos2 tantan2 2   . tan21 5 3. B. [解析]: 由S 18, 得a 2. 由a ,a ,a 等比, 得a2 a a (a d)2 (a 2d)(a d), 9 5 3 4 6 4 3 6 5 5 5 2 2 所以d  (d 0舍去). a a 2d  . 3 3 5 3 π π π 4.D. [解析]:由 f(x3) f(x)0,可得sin(x3 )sin(x )sin(xπ  )恒成立. 6 6 6 2k1 π 5π 7π 32kππ(kz) π.又0, ,π, , ,3π, 3 3 3 3 5.A. [解析]:设ABCD的对角线ACBD O ,AC，BD夹角为，则 1 1 1 1 S  |AO||BO|sin |AO||OD|sin |OC ||BO|sin |OC ||OD|sin ABCD 2 2 2 2 1  | AC||BD|sin, 2   ACBD 46 2 5 5 又 cos     ,所以sin ， AC  BD 5 5 5 5 湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第1页 (共8页)1 1 5 5 故S  |AC ||BD|sin 5 5  ABCD 2 2 5 2 . π π 1 6.A. [解析]:在[0, ], f '(x)sinxa0恒成立, 即a(sinx) sin  . 6 min 6 2 7.B. [解析]:设| AB|| AF |1，由AF  AF , 则|BF ||BF | 2 | AF || AB||BF |1 2. 2 1 2 1 2 1 1 2a| AF || AF | 2. 1 2 在RTAFF 中有 2c 2 |FF |2| AF |2 | AF |2  1 2 2 12 42 2. 1 2 1 2 1 2 c  2c  2 42 2 所以e      2 2. a 2a 2 1 a ax2 xa 8. D. [解析]: f '(x) a  , 由题意,ax2 xa 0(a  0)有两不等正根,所以 x x2 x2 1 1 a 0,14a2 00a ,且x x  ,x x 1. 2 1 2 a 1 2 a f(x x )ln(x x )a(x x ) lna1a2. 1 2 1 2 1 2 x x 1 2 1 1 2a2 1 1 记g(a)lna1a2(0a ) , 则 g'(a) 2a  <0在 0a 恒成立, 从而 2 a a 2 1 3 f(x x ) g(a)lna1a2在0a 单调递减, 其取值范围为(ln2 ,). 1 2 2 4 1 1 5 9.BC. [解析]:选项A: A与B互斥, 则P(AB)P(A)P(B)   . 选项A不正确. 2 3 6 1 1 1 选项B: A与B相互独立, P(AB) P(A)P(B)   , 2 3 6 1 1 1 2 从而P(AB)P(A)P(B)P(AB)    . 选项B正确. 2 3 6 3 1 1 1 选项C: P(A)P(AB)P(AB)P(AB)P(A)P(AB)   P(A)P(B). 选项C正确. 2 3 6 1 选项D: B发生时A一定发生, 则B A, P(AB)P(B)  P(A)P(B). 选项D不正确. 3 02abc2aaa4aa0, 10.ABD. [解析]: 选项A:  选项A正确. 02abc2ccc4cc0, c a c c c c a 选项B:  [( )( )]2 ( )( ) 2. 而 1,等号不成立. 选项B正确. a c a a a a c 湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第2页 (共8页)选项C: 2ac2ab2acc2abc0, 所以ac0. 选项C不正确. ac 选项D:2abc0ac(ab) 1. 由选项C不正确,ac0,可知ab0 . ab a2c ac c c    1 1.选项D正确. ab ab ab ab π π π 11. ACD. [解析]: 选项A: 易知 , sinsinsin( )sin 2sin( ) . 2 2 4 π π π 3π π 2 又0 ,   , 从而sin( ) , 所以sinsin1. 选项A正确. 2 4 4 4 4 2 tantan 选项B: tan() 0,tantan1. 选项B不正确. 1tantan π π 选项C: coscoscos( )cos 2sin( ) 2. 选项C正确. 2 4  tan π  1  选项D: 易知0 ,tan (0,1). tan() 2  tan . 选项 2 2 2  2 1tan2( ) 2 D正确. 10 z 12. . [解析]: 由 2i, 得z (2i)(zi)(2i)z(2i)i (i1)z(2i)i 2 zi (2i)i |(2i)i| |(2i)||i| 51 10  z  . |z|    . i1 |i1| |i1| 2 2 π π 3 3 13.  3. [解析]: 令 f( ) f( ), 得  a3 a   3. 6 6 2 2 5 14. .[解析]: 由题意可知P的轨迹为以A为圆心，1为半径的且在直角梯形ABCD内部的一 4 段圆弧，以 A为原点建立平面直角坐标系，使得 A  0，0 ，B  1,0  ,D 1,2  ,所以    3π   AB1,0,AD1,2 , 设 Pcos,sin,  ,0 ， 所 以 APcos,sin , 又    4  A B    APABAD,2， P cos 1 1 所以有  ，故 sin，coscos sin，  sin2 2 2 D C 湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第3页 (共8页) 1 1 3 5 4 所以 cos sin sincos sin cos，其中锐角满足cos , 2 2 4 4 4 5 3 sin . 5 3  5 5 而 , 当0时，  cos取得最大值 . 4 2 4 4 15.[解析]：(1) 由S 2S n , n1 n 则当n2时,S 2S (n1),两式相减, 得a 2a 1 ..................................................2分 n n1 n1 n . a 1 2(a 1)(n 2) n1 n . 又当n1时,S a a 2S 12a 1a a 10. 2 1 2 1 1 1 2 当n1时,也有a 1 2 2(a 1)成立...............................................................................3分 2 1 a 1 nN*,总有 n1  2,即{a 1}是以a 11为首项,2为公比的等比数列. ..................4分 a 1 n 1 n a 112n-1. n {a }的通项公式为:a 2n-11(nN*). ...............................................................................6分 n n (2) 由(1)知, b log (a 1)n1. ..............................................................................7分 n 2 n n(n1) T b b b  ................................................................................................9分 n 1 2 n 2 1 2 1 1 当n 2时,   2(  ). ..............................................................................10分 T n(n1) n1 n n 1 1 1 1 1 1 1 1 1 1 1      2[(  ) (  ) (  )] 2(1 ). ....................13分 T T T T 1 2 2 3 n 1 n n 2 3 4 n 说明：第（1）问中没有验证n=1的扣1分。 15题评分细则：按照参考答案标准细则给分，请注意红字部分说明。   16.[解析]:(1) m//n,(2ac)cosB bcosC.....................................................................2分 由正弦定理,得2sin AcosBsinCcosB sinBcosC 2sin AcosB sin A........................4分 1 π 在三角形ABC中, sin A0, 2cosB1cosB ,所以B  ......................................7分 2 3 说明：第（1）问中未标注角的范围扣1分 湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第4页 (共8页)(2)S 2S AD 2DC. ABD DBC 1 1 1 S S S  cBDsinABD aBDsinDBC  acsinB. ...................12分 ABD DBC ABC 2 2 2 π sinABD sinDBC 3 两边同时除以ac, 又B  ,BD(  ) . 3 a c 2 sinABD sinDBC 1 又   , BD 2 3.........................................................................15分 a c 4 16题评分细则：按照参考答案标准细则给分，请注意红字部分说明。 17.[解析]: (1) f '(x)ex a......................................................................................................1分 当a0时, f '(x)ex a 0恒成立, f(x)在R上单调递增..................................................3分 当a 0时, 令f '(x)ex a 0,得x lna;令f '(x)ex a 0,得xlna. f(x)在(,lna)单调递减, 在(lna,)单调递增. ................................................5分 综上所述当a0时, f(x)在R上单调递增; 当a 0时, f(x)(,lna)单调递减, 在(lna,)单调递增. ................................................6分 (2)解法1: ①当a0时, y ex在R上单调递增, 值域为(0,); y ax(1b)在R单调递减,值域为(,). 所以存在实数x , 使得在ex 0 ax (1b). 0 0 且在(,x )上ex 0 ax (1b),即f(x )0,不满足条件. 0 0 0 .........................................................8分 ②当a 0时, 若 f(x)ex b101bex恒成立,即1b0b1.此时ab1. ...10分 此处只要能说明a<0或者a=0时不等式不恒成立即可不扣分 ③当a 0时, 由(1)知, f(x)在(,lna)单调递减, 在(lna,)单调递增. 则 f(x)  f(lna)aalnab10balnaa1. abalna1. min .....................12分 1 记h(a)alna1(a 0),则h'(a)lna1.令h'(a)0, 得a  . e 1 1 且在(0, ),h'(a)0,h(a)单调递减;在( ,),h'(a) 0,h(a)单调递增. e e 1 1 1 h(a) h( )1 . 此时ab的最小值为1 1. min e e e 湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第5页 (共8页)1 1 2 综上①②③,ab的最小值为1 .此时a  ,b1 . e e e 此处未注明最小值条件的扣1分...........................................................15分 解法2:y ex在x x 处与y ax (1b)平行的切线为yex 0 ex 0(xx ), 0 0 结合图象, 它在直线 y ax(1b)的上方, 即a ex 0,1b(1x )ex 0. 0 ab1x ex 0.....................................................................................................12分 0 记g(x)1xex,则g'(x)(x1)ex. 在(,1)上,g'(x)0,从而g(x)单调递减;在(1,)上,g'(x)0, 从而g(x)单调递增. 1 g(x)有最小值g(1)1 . e 1 x 1时,ab取得最小值1 . 0 e 1 2 1 1 2 此时,a ,b .直线y ax(1b)恰好为 y ex在点(1, )处的切线y  x .此处未注 e e e e e 明最小值条件的扣1分........15分 17题评分细则：按照参考答案标准细则给分，请注意红字部分说明。 18.[解析]：(1)由于ACBCAD 90，则AD//BC . 又BC 平面PAD,AD 平面PAD , 所以BC //平面PAD . 又BC 平面PBC,平面PBC平面PAD l ，则BC//l.........................................................3分 PA底面ABCD, PA BC ，又BC  AC ,PAAC C , 所以BC 平面PAC . 又BC //l，所以l 平面PAC ....................................................................................................6分 (2) 取棱CD的中点E. 由题意, 可得CD  AC2AD2  2.           2 1 2  2 7 则MCMD MEEC MEED ME  CD ME 1 , 4 9  2 2 2 可得ME  , ME  为定值.............................................................................................10分 9 3 2 点M 的轨迹是以E为圆心， 为半径且在PCD内的半圆. 3 当点M 在线段PE上时, PM长度的最小. 又PC  PD PA2  AD2  3, PE CD,且PE  PC2 CE2  2. 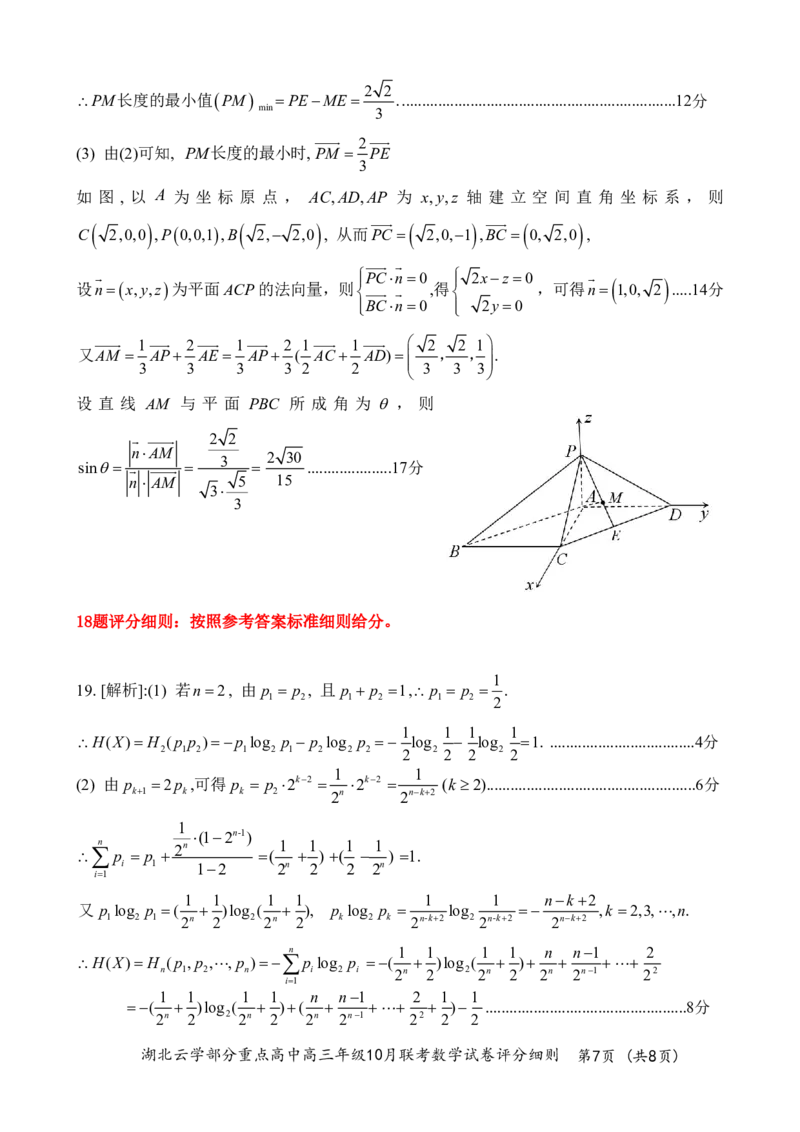湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第6页 (共8页)2 2 PM长度的最小值 PM   PEME  .....................................................................12分 min 3  2 (3) 由(2)可知, PM长度的最小时, PM  PE 3 如 图 , 以 A 为 坐 标 原 点 ， AC,AD,AP 为 x,y,z 轴 建 立 空 间 直 角 坐 标 系 ， 则           C 2,0,0 ,P  0,0,1 ,B 2, 2,0 , 从而PC  2,0,1 ,BC  0, 2,0 ,     PCn0   2xz 0    设n x,y,z 为平面ACP的法向量，则   ,得  ，可得n 1,0, 2 .....14分 BCn0  2y 0  1 2 1 2 1 1  2 2 1 又AM  AP AE  AP ( AC AD) ， ，.   3 3 3 3 2 2  3 3 3 设 直 线 AM 与 平 面 PBC 所 成 角 为  ， 则   2 2 nAM sin    3  2 30 .....................17分 n  AM 5 15 3 3 18题评分细则：按照参考答案标准细则给分。 1 19.[解析]:(1) 若n2, 由 p  p , 且 p  p 1,p  p  . 1 2 1 2 1 2 2 1 1 1 1 H(X) H (p p )p log p  p log p  log  log 1. ....................................4分 2 1 2 1 2 1 2 2 2 2 2 2 2 2 2 1 1 (2) 由 p 2p ,可得 p  p 2k2  2k2  (k 2)....................................................6分 k1 k k 2 2n 2nk2 1 (12n-1)  n p  p  2n ( 1  1 ) ( 1  1 ) 1. i 1 12 2n 2 2 2n i1 1 1 1 1 1 1 nk2 又p log p (  )log (  ), p log p  log  ,k 2,3,,n. 1 2 1 2n 2 2 2n 2 k 2 k 2n-k2 2 2n-k2 2nk2 n 1 1 1 1 n n1 2 H(X) H (p ,p ,,p )p log p (  )log (  )   n 1 2 n i 2 i 2n 2 2 2n 2 2n 2n1 22 i1 1 1 1 1 n n1 2 1 1 (  )log (  )(    ) ..................................................8分 2n 2 2 2n 2 2n 2n1 22 2 2 湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第7页 (共8页)1 2 n1 n 1 1 2 n1 n 记S     , 则 S     . n 2 22 2n1 2n 2 n 22 23 2n 2n1 1 1( )n 1 1 1 1 n 1 n n 2 两式作差, 得 S       2   1 . 2 n 2 22 2n 2n1 2 1 2n1 2n1 1 2 n2 S  2 ............................................................................................................................10分 n 2n 1 1 1 1 n2 1 H(X)(  )log (  )(2 ) 2n 2 2 2n 2 2n 2 1 1 1 1 n2 3 (  )log (  )  ...........................................................................11分 2n 2 2 2n 2 2n 2 (3) 证明:. 设 （ ） ， ， ∗ = = = 1,2,3⋯, ( ∈ ) = 1 , =1 根据X 和Y 相互独立, P(X i,Y  j) pq . i j n m P(XY k)  pq , pq 1..........................................................................................13分 i j i j ijk i1 j1 H(XY)H (pq ,pq ,,pq ,p q ,,p q ,,p q ,p q ) mn 1 1 1 2 1 m 2 1 2 m n 1 n m n m n m (pq )log (pq ) (pq )(log p log q ) i j 2 i j i j 2 i 2 j i1 j1 i1 j1 n m n m m n n m (pq )(log p )(pq )(log q ) q (p log p ) p (q log q ) i j 2 i i j 2 j j i 2 i i j 2 j i1 j1 i1 j1 j1 i1 i1 j1 n m (p log p )(q log q )  H(X)H(Y), 得证............................................17分 i 2 i j 2 j i1 j1 19题评分细则：按照参考答案标准细则给分。 湖北云学部分重点高中高三年级10月联考数学试卷评分细则 第8页 (共8页)