2025届江西省高三四月适应性联考数学试题_2024-2025高三（6-6月题库）_2025年04月试卷_04222025届江西省高三下学期四月适应性联考（三模）（全科）

工作机密 切勿外传 举报有奖 诚信考试 泄密出现 严肃追责 C． D． ②③ ①②③ 1 6.已知抛物线C的方程为 y x2，F为其焦点，点N坐标为 0,4 ，过点F作直线交抛物线于A,B 准考证号________________姓名________________ 4 （在此卷上答题无效！） 两点，D是x轴上一点，且满足 DA  DB  DN ，则直线AB的斜率为 机密★ 考试时间：2025年4月17日 15 11 2025 年江西省四月适应性联考 A. 2 B. 3 C. D. 2 2 暨普通高等学校招生第三次模拟考试 x2 y2 7.已知x0， y 0且x y 1，则  的最小值为 x1 y2 数 学 试 题 1 1 1 A. B. C.1 D. 4 2 3 1 1  1 本试卷共4页。满分150分，考试时间120分钟。本场考试结束后，请监考员将考 8.已知函数 f(x)  ，则关于t的不等式 f(lnt)2f ln  0的解集为 ex 1 2  t 生的试卷和答题卡一并收回。考生不得在考试信号铃声发出前答题。选择题请用 2B铅笔  1 规范填涂，如需修改，用橡皮擦干净再选涂其他答案标号；非选择题请用0.5 毫米黑色墨 A.(0,) B.0,  C.(0,1) D.(1,) 水签字笔在答题卡规定的黑色矩形边框区域内认真作答，答题规范，书写清晰。  2 二､选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部 一､选择题：本题共8小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要 选对的得6分，部分选对的得部分分，有选错的得0分. 求的. 9.已知某品牌汽车某年销量记录如下表所示： 1.已知集合A  x∣x3x0  ,B  x∣x2x20  ，则AB  月份x 1 2 3 4 5 6 A.  0,1  B. 1,0  C.  0,1,2  D. 1,0,1  销量y（万辆） 11.7 12.4 13.8 13.2 14.6 15.3 2.已知 m,n 是两条不同的直线， , 是两个不同的平面，则m∥ 的一个充分条件是 针对上表数据，下列说法正确的有 A.销量的极差为3.6 A.m∥n,n∥ B.m∥,∥ B.销量的60%分位数是13.2 C.mn,n,m D.mn A,n∥ ,m C.销量的平均数与中位数相等  22025 3. x  的展开式中的常数项是 D.若销量关于月份的回归方程为y0.7xb，则b11.05  x 10．设函数 f(x)ex ex 2x,xR，则下列说法正确的是 A.第673项 B.第674项 C.第675项 D.第676项 A． f(x)是奇函数 B． f(x)在R上是单调函数 4.圆锥SO中，S为圆锥顶点，O为底面圆的圆心，底面圆O半径为3，侧面展开图面积为6 3，底 C． f(x)的最小值为1 D．当x0时， f(x)0 面圆周上有两动点A,B，则△SAB的面积最大值为 11．如图，在棱长为1的正方体ABCD A 1 B 1 C 1 D 1 中，点O为线段BD的中 点，且点P满足 BPBCBB ，则下列说法正确的是 A.3 3 B.4 C.6 D.2 5 1 1 A．若1,0，则V  5．气象意义上从春季进入夏季的标志为“连续5天的日平均温度均不低于22C”．现有甲、乙、丙三地 PA 1 BD 8 连续5天的日平均温度的记录数据(记录数据都是正整数，单位：C)： B．若1，则DP//平面ABD 1 1 甲地：5个数据的中位数为24，众数为22； 1 ① C．若1, ，则OP 平面ABD 乙地：5个数据的中位数为27，总体均值为24； 2 1 ② ③ 丙地：5个数据中有1个数据是32，总体均值为26，总体方差为10.8． D．若1,01时，直线OP与平面ABD所成的角为，则sin[ 2 ,1] 其中肯定进入夏季的地区有 1 3 A． B． ①② ①③ 三模联考数学第 1页 共4页 三模联考数学第 2页 共4页 学科网（北京）股份有限公司 {#{QQABaQC4xgIQgASACR4KE0WmCkkQsIKhJaoswUCUqAwLwYFABIA=}#}三､填空题：本题共3小题，每小题5分，共15分. 17.（本小题满分15分） 目前高考数学多选题6分制的模式改变了传统的多选题赋分模式，每题具有多个正确答案，答对所有 3 12．与直线 y  x和直线 y  3x都相切且圆心在第一象限，圆心到原点的距离为 2的圆的方程 正确选项得满分，答对部分选项也可得分，强调了对知识点理解和全面把握的要求．在某次数学测评 3 3 1 中，第11题（6分制多选题）得分的学生有100人，其中 的学生得部分分， 的学生得满分，若给 为_________． 4 4 13．已知函数 f  x log  4x 2x11  x，若 f  2a1  f  a3  ，则实数a的取值范围为 每位得部分分的学生赠送1个书签，得满分的学生赠送2个书签．假设每个学生在第11题得分情况相 2 互独立． _________． (1)从第11题得分的100名学生中随机抽取4人，记这4人得到书签的总数为X 个，求X 的分布列和 数学期望； 14.清代数学家明安图所著《割圆密率捷法》中比西方更早提到了“卡特兰数”（以比利时数 学家欧仁･查理･卡特兰的名字命名）.有如下问题：在nn的格子中，从左下角出发走到右 (2)从第11题得分的100名学生中随机抽取n人  0n100,nN* ，记这n人得到书签的总数为 n1 上角，每一步只能往上或往右走一格，且走的过程中只能在左下角与右上角的连线的右下方 个的概率为P n ，求P 1 P 2 P 3 P n 的值； （不能穿过，但可以到达该连线），则共有多少种不同的走法？此问题的结果即卡特兰数 (3)已知王老师班有20名学生在第11题有得分，若以需要赠送书签总个数概率最大为依据，请问王老 Cn Cn1 .如图，现有34的格子，每一步只能往上或往右走一格，则从左下角A走到右 师应该提前准备多少个书签比较合理？ 2n 2n 上角B共有__________种不同的走法；若要求从左下角A走到右上角B的过程中只能在直 线AC的右下方，但可以到达直线AC，则有__________种不同的走法. 18.（本小题满分17分） 四､解答题（本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.） 已知动直线l与椭圆C: x2  y2 1交于P  x ,y  ，Q  x ,y  两个不同点，且△OPQ的面积 15.（本小题满分15分） 3 2 1 1 2 2 已知等比数列  a  的前n项和为S ，且a 3S 2  nN*  ． 6 n n n1 n S  ，其中O为坐标原点.   △OPQ 2 （1）求数列 a 的通项公式； n （1）证明x2 x2 和 y2  y2 均为定值； （2）在a 与a 之间插入n个数，使这n2个数组成一个公差为d 的等差数列，在数列  d  中是 1 2 1 2 n n1 n n （2）设线段PQ的中点为M ，求|OM ||PQ|的最大值； 否存在3项d ，d ，d （其中m，k，p成等差数列）成等比数列？若存在，求出这样的3项；若 m k p 6 不存在，请说明理由． （3）椭圆C上是否存在点D，E，G，使得S S S  ？若存在，判断△DEG △ODE △ODG △OEG 2 的形状；若不存在，请说明理由. 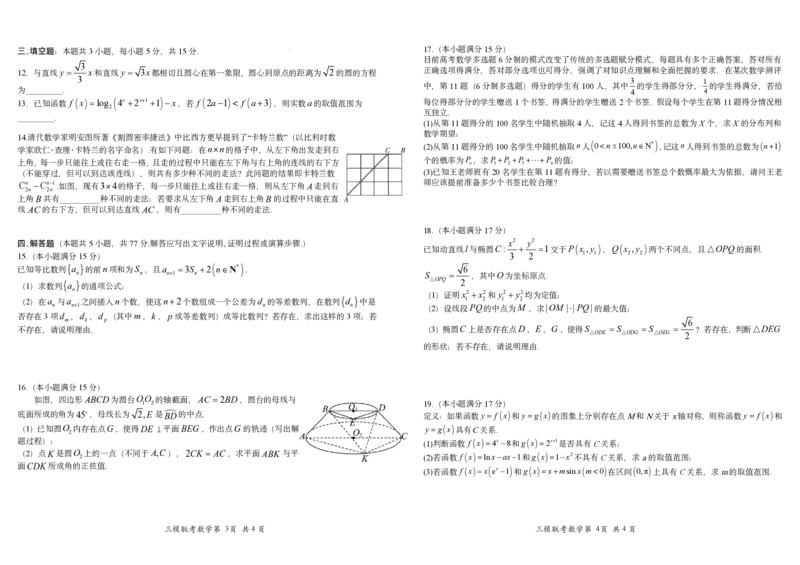16.（本小题满分15分） 如图，四边形ABCD为圆台OO 的轴截面，AC 2BD，圆台的母线与 1 2 19.（本小题满分17分） 底面所成的角为45，母线长为 2,E是B  D的中点. 定义：如果函数y f x 和ygx 的图象上分别存在点M和N关于x轴对称，则称函数y f x 和 （1）已知圆O 2 内存在点G，使得DE 平面BEG ，作出点G的轨迹（写出解 ygx 具有C关系. 题过程）； (1)判断函数 f x4x8和gx2x1 是否具有C关系； （2）点K是圆O 2 上的一点（不同于A,C ），2CK  AC，求平面ABK 与平 (2)若函数 f xlnxax1和gx1x2 不具有C关系，求a的取值范围； 面CDK所成角的正弦值. (3)若函数 f x x  ex 1  和gxxmsinxm0 在区间 0,π 上具有C关系，求m的取值范围. 三模联考数学第 3页 共4页 三模联考数学第 4页 共4页 学科网（北京）股份有限公司 {#{QQABaQC4xgIQgASACR4KE0WmCkkQsIKhJaoswUCUqAwLwYFABIA=}#}