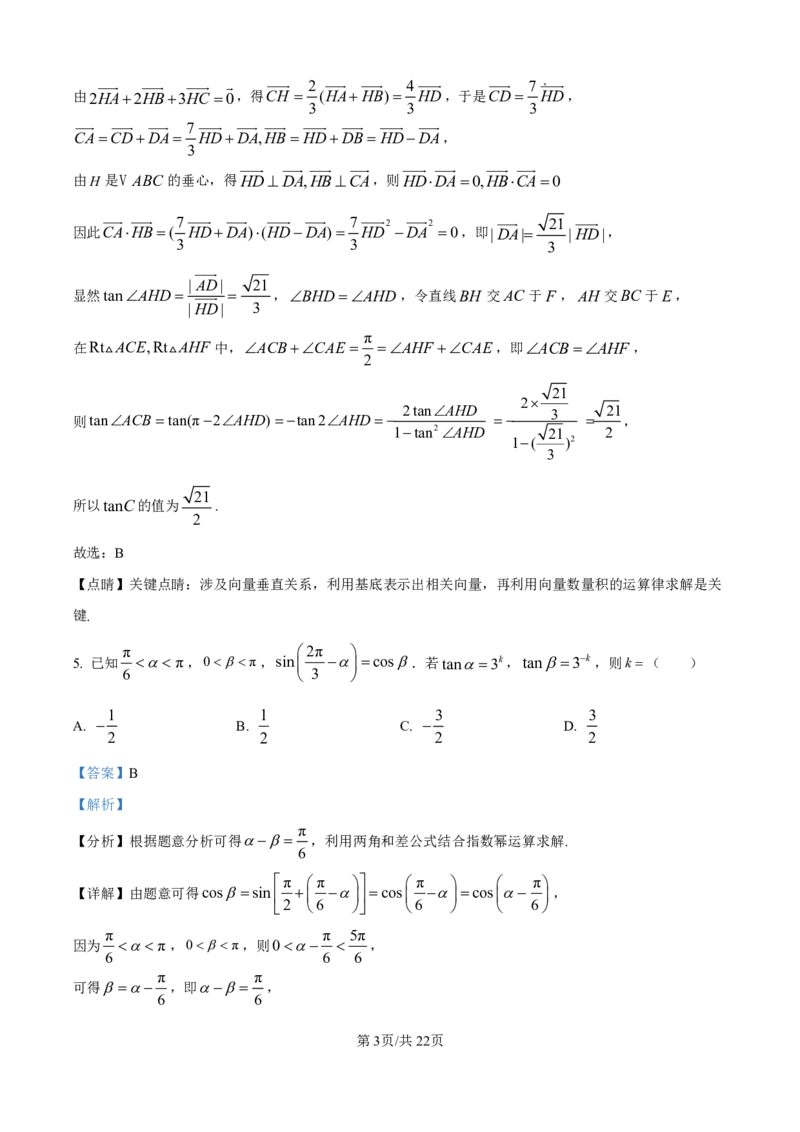2025届河北省衡水中学高三10月综合素质测评（二）-数学试题+答案_2024-2025高三（6-6月题库）_2024年10月试卷_10142025届河北省衡水中学高三10月综合素质测评（二）

高三年级素养检测一数学试题 一、选择题：本题共 8小题，每小题5 分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1. 设集合 M  1,3,a2  ,N   1,a2  ，若 M N  1,4  ，则a （ ） A 2 B.0 C.2 D. 2 . z 2. 已知复数z 12i,z ,z 在复平面内的对应点关于实轴对称，则 1 的虚部为（ ） 1 1 2 z 2 4 4i 4 4i A. B. C.  D.  5 5 5 5 1 2 3. 若log xlog y 2，则  的最小值为（ ） 4 4 x y 2 1 3 1 A. B. C. D. 2 8 4 2     4. 若H 是V ABC 的垂心，2HA2HB3HC 0，则tanC的值为（ ） 21 10 A. 5 B. C. 2 2 D. 2 2 π 2π  5. 已知  π，0π，sin   cos．若tan3k，tan3k，则k （ ） 6  3  1 1 3 3 A.  B. C.  D. 2 2 2 2  1    6. 在V ABC中，BD  BC ，E是线段AD上的动点（与端点不重合），设CE  xCA yCB，则 3 2x3yxy 的最小值是（ ） xy A.10 B.4 C.7 D.13        ab     7. 已知向量 a  b 4,ab 8,c  ，且 nc 1，则n与c夹角的最大值为（ ） 2 π π π 5π A. B. C. D. 6 4 3 12 第1页/共4页 学科网（北京）股份有限公司 1 8. 已知a0， f  x  aex  ln  xb  ，当x 0时， f x0，则a  1b 3的最大值为（ ）  x 1 2 A. B. e2 e2 3 4 C. D. e2 e2 二、多选题：本题共 3小题，每小题6 分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9. 对于函数 f  x  定义域中任意的x ,x  x  x  ，有如下结论，①  x x  f  x  f  x  0， 1 2 1 2 1 2 1 2  x x  f  x  f  x  ② f  x 2  f  2x 0，③ f  1 2   1 2 ，④ f  2x  f  22x 0.下列函数能 1 1 1 1  2  2 同时满足以上两个结论的有（ ） π  A. B. f  x sin x 2  =ln C. f  x ex D. f  x  x3 10. 已知复数z ，z ，z ，则下列说法中正确的有（ ） 1 2 3 1 3 1 3 A. 若z z  z z ，则z 0或z  z B. 若z   i，则z2024   i 1 2 1 3 1 2 3 1 2 2 1 2 2 C 若z2 z2 0，则z  z 0 D. 若z z  z z ，则|z ||z | . 1 2 1 2 1 1 2 2 1 2 11. 已知函数 f  x 2sinxcosx2sin2x1  N*  在   π , π 上有最大值，无最小值，则（ ） 12 3   A. f x 为奇函数 π π   B. f x 在 , 上单调递增 4 2 π C. x 是 f  x  离 y 轴距离最近的对称轴 8 D. f  x  的最小正周期为π 三、填空题：本题共 3小题，每小题 5分，共 15分. 第2页/共4页 学科网（北京）股份有限公司3 12. 已知V ABC 的内角A,B,C 的对边分别为a,b,c，若a 2,b1,△ABC 的面积为 ，则c ______． 2 π 13. 在平面直角坐标系xOy中，一动点从点M ( 3,0)开始，以 rad/s的角速度逆时针绕坐标原点O做匀 0 2 1 3 速圆周运动，xs后到达点M 的位置.设A( , )，记(x)| AM |2，则(x)的单调递增区间为 2 2 _______________ 14. 已知数列  a  满足a a,a  1 a2 2  n1,2,3, ，则 n 1 n1 2 n ①当a1时，存在kN*，使得a 2： k ②当a 1时，  a  为递增数列，且a 2恒成立； n n   ③存在aR，使得 a 中既有最大值，又有最小值； n 1 ④对任意的aR，存在n N*，当nn 时， a 2  恒成立. 0 0 n 2024 其中，所有正确结论的序号为______. 四.解答题：本题共 5小题.解答应写出文字说明、证明过程或演算步骤. 15. 在V ABC 中，角A,B,C .所对的边分别为a,b,c.已知  2ba  cosC ccosA. （1）求C； 3 （2）若V ABC 的内切圆半径为 ,c4，求V ABC 的面积. 2 π π π π 2π 16. 已知函数 f(x)sin(x)在区间( , )单调，其中为正整数，|| ，且 f( ) f( ). 6 2 2 2 3 （1）求y f(x)图象的一条对称轴； π 3 （2）若 f( ) ，求 . 6 2 1  a n,n为奇数, 17. 设S 是数列  a  的前n项和，已知a 1，a 2 n n n 1 n1  a 2n,n为偶数. n （1）证明：  a 2  是等比数列； 2n （2）求满足S 0的所有正整数n. 2n 第3页/共4页 学科网（北京）股份有限公司x e 18. 已知函数 f  x 2cos2  1,x 0,2π  . 2 ex （1）证明： f  x 的导函数有且仅有一个极值点；   （2）证明： f x 的所有零点之和大于2π. 19. 定理：如果函数 f (x)在闭区间[a，b]上的图象是连续不断的曲线，在开区间(a,b)内每一点存在导数， 且 f(a) f(b)，那么在区间(a,b)内至少存在一点c，使得 f(c)0，这是以法国数学家米歇尔罗尔的 名字命名的一个重要定理，称之为罗尔定理，其在数学和物理上有着广泛的应用. （1）设 f(x) x(x1)(x2)(x4)，记 f (x)的导数为 f(x)，试用上述定理，说明方程 f(x)0根的 个数，并指出它们所在的区间； （2）如果 f (x)在闭区间[a，b]上的图象是连续不断的曲线，且在开区间(a,b)内每一点存在导数，记 f (x) 的导数为 f(x)，试用上述定理证明：在开区间(a,b)内至少存在一点c，使得 f(b) f(a) f(c)(ba)； ab （3）利用（2）中的结论，证明：当0ab时， (ab)e 2 aea beb.（e为自然对数的底数） 第4页/共4页 学科网（北京）股份有限公司高三年级素养检测一数学试题 一、选择题：本题共 8小题，每小题5 分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1. 设集合 M  1,3,a2  ,N   1,a2  ，若 M N  1,4  ，则a （ ） A. 2 B.0 C.2 D. 2 【答案】C 【解析】 【分析】根据给定条件，利用交集的结果列出方程求解即得. 【详解】集合M  1,3,a2  ,N   1,a2  ，而M N  1,4  ，则a2a2 4， 经验证 符合题意，所以a2. 故选： C=2 z 2. 已知复数z 12i,z ,z 在复平面内的对应点关于实轴对称，则 1 的虚部为（ ） 1 1 2 z 2 4 4i 4 4i A. B. C.  D.  5 5 5 5 【答案】A 【解析】 【分析】根据对称性求复数z ，再根据复数的除法运算公式，即可化简求解. 2 【详解】由题意得z 在复平面内所对应的点为  1,2  ，则z 所对应的点为  1,2  ，所以z 12i， 1 2 2 z 12i (12i)2 34i 4 则 1    ，虚部为 . z 12i  12i  12i  5 5 2 故选：A. 1 2 3. 若log xlog y 2，则  的最小值为（ ） 4 4 x y 2 1 3 1 A. B. C. D. 2 8 4 2 【答案】A 【解析】 第1页/共22页 学科网（北京）股份有限公司1 2 2 【分析】首先过呢据条件化简得到xy 16，法一，根据基本不等式  2 ，即可求解；法二， x y xy 1 2 y 2 根据条件等式，变形得    ，再利用基本不等式，即可求解. x y 16 y 【详解】log xlog y2,x0,y0,log  xy 2,xy16， 4 4 4 1 2 2 2 2 1 2 法一：  2 2  ，当且仅当  时，上式等号成立， x y xy 16 2 x y 1 2 2 又xy 16，可得x2 2,y 4 2 时，  的最小值为 . x y 2 故选：A. 1 2 y 2 2 y 2 法二：     ，当且仅当  时，上式等号成立， x y 16 y 2 16 y 1 2 2 又xy 16，可得x2 2,y 4 2 时，  的最小值为 . x y 2 故选：A.     4. 若H 是V ABC 的垂心，2HA2HB3HC 0，则tanC的值为（ ） 21 10 A. 5 B. C. 2 2 D. 2 2 【答案】B 【解析】  7 【分析】取AB的中点D，连接HD，利用中点向量公式结合给定等式推得CD  HD，再利用垂心的 3 性质，垂直关系的向量表示，二倍角的正切公式计算得解.    【详解】在V ABC 中，取AB的中点D，连接HD，则HAHB 2HD，如图， 第2页/共22页 学科网（北京）股份有限公司     2   4  7 由2HA2HB3HC 0，得CH  (HAHB) HD，于是CD  HD， 3 3 3    7       CACDDA HDDA,HB  HDDB  HDDA， 3         由H 是V ABC 的垂心，得HDDA,HBCA，则HDDA0,HBCA0   7    7 2  2  21  因此CAHB ( HDDA)(HDDA) HD DA 0，即|DA| |HD|， 3 3 3  | AD| 21 显然tanAHD   ，BHDAHD ，令直线BH 交AC于F ，AH 交BC于E， |HD| 3 π 在RtACE,RtAHF 中，ACBCAE  AHF CAE，即ACBAHF， 2 21 2 2tanAHD 3 21 则tanACB tan(π2AHD) tan2AHD   ， 1tan2AHD 21 2 1( )2 3 21 所以tanC的值为 . 2 故选：B 【点睛】关键点睛：涉及向量垂直关系，利用基底表示出相关向量，再利用向量数量积的运算律求解是关 键. π 2π  5. 已知  π，0π，sin   cos．若tan3k，tan3k，则k （ ） 6  3  1 1 3 3 A.  B. C.  D. 2 2 2 2 【答案】B 【解析】 π 【分析】根据题意分析可得 ，利用两角和差公式结合指数幂运算求解. 6 π π   π   π 【详解】由题意可得cossin     cos   cos   ， 2 6  6   6 π π 5π 因为  π，0π，则0  ， 6 6 6 π π 可得 ，即 ， 6 6 第3页/共22页 学科网（北京）股份有限公司π tantan 3k 3k 3k 3k 3 则tan tan     ， 6 1tantan 13k3k 2 3 令t 3k 0， 1 t 3 则 t 3 ，整理得 3t2 2t 3 0，解得t  3或t   （舍去），  3 2 3 1 即3k  3，解得k  ． 2 故选：B．  1    6. 在V ABC中，BD  BC ，E是线段AD上的动点（与端点不重合），设CE  xCA yCB，则 3 2x3yxy 的最小值是（ ） xy A.10 B.4 C.7 D.13 【答案】D 【解析】 3 【 分 析 】 由 已 知 条 件 结 合 平 面 向 量 基 本 定 理 可 得 x y 1 ， x0,y0 ， 则 2 2x3yxy 2 3 2 3  3    1   x y 1，化简后利用基本不等式可得答案. xy y x y x  2   1  3 【详解】因为BD  BC ，所以CB CD， 3 2      3  因为CE  xCA yCB，所以CE  xCA yCD， 2 3 因为A,D,E三点共线，所以x y 1，x0,y0， 2 2x3yxy 2 3 2 3  3    1   x y 1 xy y x y x  2  2x 9y 2x 9y 2x 9y  33 17  72  13 ， y 2x y 2x y 2x 2x 9y  1    x  y 2x  2 当且仅当 ，即 时取等.  x 3 y 1  y  1  2  3 第4页/共22页 学科网（北京）股份有限公司故选：D.        ab     7. 已知向量 a  b 4,ab 8,c  ，且 nc 1，则n与c夹角的最大值为（ ） 2 π π π 5π A. B. C. D. 6 4 3 12 【答案】A 【解析】   2π         【分析】先得到a,b的夹角为 ，设a4,0，b 2,2 3 ，故c  1, 3 ，设n x,y ，由 3     nc 1得到 x1 2   y 3 2 1，设x1cos,y  3sin，设n,c夹角为，表达出 4cos 3sin q 3 cos ，换元后得到cos  ，由对勾函数性质得到其值域，从而确定 2 2cos2 3sin5 4 4q  3  cos ,1，得到夹角最大值.  2      1 2π 【详解】因为ab  a  b cos，所以16cos8，解得cos ，故 ， 2 3   设a  4,0，b    2,2 3  ，则c   ab   1, 3  ， 2      设n x,y ，则nc x1,y 3 ， 则 n  c    x1 2  y 3 2 1，即 x1 2   y 3 2 1， 设x1cos,y  3sin，     nc x 3y 4cos 3sin 设n,c夹角为，则cos     ， n  c 2 x2  y2 2 2cos2 3sin5  π 令cos 3sint，则t 2sin   2,2  ，  6 4t q2 5 则cos ，令 2t5 q 1,3 ，则t  ， 2 2t5 2 第5页/共22页 学科网（北京）股份有限公司q2 5 4 则 4t 2 q23 q 3 ， cos     2 2t5 2q 4q 4 4q q 3 其中 y   在q1, 3上单调递减，在q 3,3上单调递增，     4 4q q 3 3 当q  3时， y   取得最小值，最小值为 ， 4 4q 2 q 3 当q 1或3时， y   取得最大值，最大值为1， 4 4q q 3  3  故cos   ,1， 4 4q  2   π 由于 y cos在  0,π  上单调递减，故 0, ，    6   π n与c夹角的最大值为 . 6 故选：A 【点睛】平面向量解决几何最值问题，通常有两种思路： ①形化，即用平面向量的几何意义将问题转化为平面几何中的最值或取值范围问题，然后根据平面图形的 特征直接进行求解； ②数化，即利用平面向量的坐标运算，把问题转化为代数中的函数最值与值域，不等式的解集，方程有解 等问题，然后利用函数，不等式，方程的有关知识进行求解.  1 8. 已知a0， f  x  aex  ln  xb  ，当x 0时， f x0，则a  1b 3的最大值为（ ）  x 1 2 A. B. e2 e2 3 4 C. D. 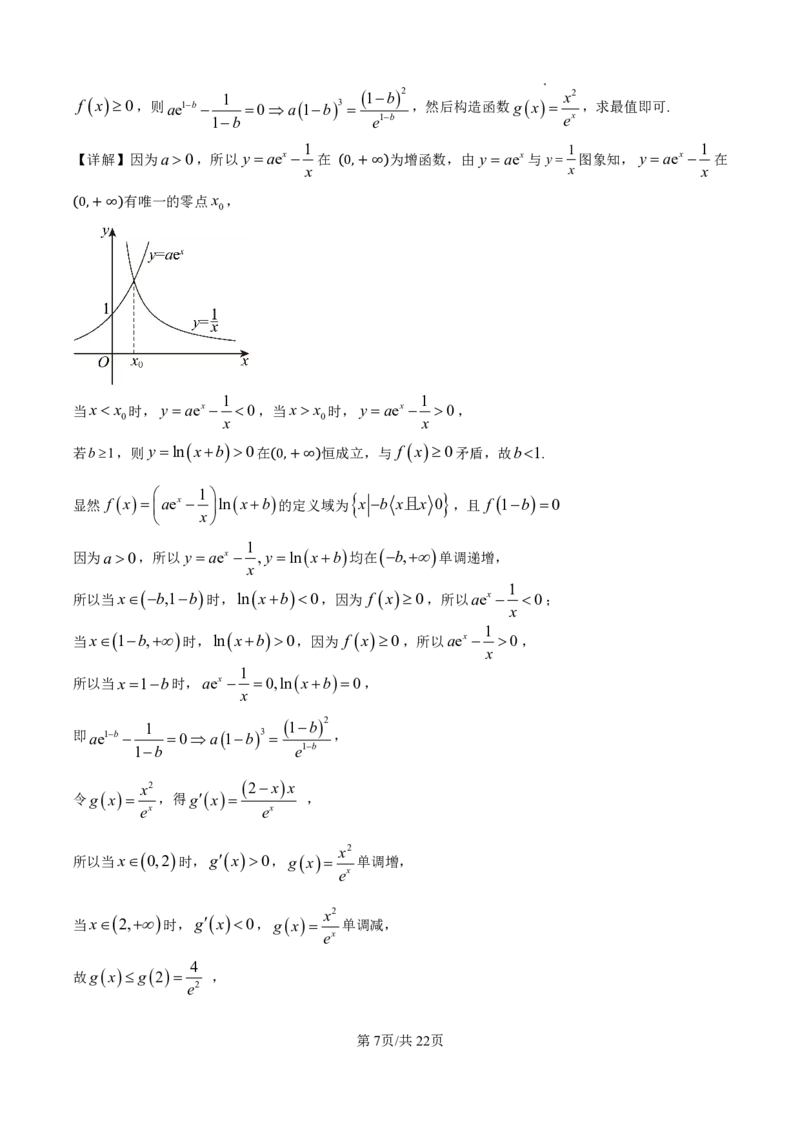e2 e2 【答案】D 【解析】 1 【分析】先分析得b1， f  1b 0， y aex  ,y ln  xb 均再 b, 单调递增；所以要使 x 第6页/共22页 学科网（北京）股份有限公司f  x 0，则ae1b  1 0a  1b 3   1b 2 ，然后构造函数g  x  x2 ，求最值即可. 1b e1b ex 1 1 1 【详解】因为a0，所以 y aex  在 为增函数，由 y  aex与y 图象知， y aex 在 x x x 0,+∞ 有唯一的零点x ， 0 0,+∞ 1 1 当x x 时， y aex 0，当x x 时， y aex  0， 0 0 x x 若b1，则 y ln  xb 0在 恒成立，与 f  x 0矛盾，故b1. 0,+∞ 显然 f  x   aex  1 ln  xb  的定义域为  x b x且x 0  ，且 f  1b 0  x 1 因为a0，所以 y aex  ,y ln  xb 均在 b, 单调递增， x 1 所以当xb,1b  时，ln  xb 0，因为 f  x 0，所以aex  0； x 1 当x 1b, 时，ln  xb 0，因为 f  x 0，所以aex  0， x 1 所以当x1b时，aex  0,ln  xb 0， x 1  1b 2 即ae1b  0a  1b 3  ， 1b e1b x2  2x  x 令g  x  ，得g x  ， ex ex 所以当x 0,2  时，g x 0，g  x  x2 单调增， ex 当x 2, 时，g x 0，g  x  x2 单调减， ex 4 故g  x  g  2  ， e2 第7页/共22页 学科网（北京）股份有限公司 1b 2 4 所以a  1b 3   ，当且仅当1b2即b1时等号成立； e1b e2 故选：D 【点睛】多变量问题通常需要先找到变量之间的关系，然后将多变量转化为单一变量，然后构造函数利用 导数求其最值即可. 二、多选题：本题共 3小题，每小题6 分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9. 对于函数 f  x  定义域中任意的x ,x  x  x  ，有如下结论，①  x x  f  x  f  x  0， 1 2 1 2 1 2 1 2  x x  f  x  f  x  ② f  x 2  f  2x 0，③ f  1 2   1 2 ，④ f  2x  f  22x 0.下列函数能 1 1 1 1  2  2 同时满足以上两个结论的有（ ） π  A. B. f  x sin x 2  =ln C. f  x ex D. f  x  x3 【答案】BCD 【解析】 【分析】先对四个结论进行解读，得出函数的单调性，奇偶性，周期性和凹凸性，对选项一一判断，即得 结果. 【详解】由①  x x  f  x  f  x   0可得，函数 f  x  在定义域内为增函数； 1 2 1 2 由② f  x 2  f  2x 0可得， f(x) f(x)0，即函数 f  x  为奇函数； 1 1  x x  f  x  f  x  由③ f  1 2   1 2 可得，函数 f  x  的图象向下凸.；  2  2 由④ f  2x  f  22x 0可得， f(x2)f(x)， 1 1 即 f(x4)f(x2) f(x) ，说明函数 f  x  的周期为4. 对于A，函数 f  x lnx不是奇函数，图象向上凸，也没有周期，故排除； 2π π  T   4 对于B, 函数 f  x sin x是奇函数，且周期为 π ,故符合要求； 2  2 第8页/共22页 学科网（北京）股份有限公司对于C，函数 f  x ex在R 上单调递增，且其图象向下凸，故符合要求； 对于D， f  x  x3是奇函数，且在R 上单调递增，故符合要求. 故选：BCD. 10. 已知复数z ，z ，z ，则下列说法中正确的有（ ） 1 2 3 1 3 1 3 A. 若z z  z z ，则z 0或z  z B. 若z   i，则z2024   i 1 2 1 3 1 2 3 1 2 2 1 2 2 C. 若z2 z2 0，则z  z 0 D. 若z z  z z ，则|z ||z | 1 2 1 2 1 1 2 2 1 2 【答案】ABD 【解析】 【分析】根据复数的运算法则可判断A；先计算z3 1，再求z2024，判断B；用特例验证C；利用zz  z 2 1 1 说明D正确. 【详解】对于A，z z  z z  z (z z ) 0 z  0或z  z ，故A正确． 1 2 1 3 1 2 3 1 2 3 1 3 1 3 对于B，方法：z2   i，z3 1，z4   i，所以zn以3为周期，所以 1 2 2 1 1 2 2 1 1 3 z2024  z36742  z2   i，故B正确． 1 1 1 2 2 2π 2π 2π 方法二（复数的三角表示）：z cos isin ，所以z 的模为1，辐角为 ，则z2024的模为1，辐 1 3 3 1 3 1 2π 4π 角为 20242π674 ， 3 3 4π 4π 1 3 所以z2024 cos isin   i．故B正确． 1 3 3 2 2 对于C，取z 1，z i，则z2 z2 0，此时z  z ，故C错误． 1 2 1 2 1 2 对于D，z z |z |2，z z |z |2，所以z z  z z |z ||z |，故D正确． 1 1 1 2 2 2 1 1 2 2 1 2 故选：ABD 11. 已知函数 f  x 2sinxcosx2sin2x1  N*  在   π , π 上有最大值，无最小值，则（ ） 12 3 第9页/共22页 学科网（北京）股份有限公司  A. f x 为奇函数 π π   B. f x 在 , 上单调递增 4 2 π C. x 是 f  x  离 y 轴距离最近的对称轴 8 D. f  x  的最小正周期为π 【答案】CD 【解析】 【分析】首先化简函数 f  x  的解析式，根据函数的形状，确定端点的取值范围，即可求的值，再根据函 数的性质，判断选项. 【详解】 f  x sin2x  cos2xsin2x  sin2xcos2x 2sin  2x π .  4  π π π π π 2π π 当x  , 时，2x    ,  ， 12 3 4  6 4 3 4  π π   因为函数 f x 在 , 上有最大值，无最小值， 12 3 π π π π 2π π 3π 所以存在kZ，使得 2kπ    2kπ    2kπ 2 6 4 2 3 4 2  9 3  9 3  12k  12k      2 2  2 2 3 3 整理得 ，kZ，所以 ，解得  .  3 15  3 15 8 2 3k  3k  8 8 8 8  π 又因为N*，故1，得 f  x  2sin2x ，  4 A. f 010，所以函数 f  x  不是奇函数，故A错误； π π π 3π 5π π 3π π π B.当x  , 时，2x   ,    , ，所以函数 f  x  在 , 上单调递减，故B错误； 4 2 4  4 4  2 2  4 2 π π π kπ π C.令2x  kπ，kZ，则x   ，kZ，所以离 y 轴距离最近的对称轴方程为x ，故C 4 2 8 2 8 正确； 2π D. f  x  的最小正周期为 π，故D正确. 2 第10页/共22页 学科网（北京）股份有限公司故选：CD 三、填空题：本题共 3小题，每小题 5分，共 15分. 3 12. 已知V ABC 的内角A,B,C 的对边分别为a,b,c，若a 2,b1,△ABC 的面积为 ，则c ______． 2 【答案】 3或 7 【解析】 π 2π 【分析】先由三角形的面积公式结合特殊角的三角函数值求出C  或 ，再由余弦定理求出结果即可； 3 3 3 【详解】a 2,b1,△ABC 的面积为 ， 2 1 1 3 3 所以 absinC = 创2 1�sinC ，解得sinC  ， 2 2 2 2 π 2π 因为0C  π，所以C  或 ， 3 3 π 当C  时，由余弦定理可得c2 a2 b2 2abcosC 4123，即c 3， 3 2π 当C  时，由余弦定理可得c2 = a2 +b2 -2abcosC = 4+1+2=7，即c 7， 3 综上c 3 或 7 ， 故答案为： 3或 7 . π 13. 在平面直角坐标系xOy中，一动点从点M ( 3,0)开始，以 rad/s的角速度逆时针绕坐标原点O做匀 0 2 1 3 速圆周运动，xs后到达点M 的位置.设A( , )，记(x)| AM |2，则(x)的单调递增区间为 2 2 _______________  2 8 【答案】 4k ,4k  kZ     3 3 【解析】 【分析】根据给定条件，利用三角函数的定义求出点M 的坐标，求出(x)并利用差角的余弦化简，再求 (x)的单调递增区间即可. π π π 【详解】依题意，xs后，动点走过的弧度数为 x，则M( 3cos x, 3sin x)， 2 2 2 第11页/共22页 学科网（北京）股份有限公司1 3 又A( , )， 2 2 π 1 π 3 则(x)( 3cos x )2 ( 3sin x )2 2 2 2 2 π π 4 3cos x3sin x 2 2 π π 42 3cos( x )， 2 3 π π (x)的单调递增区间，即y cos( x )的递减区间， 2 3 π π  2 8 则 2kπ x 2kππ  kZ ，即x 4k ,4k  kZ  ，   2 3  3 3  2 8 所以(x)的单调递增区间为 4k ,4k  kZ  .    3 3 14. 已知数列  a  满足a a,a  1 a2 2  n1,2,3, ，则 n 1 n1 2 n ①当a1时，存在kN*，使得a 2： k ②当a 1时，  a  为递增数列，且a 2恒成立； n n   ③存在aR，使得 a 中既有最大值，又有最小值； n 1 ④对任意的aR，存在n N*，当nn 时， a 2  恒成立. 0 0 n 2024 其中，所有正确结论的序号为______. 【答案】②③④ 【解析】 n1 1 【分析】对于①②，根据数列递推式，求出a2 43  ，结合题意，即可判断；对于③，举出特例， n 2 即可判断；对于④，分a 2和a 2情况讨论，结合数列的项的变化情况，即可判断. 1 1 1 【详解】对于①，由于a a,a  a2 2  n1,2,3, ，故a 0,n1， 1 n1 2 n n1 则a2  1 a2 2，则a2 4 1 a2 4  ，结合a1， n1 2 n n1 2 n 第12页/共22页 学科网（北京）股份有限公司则  a2 4  是以a2 43为首项，公比为 1 的等比数列， n 1 2 n1 n1 1 1 则a2 43   ,a2 43   ， n 2 n 2 n1 n1 1 1 令a2 43   4，则3   0，n不存在， n 2 2 故不存在kN*，使得a 2，①错误； k 对于②，当a 1时，由①知，  a2 4  是以a2 43为首项，公比为 1 的等比数列， n 1 2 n1 n1 1 1 则a2 43   ,a2 43   ， n 2 n 2 n n1 n 1 1 1 则a n 2 1 a n 2 43 2   43 2   3 2   0 ，得a n 2 1 a n 2， n1 故  a n  为递增数列，而a n 2 43    1 2    4，故a n 2恒成立，②正确； 1 对于③，当a 2时，当n1时，a  a2 2 2， 1 n1 2 n   此时 a 中有最大值2，有最小值为-2， n   即存在aR，使得 a 中既有最大值，又有最小值，③正确； n 对于④，由①知，a2 4 1 a2 4  ， n1 2 n 1 当a 2时，当n1时，a  a2 2 2，符合题意； 1 n1 2 n n1 当a 1 2时，a n 2   a2 4      1 2    4，随着n，a n 2 4， 1 又a 0,n1，则a 2，则必存在n N*，当nn 时， a 2  恒成立 n1 n 0 0 n 2024 1 综合以上对任意的aR，存在n N*，当nn 时， a 2  恒成立，④正确， 0 0 n 2024 故选：②③④ 四.解答题：本题共 5小题.解答应写出文字说明、证明过程或演算步骤. 第13页/共22页 学科网（北京）股份有限公司15. 在V ABC 中，角A,B,C .所对的边分别为a,b,c.已知  2ba  cosC ccosA. （1）求C； 3 （2）若V ABC 的内切圆半径为 ,c4，求V ABC 的面积. 2 π 【答案】（1）C  3 11 3 （2） 4 【解析】 【分析】（1）法一：利用正弦定理，将边化为角，再结合三角函数恒等变换，即可化简求角； 法二：利用余弦定理，将余弦化为边，再根据余弦定理，即可求角； （2）首先根据余弦定理化简得到 (ab)2 163ab ，再结合内切圆半径，集合等面积公式，得到 ab4ab，两式化简得到ab，即可求面积. 【小问1详解】 法—：因为  2ba  cosC ccosA，由正弦定理得， 2sinBcosCsinAcosC cosAsinC， 2sinBcosC sinAcosCcosAsinC， 即2sinBcosC sin  AC ， 又ABCπ，所以sin  AC sinB0， 1 π 所以cosC  ，又0C  π，即C  . 2 3 法二：因为  2ba  cosC ccosA，由余弦定理得 a2 b2 c2 b2 c2 a2 a2 b2 c2  2ba  c   2ba  b2c2a2 2ab 2bc a a2 b2 c2 a2 b2 c2 2b a2 b2 c2 b2 c2 a2 2b 2b2 a a a2 b2 c2 a2 b2 c2 1 b  a 2ab 2 1 π 所以cosC  ，又0C  π，即C  . 2 3 第14页/共22页 学科网（北京）股份有限公司【小问2详解】 由余弦定理得c2 a2 b2 2abcosC a2 b2 ab16，即(ab)2 163ab① 1 1 设V ABC 的内切圆半径为r ，由等面积公式得  abc  r  absinC . 2 2 1 3 1 3 即  abc   ab . 2 2 2 2 整理得ab4ab，即abab4(ab)2 a2b28ab16 ② 联立①②，解得ab11， 1 1 3 11 3 所以V ABC 的面积为 absinC  11  . 2 2 2 4 π π π π 2π 16. 已知函数 f(x)sin(x)在区间( , )单调，其中为正整数，|| ，且 f( ) f( ). 6 2 2 2 3 （1）求y f(x)图象的一条对称轴； π 3 （2）若 f( ) ，求 . 6 2 7π 【答案】（1）x  12 π （2） 3 【解析】 2π π 2π π 2π 【分析】（1）由正弦函数的单调性与周期性,可得T  ，所以 , 在同一个周期内，由 f    f  ， 3 2 3 2  3    取其中点值，即可得 f x 图象的一条对称轴； 2π 2π （2）由T   ，可得3，又为正整数，所以1，2，3，再分三种情况讨论，结合 f  x  在  3 7π x 处取得最值，即可求解. 12 【小问1详解】 π π 因为函数 f  x sin x 在区间 , 单调， 6 2 T π π 2π    ，T  ， 2 2 6 3 第15页/共22页 学科网（北京）股份有限公司π 2π  , 在同一个周期内， 2 3 π 2π  f    f  ， 2  3  π 2π  y f  x  图像的一条对称轴为 2 3 7π x  2 12 【小问2详解】 2π 2π 由（1）知，T   ，即3，  3 又为正整数，所以1，2，3， 7π 由（1）知， f  x  在x 处取得最值， 12 7π π π 7π 所以  kπ，kZ，即  kπ，kZ． 12 2 2 12 π π π  π  当1时， kπ，kZ，由 ，知 ，所以 f  x sinx ， 12 2 12  12 π  π π  π 3 所以 f   sin   sin  ，不符合题意； 6 6 12 12 2 2π 当2时， kπ，kZ， 3 π π  π 由 ，知 ，所以 f  x sin2x ， 2 3  3 π  π π 2π 3 所以 f   sin2   sin  ，符合题意； 6  6 3 3 2 5π 当3时， kπ，kZ， 4 π π  π 由 ， ，所以 f  x sin3x ， 2 4  4 π  π π 2 3 所以 f   sin3     ，不符合题意， 6  6 4 2 2 π 综上所述， . 3 1  a n,n为奇数, 17. 设S 是数列  a  的前n项和，已知a 1，a 2 n n n 1 n1  a 2n,n为偶数. n 第16页/共22页 学科网（北京）股份有限公司（1）证明：  a 2  是等比数列； 2n （2）求满足S 0的所有正整数n. 2n 【答案】（1）证明见解析 （2）正整数n为1，2 【解析】 【分析】（1）由定义能证明数列  a 2  是等比数列； 2n n1 n 1 1 1 （2）由a 2    ，得a a 84n3   ，从而 2n 2 2 2n1 2n 2 2 n  3 3 1 S  a a  a a  a a 2n   3   ； 2n 1 2 3 4 2n1 2n  2 2 2 由求和式子由此能求出满足S 0的所有正整数n的值． 2n 【小问1详解】 1 1 1 由已知得a  a 2n1  a 4n 2n1 a 1， 2n2 2 2n1 2 2n 2 2n 1 所以a 2  a 2 ， 2n2 2 2n 3 1 其中a  ，a 2 0， 2 2 2 2 1 1 所以  a 2  是以 为首项， 为公比的等比数列； 2n 2 2 【小问2详解】 n1 1 1 由（1）知a 2    ， 2n 2 2 n 1 所以a    2， 2n 2 n1 1 a 64n   ， 2n1 2 n 1 所以a a 84n3   ， 2n1 2n 2 所以S  a a  a a  a a  2n 1 2 3 4 2n1 2n 第17页/共22页 学科网（北京）股份有限公司 2 n n 1 1 1 1 8n4  12n 3       2n26n33    2 2 2  2 2 n  3 3 1 2n   3   ，  2 2 2 当n2时，  S  单调递减，其中S  5 ，S  7 ，S  21 ， 2n 2 2 4 4 6 8 所以满足S 0的所有正整数n为1，2. 2n x e 18. 已知函数 f  x 2cos2  1,x 0,2π  . 2 ex   （1）证明： f x 的导函数有且仅有一个极值点；   （2）证明： f x 的所有零点之和大于2π. 【答案】（1）证明见解析   （2） f x 的所有零点之和大于2π，理由见解析. 【解析】 【分析】（1）要确定 f x  的极值点情况，则需要判断其导函数的单调性，设g  x  f x  ，对g x  进 行变形处理，即g x e1x  1ex1cosx  ，即判断函数h  x 1ex1cosx的取值情况，即可得g x  的 取值情况，从而确定函数 f x  的极值点取值个数； （2）结合 f x  的单调性，确定其零点，从而得函数 f  x  的极值点分布，根据函数 f  x  单调性结合零     点存在定理即可确定函数 f x 的零点个数及范围，利用三角函数与指数函数的单调性即可判断 f x 的所 有零点之和与2π的大小关系. 【小问1详解】 x e 因为 f  x 2cos2  1cosxe1x,x 0,2π ， 2 ex 所以 f x e1x sinx 设g  x  f x e1x sinx，x 0,2π  ， 所以g x e1x cosxe1x  1ex1cosx  ，其中e1x 0恒成立， 令h  x 1ex1cosx，x 0,2π  ， 第18页/共22页 学科网（北京）股份有限公司 π 则h x ex1cosxex1sinx 2ex1sinx ，  4 π  π 7π 因为x 0,2π  ，所以x    , ， 4  4 4   π 所以当x 0, 时，h x 0，函数h  x  单调递减，  4 π 5π 当x  , 时，h x 0，函数h  x  单调递增， 4 4  5π  当x  ,2π时，h x 0，函数h  x  单调递增；  4  又h  0 1e1 0,h   π  1 2 e π 4 1 1 2 e0 0 ，h   5π  h   π  0， 4 2 2  4   4 h   7π  1 2 e 7 4 π1 1 2 e10 ，h  2π h   7π  0  4  2 2  4  5π 7π 所以x   , ，使得h  x 1ex 0 1cosx 0 ，即e1x 0 cosx ， 0  4 4  0 0 0 故对于g x e1xh  x  有gx 0，当x 0,x  时，g x 0，函数 f x  单调递增，当x x ,2π  0 0 0 0 时，g x 0，函数 f x  单调递减， 0 所以x 是函数 f x  的极大值点， f x  无极小值点，故 f x  有且仅有一个极值点. 0 【小问2详解】 5π 7π 因为函数 f  x e1x cosx,x 0,2π  ，其导函数 f x e1x sinx，x   , ，使得当 0  4 4  x 0,x  时， f x  单调递增，当x x ,2π  时，函数 f x  单调递减， 0 0 又e1x 0 cosx ， 0  π 所以 f 0 e0, f x e1x 0 sinx cosx sinx  2sinx  ， 0 0 0 0  0 4 5 7  π 3π  因为x   π, π，所以x    ,2π，所以 f x 0， 0 4 4  0 4  2  0 第19页/共22页 学科网（北京）股份有限公司又 f 2π e12π 0， 故x  0,x  ，使得 f x 0，x  x ,2π  ，使得 f x 0，于是可得： 1 0 1 2 0 2 当x 0,x  时，fx0，f  x  单调递减，当x x ,x  时，fx0，f  x  单调递增，当x x ,2π  1 1 2 2 时， fx0， f  x  单调递减， 又 f π e1π 0, f   3π  e 1 3 2 π 10，故x   π, 3π ，  2  1  2  则 f   π  e 1 π 2 0, f  π e1π 10，所以存在   π ,π  使得 f 0， 2 2  所以 f  x  f  π 0，又 f  3π   e 1 3 2 π 0，所以 f  x  f   3π  0，则存在  π, 3π 使得 1  2  2  2   2  f 0， 又 f  2π e12π 10，所以函数 f  x  在区间x x ,2π  上无零点； 2 π 3π 故函数在x 0,2π  上有两个零点,，且 π ， 2 2 由 f  f 0可得： e1cos0,e1cos0 ，所以cose1,cose1， 又11e1e1e1e1， 所以coscoscos  2π ， π 3π π π 根据 π ，可得：  π， 2π π， 2 2 2 2 π  并且函数 y cosx在 ,π上单调递减，所以2π，即2π， 2    故 f x 的两个零点之和大于2π 【点睛】关键点睛：本题考查函数的极值点、零点与导数的关系，涉及到三角函数与指数函数混合运算， 难度较大.解决本题中证明极值点个数问题的关键是，将指数函数与三角函数的加减运算，变形成乘除运算， 这样避免求导数过程中，导函数的零点无法解含指数与三角函数的方程问题，例如本题中对函数 g x e1x cosx直接求其导数无法消除指数运算，将其转化为g x e1x  1ex1cosx  ，其影响正 第20页/共22页 学科网（北京）股份有限公司负的部分1ex1cosx的导函数零点可求，其单调性与极值点即可确定；解决本题中原函数零点之和的问题 π 3π 的关键是确定零点范围为 π 之后，结合零点所满足的等式关系 2 2 e1cos0,e1cos0 ，根据指数函数比较大小，利用诱导公式转化并结合余弦函数y cosx在 π   ,π上的单调性，即可确定零点之和与2π的大小关系. 2  19. 定理：如果函数 f (x)在闭区间[a，b]上的图象是连续不断的曲线，在开区间(a,b)内每一点存在导数， 且 f(a) f(b)，那么在区间(a,b)内至少存在一点c，使得 f(c)0，这是以法国数学家米歇尔罗尔的 名字命名的一个重要定理，称之为罗尔定理，其在数学和物理上有着广泛的应用. （1）设 f(x) x(x1)(x2)(x4)，记 f (x)的导数为 f(x)，试用上述定理，说明方程 f(x)0根的 个数，并指出它们所在的区间； （2）如果 f (x)在闭区间[a，b]上的图象是连续不断的曲线，且在开区间(a,b)内每一点存在导数，记 f (x) 的导数为 f(x)，试用上述定理证明：在开区间(a,b)内至少存在一点c，使得 f(b) f(a) f(c)(ba)； ab （3）利用（2）中的结论，证明：当0ab时， (ab)e 2 aea beb.（e为自然对数的底数） 【答案】（1）答案见解析； （2）证明见解析； （3）证明见解析； 【解析】 【分析】（1）注意到 f(0) f  1  f  2  f  4 0，结合罗尔定理可得答案； f  b  f  a  （2）构造函数F  x  f  x  f  a   xa ，后利用罗尔定理可证明结论； ba ab ab ab ab ab （3）注意到(ab)e 2 aea beb beb  e 2  e 2 aea ，后由（2）中结论可证明. 2 2 【小问1详解】 注意到 f(0) f  1  f  2  f  4 0，则由罗尔定理， 在(0,1)内存在x，使 f(x ) 0；在(1,2)内存在x ，使 f(x )0；在(2,4)内存在x ，使 f(x )0. 1 1 2 2 3 3 综上， f(x)0的根有3个，且分别位于(0,1)，(1,2)，(2,4)这三个区间内； 【小问2详解】 第21页/共22页 学科网（北京）股份有限公司f  b  f  a  ）证明：构造函数F  x  f  x  f  a   xa ， ba f  b  f  a  则F x  f  x  .注意到F  a F  b 0，由罗尔定理， ba f  b  f  a  则在(a,b)上至少存在一点c，使F c  f  c   0 ba f  b  f  a   f c  ，即在开区间(a,b)内至少存在一点c， ba 使得 f(b) f(a) f(c)(ba)； 【小问3详解】 ab 证明：当0ab时， 0a b. 2 由（2），因函数gx xex为R上连续函数，g x  x1  ex . ab ab 又a ， 则在(a, )上存在t ， 1 2 2 ab ab  ab ba 使g  g  a  g t   a  eab aea  1t  et 1  ；  2  1  2  2 1 2 ab ab 又 b，则在( ,b)上存在t 2 2 2 ab  ab ab ba 使g  b g   g t  b   beb  eab  1t  et 2  .  2  2  2  2 2 2 又令h  x  x1  ex h x  x2  ex，当x 0时，h x  x2  ex 0， 则h  x  在(0,)上单调递增， ba ba 又t t h  t h  t  1t  et 2   1t  et 1  . 2 1 2 1 2 2 1 2 ab ab ab ab ab 则beb  e 2  e 2  aea (ab)e 2 aea beb. 2 2 【点睛】关键点睛：本题关键为理解题干信息罗尔定理，第一问为定理的直接运用；第二问关键在与由所 需证明结构构造出相应函数； 第三问关键为对所需证明结构变形，使之能够利用第二问的结论. 第22页/共22页 学科网（北京）股份有限公司