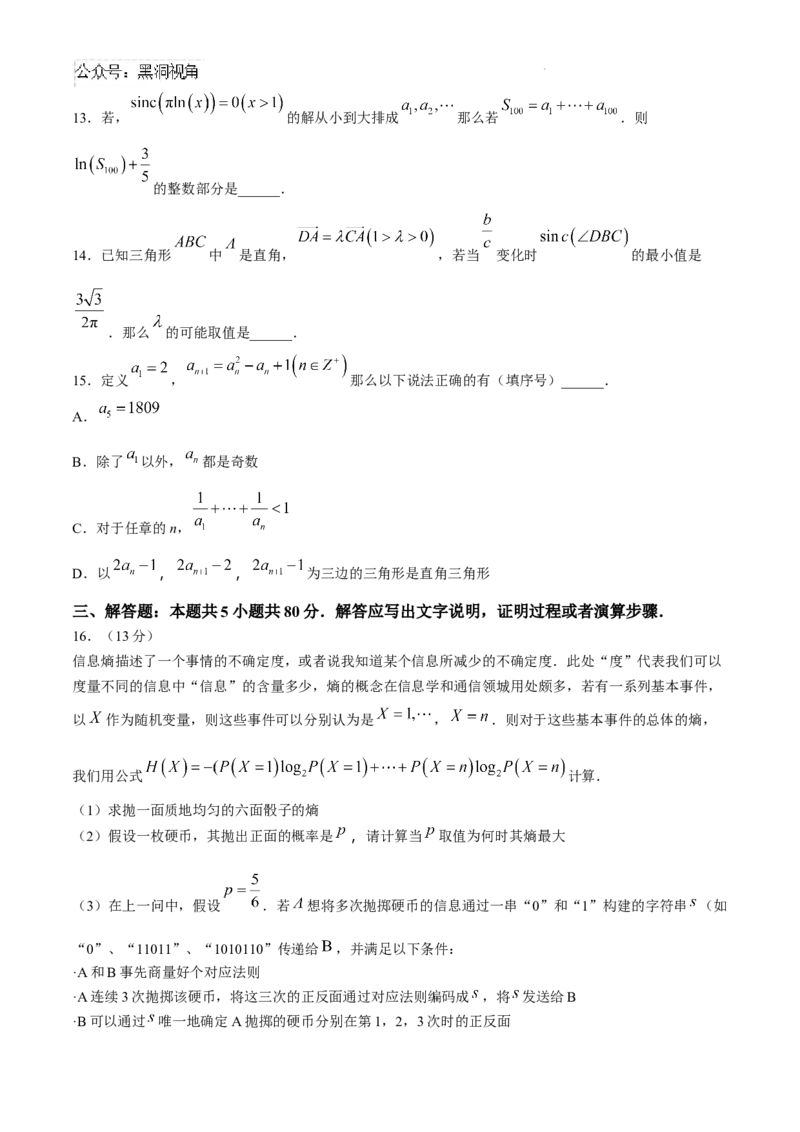文档内容
第二次天枢杯线上联考一试
数学
本试卷共5页,20题.全卷满分150分,考试用时120分钟,
注意事项:
1.填空题,主观题请自备答题纸.并将答案提交到对应的答题区.请保持字迹工整.笔记清
晰.字迹不清,提交错误的作答视为无效.
2.考试期间,请考生独立作答,禁止考生查网书籍、使用计算器等辅助工具、或在考试期间
与他人交流.试卷在考试期间禁止外传,考试结束后可以外传,但最好留下作者名称
skyhgzsh.
3.请使用高中课内知识答题,课外“超钢”知识请在答题纸上给出相应定理的证明,如果题
目中不涉及复数的相关内容,则默认范围为实数.自然数默认包含,正整数用 表示,不建
议使用如“趋近于,足够大”等模棚性词语
4.考试结束后.请在规定时间内以雨课堂或QQ私信(QQ:10691923)的途径,将答题纸
以电子版,照片或扫描的方式在府课章的相应位置处提交,未在规定时间内发送的卷子视为
未提交,不计人成绩.
5.本比赛的最终解释权归作者所有.考试期间如对试卷内容等方面有问题,请先通读试题内
容,如仍有疑间,请私信作者.
6.题目顺序不代表难度,部分题目可能难度较高!
7.已知:若 均为非负实数,则 .取等当且仅当
一、选择题:本题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知:哥德巴赫猜想认为任一大于2的偶数都可写成两个质数之和.定义 为全体素数的集合,那么
以下形式化命题中和哥德巴赫猜想不等价的是( )
A. , , ,
B.
C.
D. 或
2.设复数 , .那么如下说法中错误的是( )
学科网(北京)股份有限公司A. B. 在第二象限
C.若 ,那么 D.
3.称数列 和 “同增减”,如果 , 那么以下说法中正确的是(
)
A.两个单调递增数列 和 是同增减的
B. 和任意数列 有 和 同增减
C. 和任意数列 有 和 同增减
D. 和任意正数数列 有 和 同增减
4.已知平面上四个点 ,其中任意三个不共线.若 ,则直线 一定经过三
角形 的( )
A.外心 B.内心 C.重心 D.垂心
5.已知椭圆 过点 ,其右顶点 ,上顶点 .那么以下说法
正确的是( )
A.设 是半焦距 到 的其中一个焦点的距离),那么必然有
B. 到直线 的距离 不是定值
C. 和 没有交点
D.三角形 面积的取值范围是
6.如下图所示,边长为 的正方体成周期性排列,在正方体的各个角以及每个面的中心有原子分布的晶
体结构,我们称之为面心立方结构. 和 等部分金属就属于这种结构.若将原子认为是如此分布的等
大实心球,使得最近的两个原子球恰好相切,那么一个边长为 的面心立方正方体品格内被原子球所占据
的部分的体积是( )
学科网(北京)股份有限公司A. B. C. D.
7.仍然考虑上面的图形,若要将这一个立方体上的14个点染上红黄蓝三种颜色,使得被一条线段连接的
两个点不能染上同一种色,那么不同染色方案的种数是(旋转和镜像对称后重合的视为同一种)( )
A.3 B.6 C.9 D.12
8.已知: , , ,那么 三者的关系是( )
A. B. C. D.
9.不是方程 的解的选项是( )
A. B. C. D.
10.我们称两个正整数 和 互素,当且仅当 和 的最大公因数是1,我们定义 是小于:
的正整数中和 互素的数的个数,例如 .是因为小于6的数中只有1与5和6互素.那么以下
说法错误的是( )
A.有无限多个正整数 使 B.有无限多个正整数 使
C. 的解只有1和2 D.对于任意正整数 ,都有 使得
二、填空题:本题共5小题.每小题6分,共30分
11.定义 .那么 在 上的取值范围是______.
12.已知在平面 上 和单位圆交于 那么 的可能取值是 函数的定义见
上)______.
学科网(北京)股份有限公司13.若, 的解从小到大排成 那么若 .则
的整数部分是______.
14.已知三角形 中 是直角, ,若当 变化时 的最小值是
.那么 的可能取值是______.
15.定义 , 那么以下说法正确的有(填序号)______.
A.
B.除了 以外, 都是奇数
C.对于任章的n,
D.以 , , 为三边的三角形是直角三角形
三、解答题:本题共5小题共80分.解答应写出文字说明,证明过程或者演算步骤.
16.(13分)
信息熵描述了一个事情的不确定度,或者说我知道某个信息所减少的不确定度.此处“度”代表我们可以
度量不同的信息中“信息”的含量多少,熵的概念在信息学和通信领城用处颇多,若有一系列基本事件,
以 作为随机变量,则这些事件可以分别认为是 , .则对于这些基本事件的总体的熵,
我们用公式 计算.
(1)求抛一面质地均匀的六面骰子的熵
(2)假设一枚硬币,其抛出正面的概率是 ,请计算当 取值为何时其熵最大
(3)在上一问中,假设 .若 想将多次抛掷硬币的信息通过一串“0”和“1”构建的字符串 (如
“0”、“11011”、“1010110”传递给 ,并满足以下条件:
·A和B事先商量好个对应法则
·A连续3次抛掷该硬币,将这三次的正反面通过对应法则编码成 ,将 发送给B
·B可以通过 唯一地确定A抛掷的硬币分别在第1,2,3次时的正反面
学科网(北京)股份有限公司· 的长度 的期望 尽量小.
例如, 可以直接用每一位的数表示那一次硬币抛掷的结果,如表:
正正正 111
正正反 110
正反正 101
反正正 011
正反反 100
反正反 010
反反正 001
反反反 000
从而显然无论如何.都有 成立.从而
请设计一种方案,使得:
(a)
(b)
并证明.(你不需要分别给出方案, 的方案自动满足
17.(13分)
已知一个平行六面体的最长体对角线长度是 ,证明:该平行六面体的体积 .并指出取等条件.
18.(17分)
我们定义 的函数使得在 上,
证明: 当且仅当
过程提示(若不按本过程,证明成功亦为满分):设 , , .
得到 关于 , 的表达式(提示: ,利用递推式得到矛盾,由此证明原命题.
19.(17分)
学科网(北京)股份有限公司已知 的两个焦点和两个顶点四点共圆,且 和 ,
均相切
(1)求 的表达式和离心率
(2)已知动点 在 的第一象限上运动, 和 相切,和 交于 ,和 交于 。设 右焦点为 ,
证明 是常量,并计算其正切值.
20.(20分)
设
(1)若 .求 的单调区间,并分析是何种单调.
(2)分析 的零点数量和 的关系.
第二次天枢杯线上联考一试数学答案
1.C
解答
A的意思是不存在偶数 是哥猜的反例
B的意思是两个质数的和作为集合包含了所有大于2的偶数的集合
C的意思是两个质数的和中不是偶数的部分为空,也就是两个质数的和都是偶数
D的意思是要么一个偶数不大于2,要么存在一个质数使得该偶数减去质数之后还是一个质数.
综上,只有C和哥猜无关,而且C实际上是错的,因为 是两个质数的和,但不是偶数,和命题矛
盾.
2.A
解答
A注意到 从而A错误
B注意到 , ,从而设 ,则
,从而在第二象限.B正确.
C代入就发现 ,从而C正确
学科网(北京)股份有限公司D化简就是 ,而后者是 ,从而两个都是有理数,差也是有理数.从而
D正确
从而答案是A.
3.B
解答
A注意到两个数列都是单调递增的,从而两个差都是正的,它们的积也是正数.A正确
B考虑 和 ,注意到其积是—1,和“同增减”矛盾.B正确.
C代入就发现积是 ,从而必然非负.C正确
D注意到 的时候 ,反之亦然.从而 从而D正确.
从而答案是B.
4.D
解答
首先,考虑 和 分别垂直直线 于 和 ,注意到题设等价于 ,也就是 重合,从
而 ,也就是 过三角形 的垂心.
从而答案是D.
5.C
解答通过带入,注意到 ,不妨设 , ,那么 ,
A注意到当 的时候 ,但是 ,从而A错误
B从而直线 是 ,计算 ,B错误.
C注意到 ,从而有 ,同理 .从而 ,和 没有交点.C正
确·
D注意到 ,从而 ,也就是1取不到,D错误
从而答案是C.
学科网(北京)股份有限公司6.B
解答题目创意和部分描述来自《暗杀教室》122话,有改动.
由图可得两个原子间最短距离是 ,从而球半径 ,带入公式得到一个球的体积是 .同时,
一个晶体内包含6个半球和8个 ,也就是4个球,从而总体积是 ,答案为B.
7.A
解答
我们首先假设正方体的一对对顶点是在 和 ,若将 染成 色,那么 ,
, 三个点必然都是 色,而 , , 必然都是 色.如此递推
可以恰好染完整个正方体.而当 色固定的时候通过旋转就可以得到 互换的正方体.从而只有三种不同
的方案,也就是将面的中间分别染上红黄蓝三种颜色.
8.C
解答先比较 和 ,注意到 , ,从而
再比较 和 ,注意到 ,而又有 .从而只需要证明 ,这是显然的,因为
有常用不等式 从而答案是C
9.B
解答注意到带入可以发现方程是 ,其中 是答案中的选项.
从而只有B带入发现符号相反,从而答案是B.
10.D
解答
A是因为对于任意的奇质数 ,有
B是因为对于任意的正整数 ,有
C是因为当 的时候1和 都和 互素,从而 至少是2
学科网(北京)股份有限公司D错误是因为 是无解的.因为显然对于任意的 .若 和 互素则 也和 互素,反
之亦然.而当 为偶数时自己和自己对应的 和 不互质.而 的时候 .从而该方程无
解.综上,D选项是错误的,从而选D
二、填空题:本题共5小题,每小题6分,共30分.
11.(0,1)
解答求导发现 ,而因为 ,从而分子为负,必然单调减少.又因为
它连续,所以只需要算端点取值即可,右侧 ,从而是左开0,极大值注意到以下放缩
,从而 ,也就是其取不到1但是可以无限接近.从而是右开1,
从而范围是
12.1
解答显然,注意到 从而 , .又因为可以证明这个交点满足
,从而 , ,从而
13.101
解答首先,解 就是解 并且 ,从而可以得到
,结合 可得 从而 ,取对数后就是
注意到
从而我们要证明
学科网(北京)股份有限公司我们把左边放大到 并证明其小于 ,注意到 ,而
(也可以是 )从而命题成立.也是整数部分是101.
14.
解答题目创意来自Antonio Caminha Muniz Neto的“An Excursion through Elementary Mathematics,
Volume II’”的第275页,有改动.
设 , ,那么
从而设 ,那么有
从而 ,
因为 , ,从而 , ,而
也就是 ,解出 ,也就是 ,带入得到
.因为取正,从而 ,此时注意到 仍然能取到,从
而答案就是 .
15.BCD
解答本题创意来自第15届大学生数学竞赛初赛A卷第六大题和OEIS的数列A000058
A就是计算: , , , .所以A错误
B注意到 显然都是整数,从而 必然是偶数,从而+1必然是奇数,B正确
学科网(北京)股份有限公司C首先可以注意到 ,从而 , ,从而 ,
从而可以证明 ,C正确.
D注意到 ,从而命题成立
从而答案是BCD.
三、解答题:本题共5小题,共80分.解答应写出文字说明、证明过程或者演算步骤.
16.解答第一问:因为六个面,每个面的概率都是 ,
从而
第二问:注意到 ,记录其为 ,
从而 , ,
从而有下表
— — —
0
1
从而 时熵最大.
第三问:
(a),我们的思路是尽量让更可能的事件用更短的 表示.从而考虑在例子的基础上作如下替换:11代
表三面正,100代表正正反,0001代表正反反,0000代表三面反.
从而有 的概率是 ,有 的概率是 .计算可得 .从而方案
满足要求.
(b),我们直接给出编码:
正正正 1
正正反 011
学科网(北京)股份有限公司正反正 010
反正正 001
正反反 00011
反正反 00010
反反正 00001
反反反 00000
计算可得 从而方案满足要求.
17.解答首先,设三个边是 ,那么对于任意的体对角线 ,
, ,
从而可以设 和 反向、 和 反向, 和 反向.则四个体对角线的平方和就是
的对应部分)+ 的对
应部分)
注意到 实际上等于0(因为正负相消),从而其他两个对
应部分也是0,四个体对角线的平方和就是
因为 是最长的,从而其不小于平均值(取等条件是四个都相等,也就是每个角都是直角,也就是它是
长方体),从而
而此时注意到 ,不妨设 是 对应的平面, 是 对应的高.那么 (取等条件是
)
而 本身作为垂线高,也有 (取等条件是 和平面垂直,也就是 , , ,从而
学科网(北京)股份有限公司注意到
,从而 (此处三边相等的时候取等)取等条件是该平行六面体就
是立方体.
18.解答本题源自《数学天书中的证明》第五版
首先,显然 , , .
注意到 ,从而
也就是 .因为 , .若 ,
其中 是大于1的奇数
递归初始有 不是 的倍数.
若 , 不是 的倍数,那么 不是 的倍数,
而 是.从而 也不是 的倍数.
从而 总不是 的倍数,从而总不是 的倍数.
若 (其中 是整数),那么 ,从而 .
但是 不是 的倍数,从而 不是整数, 更不可能是1,矛盾
若 , ,
定义 而初始有 是奇数
若 是奇数,那么 是偶数和奇数的和,从而是奇数
学科网(北京)股份有限公司从而 当 时总是奇数.
如上,类似地有 ,但是 是奇数除以偶数,从而必然不是整数,矛盾.综
上,命题成立.
19.第一问:首先,注意到焦点和长轴顶点贡献,从而不会共圆.从而焦点和短轴顶点共圆.
因为焦点到短轴顶点的距离就是 ,结合对角互补,可得它们实际上构成了一个正方形,从而 ,
也就是 ,从而 ,代入 ,也就是 恰好有
一个解,也就是 , .
也就是 , .
从而斜率 必然存在且非0,设切线
第二问:设
得到
代入
因为 在 上,从而 ,从而 .
因为解只有 ,从而第二个因素的解也是 ,也就会 ,或者说是 ,
从而 ,也就是
联立 和 ,解出 ,
同理有
从而 , ,
学科网(北京)股份有限公司, ,
注意到因为 ,从而 .从而写出所求角度 的正切值表达式.
(1)
(2)
(3)
(4)
先处理分子:
再处理分母:
当 时候注意到能解出 ,此时 和 重合,与它们只有交点相矛盾.而 不可能是
0.
从而 ,又注意到通过画图可知该角度在 变化的时候 恒为锐角,从而其
是定角.
20.解答第一问:
在本问中
.
注意到 ,从而 的正负只和 有关,从而可作出下表:
学科网(北京)股份有限公司+ 0 — 0 +
从而 的单调递增区间是 ,单调递减区间是 .
第二问:
时注意到 恒成立,从而没有零点.
时,注意到所求可以化为 的解的数量.而此时若设 ,
,则 , 从而可以作下图:
0
+ + + 0 — —
0 0
0 1
— — 0 + + +
0 0
当 时,注意到 ,注意到 ,
从而 单调递增,零点若有则至多有一个.
注意到设 时有 , ,从而
学科网(北京)股份有限公司设 时有 ,从而 从而在 上必然有一个零点.从
而总是有一个零点. 时候,我们考虑 ,注意到 ,从而可作出下表:
1
0 — 0 + + +
1
从而其在 之间有一个零点,设其为 ,从而考虑 ,
其在 上的正负性和 一样,从而 先单调减少后单调递增,
其极小值点就是最小值点,在 处取到.
注意到 ,从而此处 ,
从而当 时 的最小值比0大,此时没有零点;
当 时 的最小值恰好就是0,从而只有一个零点;
时 在 处小于0,在 时
当 ,
从而 上有一个零点.
注意到 时),当 时 ,从而在
时 ,从而在 上有一个零点.从而此时共有两个零点.
综上,当 时 没有零点,当 或者 时有一个零点;当 时有两个零点.
学科网(北京)股份有限公司