24届高三文科数学上期半期考试试卷答案(1)_2023年11月_0211月合集_2024届四川省成都市第七中学高三上学期期中考试_四川省成都市第七中学2024届高三上学期期中考试文科数学

2023——2024学年度高2024届半期考试
数学参考答案（文科）
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 B B B D C A A D B C A A
二、填空题
13. 14. 15. 2191 16.
9
三．解1答35题° ： 5 ②③
b 2sinB
17(Ⅰ) 4，根据正弦定理得 4,即sinB 2  1cosB  ，代入sin2 Bcos2 B 1，
1cosB 1cosB
即4  1cosB 2 1cos2 B   1cosB  1cosB  ,由于1cosB 0，即4  1cosB  1cosB，
3
解得cosB  .…………5分
5
a c 8
(Ⅱ)根据正弦定理得sin AsinC   1，即ac2，由(Ⅰ)知b .由余弦定理得
2 2 5
b2 a2 c2  公 2accosB   ac 2  16 ac 4 16 ac，解得ac  9 .…………10分
众 5 5 20
3 号
又因为cosB  ，所以
：
5
一
4 1 9
sinB  .S  acsinB  .…………12分 枚
5
ABC
2 50
试
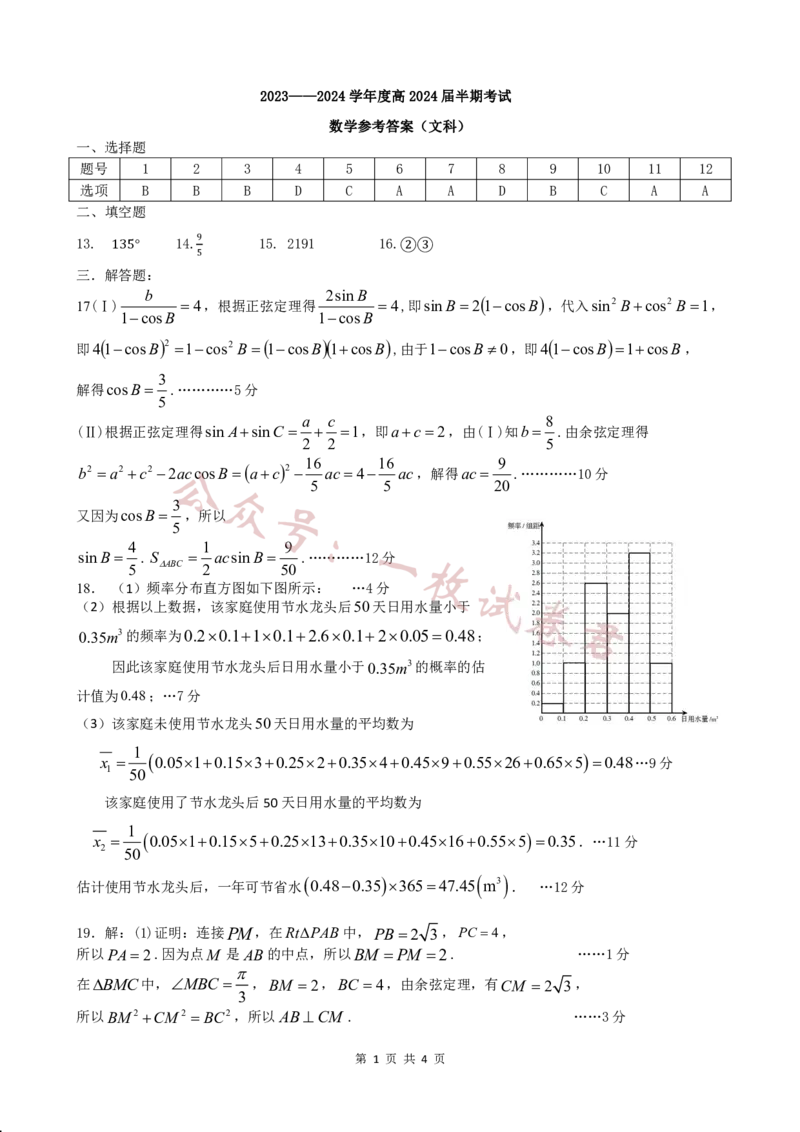
18． （1）频率分布直方图如下图所示： …4分
卷
（2）根据以上数据，该家庭使用节水龙头后50天日用水量小于
君
0.35m3的频率为0.20.110.12.60.120.050.48；
因此该家庭使用节水龙头后日用水量小于0.35m3的概率的估
计值为0.48；…7分
（3）该家庭未使用节水龙头50天日用水量的平均数为
1
x   0.0510.1530.2520.3540.4590.55260.655 0.48…9分
1 50
该家庭使用了节水龙头后50天日用水量的平均数为
1
x   0.0510.1550.25130.35100.45160.555 0.35．…11分
2 50
估计使用节水龙头后，一年可节省水  0.480.35 36547.45  m3  ． …12分
19．解：(1)证明：连接PM，在RtPAB中，PB2 3，PC 4，
所以PA2.因为点M 是AB的中点，所以BM PM 2. ……1分

在BMC中，MBC  ，BM 2，BC 4，由余弦定理，有CM 2 3，
3
所以BM2 CM2 BC2，所以ABCM . ……3分
第 1 页 共 4 页
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#}公
众
号
：
一
枚
试
卷
君
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#}2x2  a2  xa  2xa  x1 
21. 解：（1）F  x  x2 2xalnxax ，F x   ，·······1分
x x
∵F  x 的定义域为 0,．
a a
a0,则 0F(x)0,有x (舍去)，x1, ···················································2分
2 2
F

x
在
0,1
上递减，F 
x
在 1,上递增，
F  x  a1，F  x 无极大值．······································································4分
极小
sinx 12cosx
（2）设h  x ax x[0,2]，h x a ，·······················5分
2cosx  2cosx 2
12t 2  t2  t1  2  t1 
设t cosx ，则t1,1  ， t  ， t   ≥0 ，········7分
 2t 2  2t 4  2t 3
 1
∴
t

在
1,1  上递增，∴
t

的值域为

1,

，·······8分
 3
1
①当a≥ 时，h x ≥0，h  x  为  0, 上的增函数，∴h  x ≥h  0 0，适合条件．·······9分
3
  1
②当a≤0时，公∵h  a  0 ，∴不适合条件．·······10分
2众 2 2
1 号 sinx
③当0a 时，对于0 x ，h  x ax ，
：
3 2 3
一
sinx cosx  
令T  x ax ，T x a ，存在x 0,枚，使得x 0,x  时，T x 0，
0
3 3  2
试
∴T

x

在

0,x

上单调递减，∴T

x
T 
0
0，即在x
0,x

时卷，h

x
0，∴不适合条件．
0 0 0
君
1 
综上，a的取值范围为

, ．·······12分
3 
1
22．解：（1）消去参数t，得曲线C 的直角坐标方程为 y2  x1 ,即x2y30.
1
2
xcos
把 代入2 6sin，曲线C 的直角坐标方程为x2  y2 6y 0.…5分
y sin 2
|0233| 3
（2）圆心到直线AB的距离为d  
1+
2 2 5
3
圆上动点P到弦AB的距离的最大值为d+r  3
5
2
 3  12
解法1：弦长 AB 2 r2d2 2 32   
 5 5
1 1 12  3  18  
∴PAB的面积S的最大值为 AB d=    +3  1+ 5 . ………10分
2 2 5  5  5
解法2：设圆C 上动点P(3cos,33sin) ,P到直线C 的距离
2 1
3cos2(33sin)+3 6sin3cos3 3 5sin()3 3
d     3
5 5 5 5
第 3 页 共 4 页
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#} 2
x1 t

 5 x2  y2 6y 0 2
化C 的参数方程为 代入 得，t2  t70
1  1 5
y 2 t

 5
2
2  2 12
则t t  ,tt 7 则 AB  t t   t t 24tt    4(7)
1 2 1 2 1 2 1 2 1 2
5  5 5
1 1 12  3  18  
∴PAB的面积S的最大值为 AB d=    +3  1+ 5 .
2 2 5  5  5
2x2, x3

23.解：（1） f(x) f(x4)|x1||x3| 4, 3 x1 --------3分

2x2, x1
当x3时，2x28，解得x5； 当x1时，2x28，解得x3
综上，原不等式的解集为(,5][3,) ------------------5分
b b
（2）因为|a|1,|b|1，所以 f(ab)|ab1|1ab, |a| f( )|a|| 1||ba|
a a
公
b
令m f(ab)|a| f( 众)1ab|ba|， -------------7分
a
号
若ba，则m1ab|ba|(1a) ： (1b)，
一
b 枚
因为|a|1,|b|1，所以m0，所以 f(ab)|a| f( )； -------------9分
a 试
卷
若ba，则m1ab|ba|(1a)(1b)，
君
b b
因为|a|1,|b|1，所以m0，所以 f(ab)|a| f( )综上所述， f(ab)|a| f( ) ------------10分
a a
第 4 页 共 4 页
{#{QQABLYCUggigAhAAAAhCAw1wCEIQkBCCAIoOAEAMoAABgQNABAA=}#}