文档内容
2024—2025 学年度第一学期高二年级数学期中练习
一、选择题,共10小题,每小题4分,共40分.
的
1. 直线 倾斜角为( )
A. B. C. D.
2. 正方体 的棱长为a,则棱 到面 的距离为( )
A. B. a C. D.
在
3. 如图所示, 平行六面体ABCD﹣ABC D 中, ( )
1 1 1 1
A. B. C. D.
4. 已知直线 ,若 ,则 ( )
A. 或 B. C. 或 D.
5. 已知 为两条不同的直线, 为两个不同的平面,则下列结论正确的是( )
.
A 若 ,则
B. 若 ,则
C. 若 ,则
.
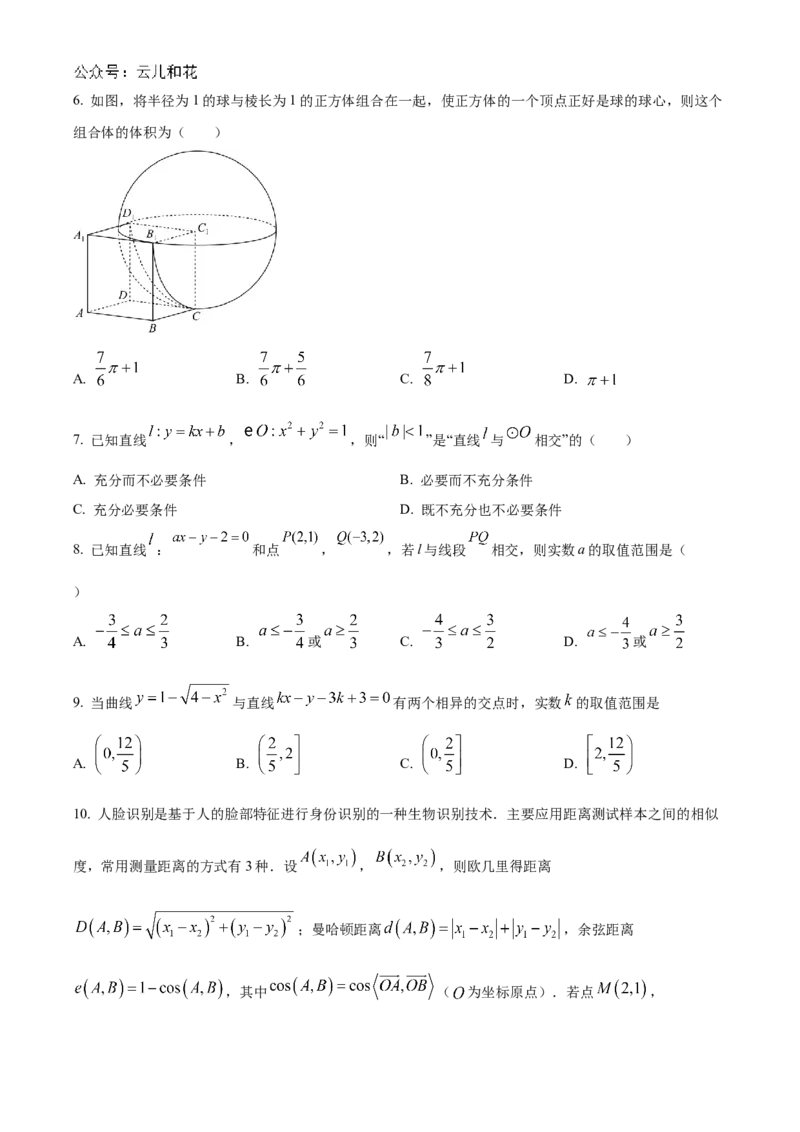
D 若 ,则6. 如图,将半径为1的球与棱长为1的正方体组合在一起,使正方体的一个顶点正好是球的球心,则这个
组合体的体积为( )
A. B. C. D.
7. 已知直线 , ,则“ ”是“直线 与 相交”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 已知直线 : 和点 , ,若l与线段 相交,则实数a的取值范围是(
)
A. B. 或 C. D. 或
9. 当曲线 与直线 有两个相异的交点时,实数 的取值范围是
A. B. C. D.
10. 人脸识别是基于人的脸部特征进行身份识别的一种生物识别技术.主要应用距离测试样本之间的相似
度,常用测量距离的方式有3种.设 , ,则欧几里得距离
;曼哈顿距离 ,余弦距离
,其中 ( 为坐标原点).若点 ,,则 的最大值为( )
A. B. C. D.
二、填空题,共5小题,每小题4分,共20分.
11. 两平行直线 : 与 : 之间的距离是_____.
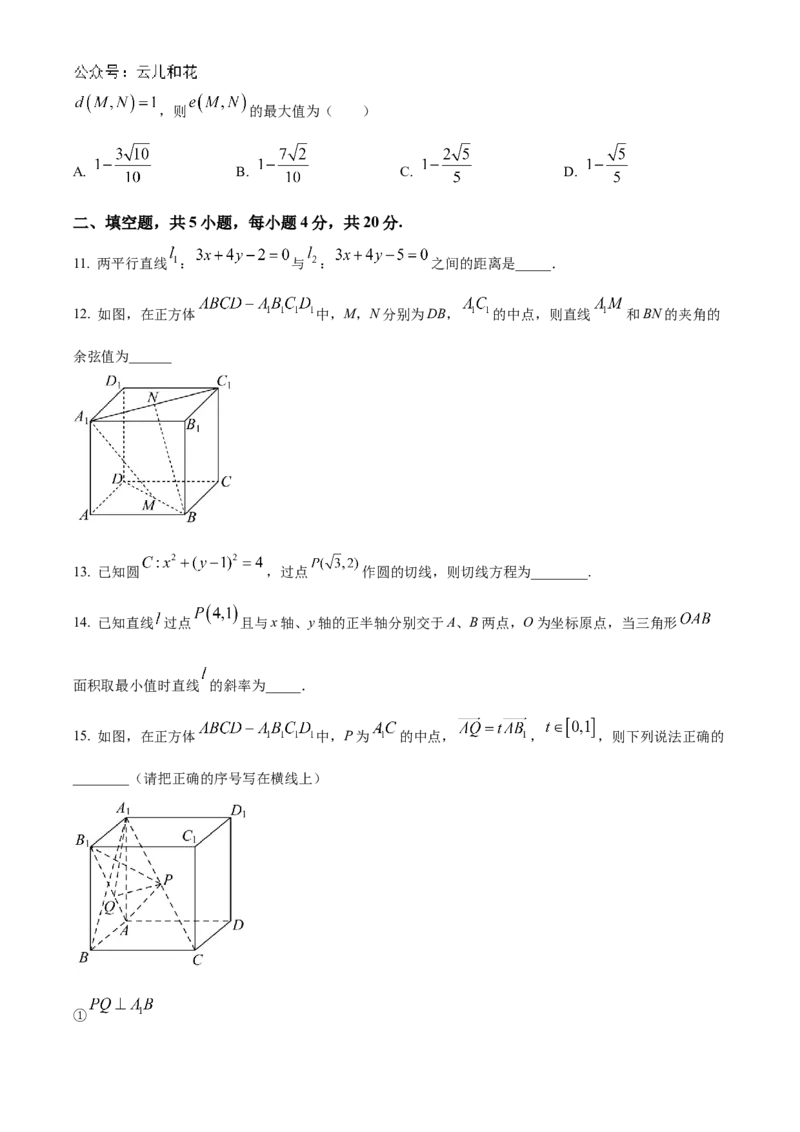
12. 如图,在正方体 中,M,N分别为DB, 的中点,则直线 和BN的夹角的
余弦值为______
13. 已知圆 ,过点 作圆的切线,则切线方程为________.
14. 已知直线 过点 且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点,当三角形
面积取最小值时直线 的斜率为_____.
15. 如图,在正方体 中,P为 的中点, , ,则下列说法正确的
________(请把正确的序号写在横线上)
①②当 时, 平面
③当 时,PQ与CD所成角的余弦值为
④当 时, 平面
三、解答题,共4小题,每小题10分,共40分.解答应写出文字说明,演算步骤或证明过程.
16. 已知 的顶点 , , .
(1)求边 上的高 所在直线的方程;
(2)求边 上的中线 所在直线的方程;
(3)求 的面积.
的
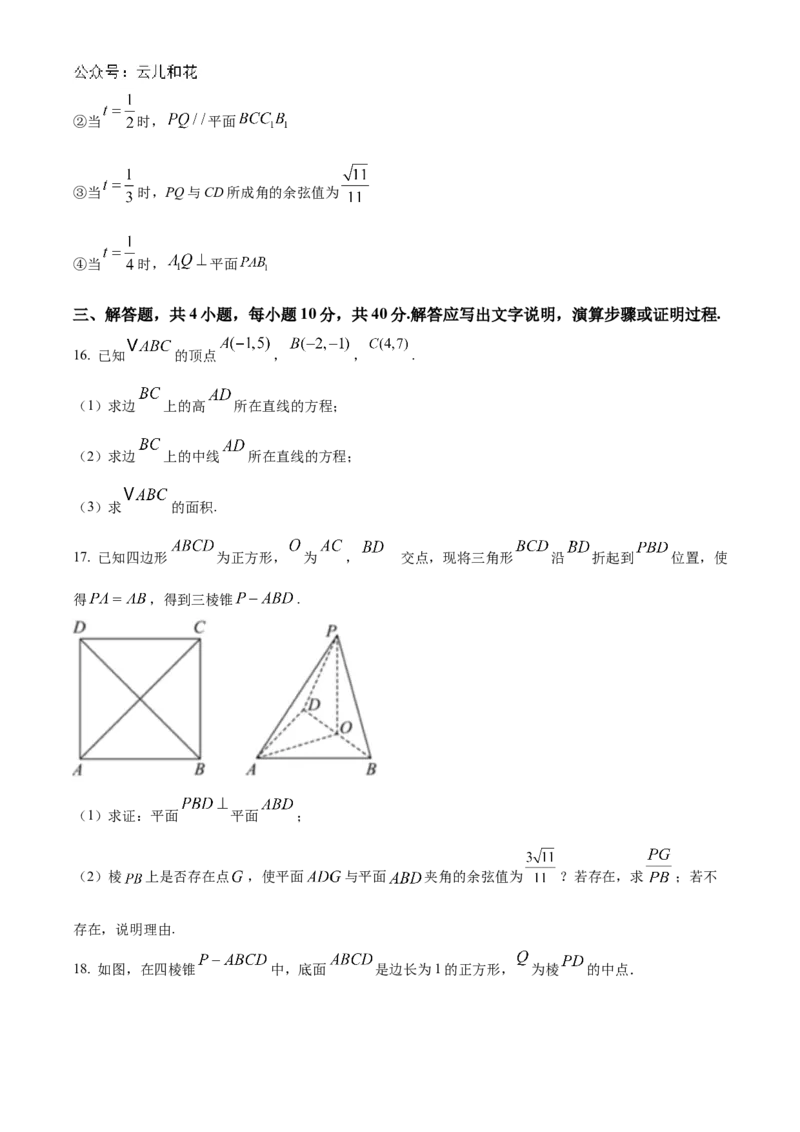
17. 已知四边形 为正方形, 为 , 交点,现将三角形 沿 折起到 位置,使
得 ,得到三棱锥 .
(1)求证:平面 平面 ;
(2)棱 上是否存在点 ,使平面 与平面 夹角的余弦值为 ?若存在,求 ;若不
存在,说明理由.
18. 如图,在四棱锥 中,底面 是边长为1的正方形, 为棱 的中点.(1)求证: 平面 ;
(2)若 ,再从条件①、条件②、条件③中选择若干个作为已知,使四棱锥 唯一确定,
并求:
(i)直线 与平面 所成角的正弦值;
(ii)点 到平面 的距离.
条件①:二面角 的大小为 ;
条件②:
条件③: .
19. 设二次函数 的图象与两坐标轴的交点分别记为 , , ,曲线 是经过这三点的圆.
(1)求圆 的方程;
(2)过 作直线 与圆 相交于 , 两点.
(i) 是否是定值?如果是,请求出这个定值;
(ii)设 ,求 的最大值.