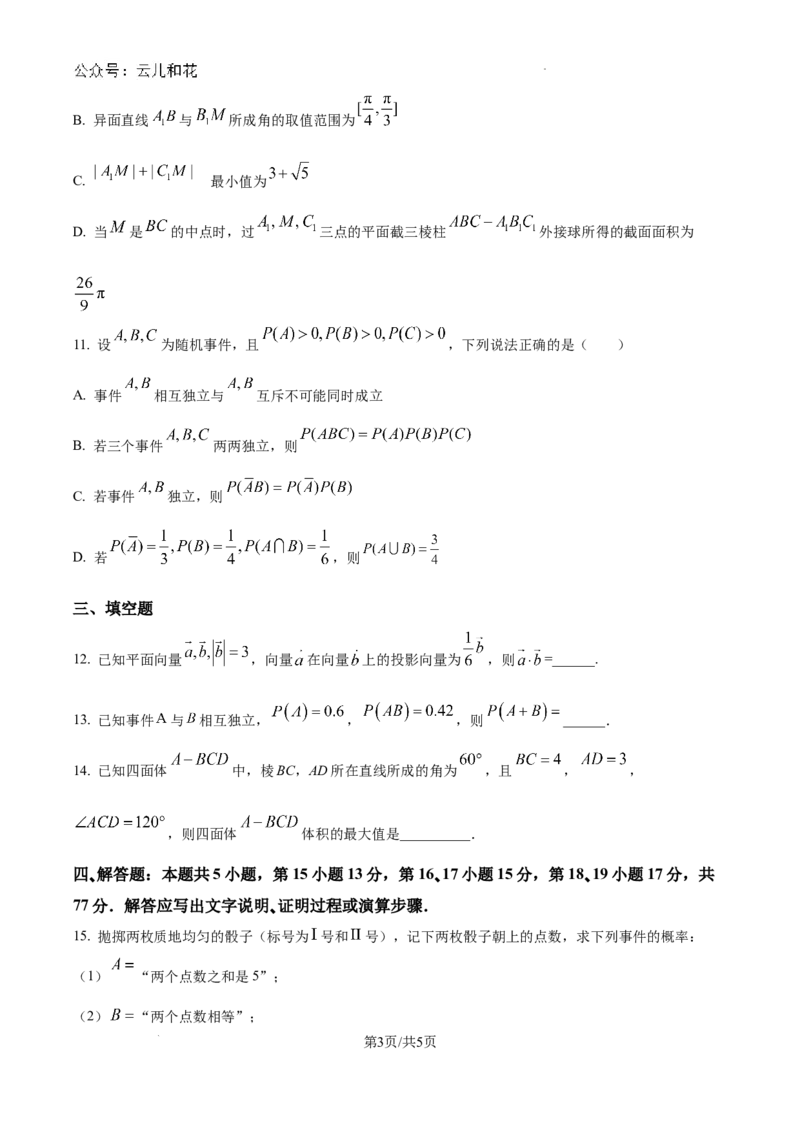文档内容
高二开学考数学
一、单选题(每小题5分,共40分)
1. 样本数据24,13,14,18,12,14,20,16的75%分位数为( )
A. 17 B. 18 C. 19 D. 20
2. 设事件A,B,已知P(A)= ,P(B)= ,P(A∪B)= ,则A,B之间的关系一定为( )
A. 两个任意事件 B. 互斥事件
C. 非互斥事件 D. 对立事件
3. 某圆台上底面圆半径为1,下底面圆半径为2,母线长为 ,则该圆台的体积为( )
.
A B. C. D.
4. 已知向量 , 满足 , ,且 , 的夹角为 ,则向量 在向量 方向上的投影向量为
( )
A. B. C. D.
5. 已知非零向量 满足 ,且向量 在向量 上的投影向量为 ,则 与 的夹角为( )
A. B. C. D.
6. 在 中,内角 的对边分别为 ,且 ,则 的最大值
是( )
.
A B. C. D.
7. 已知函数 ,若对任意 实数 , 在区间 上的值域
的
第1页/共5页
学科网(北京)股份有限公司均为 ,则 的取值范围为( )
A. B. C. D.
8. 某高校的入学面试中有3道难度相当的题目,李华答对每道题目的概率都是 ,若每位面试者共有三次
机会,一旦某次答对抽到的题目,则面试通过,否则就一直抽题到第3次为止,假设对抽到的不同题目能
否答对是独立的,则李华最终通过面试的概率为( )
A. B. C. D.
二、多选题(本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合题
目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. 已知平面向量 , ,则( )
A. 当 时, B. 若 ,则
的
C. 若 ,则 D. 若 与 夹角为钝角,则
10. 在直三棱柱 中, ,且 , 为线段 上的动点,则
下列结论中正确的是( )
A.
第2页/共5页
学科网(北京)股份有限公司B. 异面直线 与 所成角的取值范围为
的
C. 最小值为
D. 当 是 的中点时,过 三点的平面截三棱柱 外接球所得的截面面积为
11. 设 为随机事件,且 ,下列说法正确的是( )
A. 事件 相互独立与 互斥不可能同时成立
B. 若三个事件 两两独立,则
C. 若事件 独立,则
D. 若 ,则
三、填空题
12. 已知平面向量 ,向量 在向量 上的投影向量为 ,则 =______.
13. 已知事件 与 相互独立, , ,则 ______.
14. 已知四面体 中,棱BC,AD所在直线所成的角为 ,且 , ,
,则四面体 体积的最大值是__________.
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共
77分.解答应写出文字说明、证明过程或演算步骤.
15. 抛掷两枚质地均匀的骰子(标号为 号和 号),记下两枚骰子朝上的点数,求下列事件的概率:
(1) “两个点数之和是5”;
(2) “两个点数相等”;
第3页/共5页
学科网(北京)股份有限公司(3) “ 号骰子的点数大于 号骰子的点数”.
16. 已知平面向量 , , ,且 , .
(1)求 和 ;
(2)若 , ,求向量 和向量 的夹角的大小.
17. 在 中,内角A,B,C的对边分别为 ,且 .
(1)求角 ;
(2)若 ,求 面积的最大值.
18. 2024年4月25日,神舟十八号载人飞船顺利发射,本次乘组将首次在空间站实施水生生态项目,即要
实现“太空养鱼”,意味着我们有能力在太空构造新的生态环境和生态系统.郑州航天电子技术有限公司为
此次任各提供了科技产品和技术服务,该公司为了提高单位职工的工作热情,开展了知识比赛,满分120
分,100分及以上为“航天达人”,结果航天达人有t人,这t人按年龄分成了5组,其中第一组: ,
第二组: ,第三组: ,第四组, ,第五组: ,得到的频率分布直方图如
下图,已知第一组有10个人.
(1)根据频率分布直方图,估计这t人年龄的第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任“航天工程”的宣传大使.若第四组宣传大使
的年龄的平均数与方差分别为36和 ,第五组宣传大使的年龄的平均数与方差分别为42和1,据此估计
第4页/共5页
学科网(北京)股份有限公司这t人中35~45岁所有人的年龄的平均数和方差.(分层随机抽样中各层抽取的样本量、样本平均数和样
本方差分别为:m, , ,n, , .记总体的样本平均数为 ,样本方差为 ,则
,
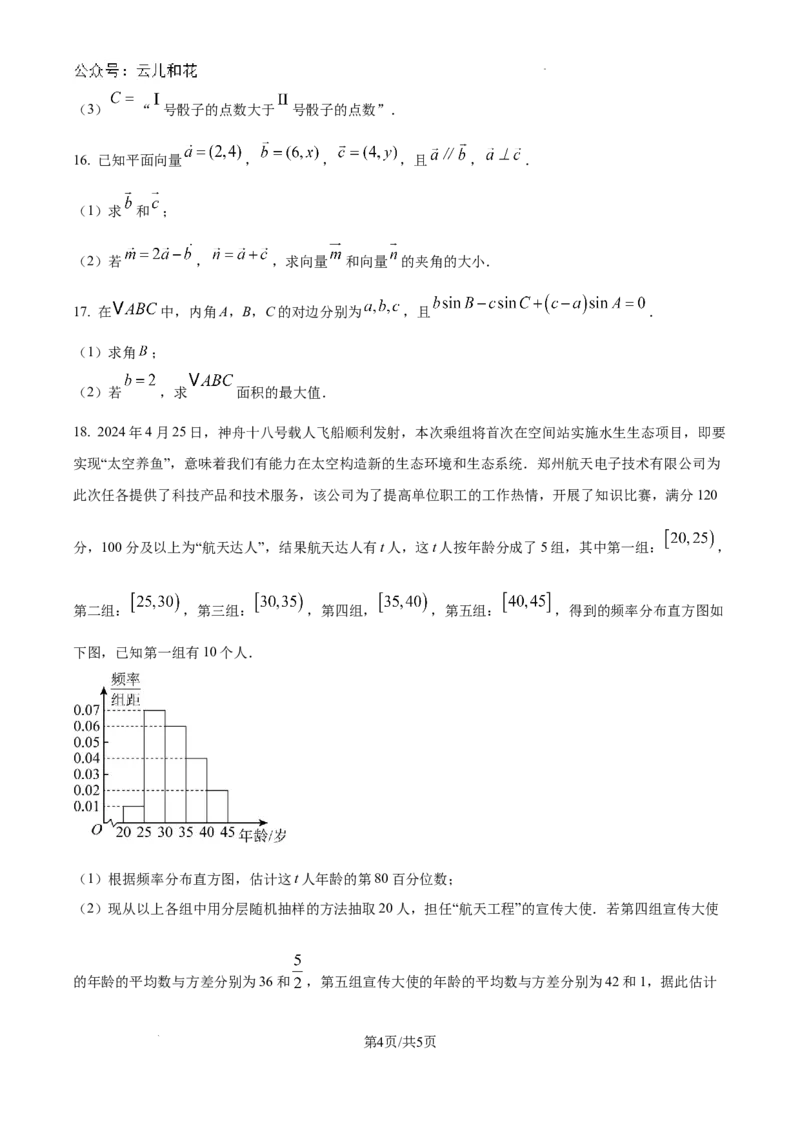
19. 如图是函数 图象的一部分.
(1)求函数 的解析式;
(2)求函数 的单调区间;
(3)记方程 在 上的根从小到大依次为 ,若
,试求 与 的值.
第5页/共5页
学科网(北京)股份有限公司