文档内容
2023 级普通高中学科素养水平监测试卷
数学
2024.11
注意事项:
1.答卷前,考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需要改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本
试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 直线 的倾斜角为( )
A. B. C. D.
2. 椭圆 的离心率为( )
A. B. C. D.
3. 已知 是直线 的方向向量, 为平面 的法向量,若 ,则 ( )
A. B. C. D.
.
4 若圆 与圆 有3条公切线,则 ( )
A. 5 B. 4 C. 3 D. 2
5. 空间三点 , , ,则以 , 为邻边的平行四边形的面积为( )
A. B. C. 7 D.6. 若圆 ,点 在直线 上,过点 作圆 的切线,切点为 ,则切线长
的最小值为( )
A. 1 B. 2 C. D. 4
7. 若 , 两点到直线 的距离相等,则 ( )
.
A B. C. 2或 D. 2或
8. 设 为坐标原点, , 为椭圆 的两个焦点,点 在 上, ,则
( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 若直线过点 ,且在两坐标轴上截距相等,则直线 方程可能为( )
A. B.
C. D.
10. 在平面直角坐标系 中,已知 , ,点 满足 ,设点 的轨
迹为 ,则( )
A. 当 时, 的方程是
B. 当 时,以 为直径的圆与 的公共弦长为
C. 当 时,圆 的圆心在线段 的延长线上的
D. 以 为直径 圆始终与 相交
11. 如图是数学家Germinal Dandelin用来证明一个平面截圆锥侧面得到的截口曲线是椭圆的模型(称为
“Dandelin双球”).在圆锥内放两个大小不同的小球,使得它们分别与圆锥的侧面、截面相切,截面分别与
球 ,球 切于点 , ( , 是截口椭圆 的焦点).设图中球 ,球 的半径分别为3和1,球
心距 ,则( )
A. 椭圆 的中心在直线 上
B.
C. 直线 与椭圆 所在平面所成的角为
D. 椭圆 的离心率为
三、填空题:本题共3小题,每小题5分,共15分.
12. 若点 是点 在坐标平面 内的射影,则 ________.
13. 若圆 上恰有 个点到直线 的距离等于 ,则 的取值范围是________.
的
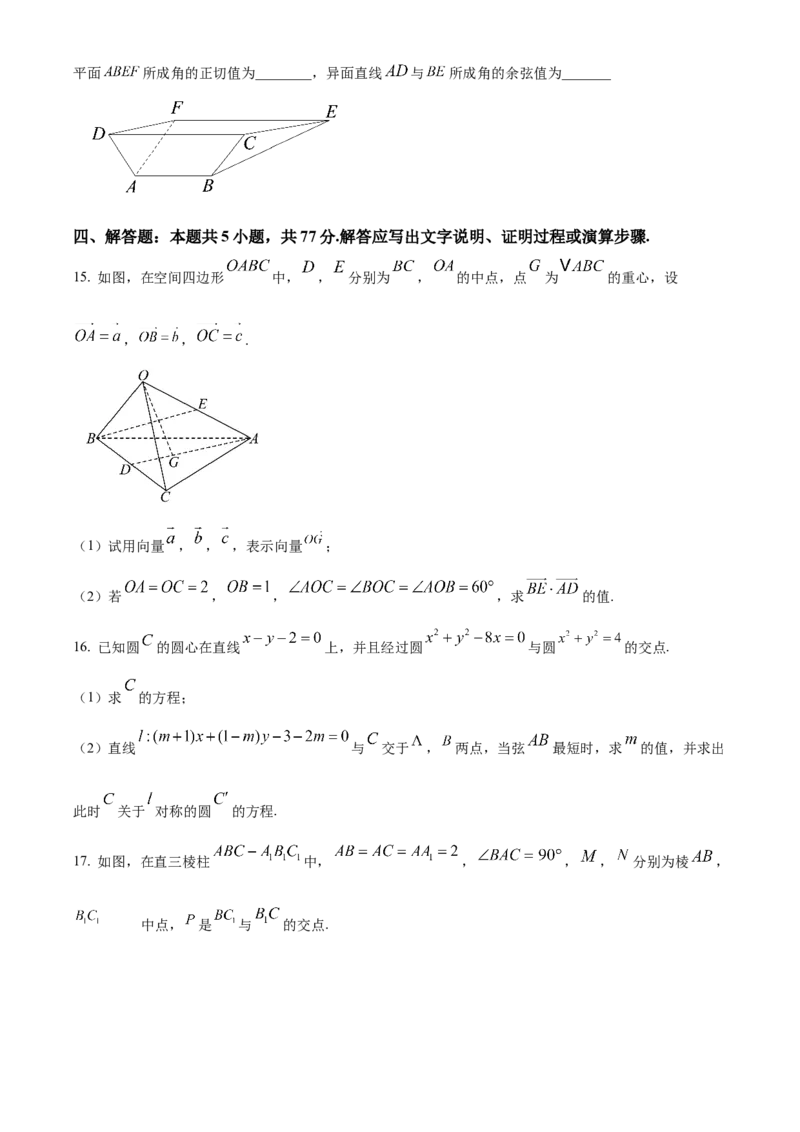
14. 《九章算术》中记录 “羡除”是算学和建筑学术语,指的是一段类似地下车库入口形状的几何体.
如图,羡除 中,四边形 , 均为等腰梯形, , , 互相平行,平面
平面 ,梯形 , 的高分别为2,4,且 , , ,则 与平面 所成角的正切值为________,异面直线 与 所成角的余弦值为_______
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 如图,在空间四边形 中, , 分别为 , 的中点,点 为 的重心,设
, , .
(1)试用向量 , , ,表示向量 ;
(2)若 , , ,求 的值.
16. 已知圆 的圆心在直线 上,并且经过圆 与圆 的交点.
(1)求 的方程;
(2)直线 与 交于 , 两点,当弦 最短时,求 的值,并求出
此时 关于 对称的圆 的方程.
17. 如图,在直三棱柱 中, , , , 分别为棱 ,
的
中点, 是 与 的交点.(1)求点 到平面 的距离;
(2)在线段 上是否存在一点 ,使 平面 ,若存在,求出 的值,若不存在,请说明
理由.
18. 在圆 上任取一点 ,过 作 轴的垂线段 ,垂足为 ,点 在线段 的延长线
上,且 ,当 在圆 上运动时,点 形成的轨迹为 .(当 经过圆 与 轴的交点时,规定
点 与点 重合.)
(1)求 的方程;
(2)设 的上顶点为 ,过点 作斜率为 的直线与椭圆 交于不同的两点 , ,直线 ,
分别与 轴交于点 , ,证明:线段 的中点为定点.
19. 已知曲线 ,对坐标平面上任意一点 ,定义 ,若两点 , ,满
足 ,称点 , 在曲线 的同侧; ,称点 , 在曲线 的两侧.
(1)若曲线 ,判断 , 两点在曲线 的同侧还是两侧;
(2)已知曲线 , 为坐标原点,求点集 所
构成图形的面积;(3)记到点 与到 轴的距离之和为 的点的轨迹为曲线 ,曲线 ,
若曲线 上总存在两点 , 在曲线 两侧,求曲线 的方程和实数 的取值范围.