攀枝花市2024届高三第一次统一考试文数答案(1)_2023年11月_0211月合集_2024届四川省攀枝花市高三第一次统一考试_四川省攀枝花市2024届高三第一次统一考试文科数学

攀枝花市 2024 届高三第一次统考数学（文科） 参考答案 一、选择题：（每小题5分，共60分） （1~5）BACCB （6~10）DACDA （11~12）CD 二、填空题：（每小题5分，共20分） 25 5−1 13、 1 14、 2 15、 16、 (0， ] 2 2 三、解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.） 17、（本小题满分12分） 解：（1）因为2S =na ，所以当n≥2时，2S =(n−1)a .……………………1分 n n+1 n−1 n 两式相减得：(n+1)a =na .……………………3分 n n+1 a a a 从而 n = n+1 ，即数列{ n}是常数列.……………………5分 n n+1 n a a 又 1 =1，所以 n =1⇒a =n(n∈N*).……………………6分 1 n n （2）因为a ⋅2n =n⋅2n，所以T =1×21+2×22 +3×23++n×2n， n n 2T = 1×22 +2×23 ++(n−1)×2n +n×2n+1.………………8分 n 两式相减得：−T = 21+22 +23 ++2n −n×2n+1 n 2×(1−2n) = −n×2n+1.……………………10分 1−2 =(1−n)2n+1−2 即T =2−( 1−n ) 2n+1(n∈N*).……………………12分 n 18、（本小题满分12分） 解：（1）由题意有bcosC+ 3bsinC−a−c=0， 由正弦定理得sinBcosC+ 3sinBsinC−sinA−sinC =0.……………………2分 ∵A+B+C =π， ∴sinBcosC+ 3sinBsinC−sin ( B+C )−sinC =0， ∴ 3sinBsinC−cosBsinC−sinC =0 π 1 ∵C∈( 0,π)， ∴sinC ≠0，所以sin(B− )= .……………………4分 6 2 π π π ∵B∈( 0,π)，∴B− = ，故B = .……………………5分 6 6 3 b ∴外接圆直径2R= =2，故R=1.……………………6分 sinB π   （2）由题意知B = ，而BA⋅BC =accosB =6，所以ac=12.……………………7分 3 由余弦定理知b2 =a2 +c2 −2accosB=(a+c)2 −2ac(1+cosB)=12，所以b=2 3.………………9分 高三第一次统考数学（文）参答 第 1 页 共 4 页 {#{QQABCYQQogigABJAAQgCQw3iCkAQkBECACoGABAIsAABgANABAA=}#}1 又∵S = ac⋅sinB=3 3.…………………10分 ∆ABC 2 1 由△ABC的面积S = ( a+b+c ) r =3 3，得r =1.…………………12分 ∆ABC 2 19、（本小题满分12分） 证明：（1）分别取PB，PC的中点F，G，连接EF，DG，FG.……………………2分 ∵四边形ABCD，E是AD的中点， 1 1 ∴DE = BC，DE//BC，FG = BC，FG//BC ， 2 2 ∴DE = FG，DE//FG G ∴四边形DEFG是平行四边形.……………………4分 ∴EF//DG，又EF ⊄平面PCD，DG⊂平面PCD， F ∴EF//平面PCD.……………………6分 （2）易知∆CDE、∆PDE为直角三角形， 1 1 1 1 则S = CD⋅DE = ×2 2×1= 2 ，S = PA⋅DE = ×2×1=1.……………………8分 ∆CDE 2 2 ∆PDE 2 2 3 又∵PD= PC =CD=2 2 ∴S = PD2 =2 3.……………………9分 ∆PCD 4 P （法一）∵PE = 5,PC =2 2,CE =3 过点P作PH ⊥CE，垂足为H ，设HE = x，CH =3−x 则PH2 = PC2 −CH2 = PE2 −HE2，即PH2 =8−(3−x)2 =5−x2 解得x=1，从而PH =2 C H E 1 1 ∴S = CE⋅PH = ×3×2=3.……………………11分 ∆PCE 2 2 PC2 +CE2 −PE2 12 2 （法二）∵PE = 5,PC =2 2,CE =3 ∴由余弦定理得cos∠PCE = = = 2PC⋅CE 12 2 2 2 1 1 2 从而sin∠PCE = ，∴S = PC⋅CE⋅sin∠PCE = ×2 2×3× =3.……………………11分 2 ∆PCE 2 2 2 ∴S =S +S +S +S =1+ 2+2 3+3=4+ 2+2 3.……………………12分 P−CDE表面积 ∆PDE ∆CDE ∆PCD ∆PCE 20、（本小题满分12分） 解：（1）由题知：c= 2得到a2−b2 =2.……………………1分 b2 6 b2 1 又e= 1− = ⇒ = .……………………2分 a2 3 a2 3 x2 解得a2 =3，b2 =1，则椭圆C的方程为 + y2 =1.……………………4分 3 2 （2）由已知直线l的斜率存在且不为0，设直线l: y =kx−2，则P( ,0).……………………5分 k y+ y x−x 设A(x ,y ),B(x ,y )，则D(x ,−y )，直线BD的方程： 1 = 1 .……………………7分 1 1 2 2 1 1 y + y x −x 2 1 2 1 x y +x y 2kx x −2(x +x ) 令y =0，得点Q的横坐标为x = 1 2 2 1 = 1 2 1 2 ① Q y + y k(x +x )−4 1 2 1 2 高三第一次统考数学（文）参答 第 2 页 共 4 页 {#{QQABCYQQogigABJAAQgCQw3iCkAQkBECACoGABAIsAABgANABAA=}#}y =kx−2  由x2 得(3k2 +1)x2 −12kx+9=0，则∆>0⇒k2 >1  + y2 =1  3 12k 9 且x +x = , x x = .……………………9分 1 2 3k2 +1 1 2 3k2 +1 18k−2⋅12k −6k 3k 代入①，则x = = = .……………………10分 Q 12k2 −4(3k2 +1) −4 2 2 3k 2 3k 2 3 从而 OP + OQ =|x |+|x |=| |+| |≥2 3，当且仅当| |=| |，即k =± 时取到等号. P Q k 2 k 2 3 所以 OP + OQ 的取值范围为[2 3,+∞).……………………12分 21、（本小题满分12分） 解：（1）a=1时，函数 f(x)=ex −x的定义域为R， f′(x)=ex −1.……………………1分 由 f′(x)=0解得x=0.……………………2分 当x∈(−∞,0 ) 时， f′(x)<0， f ( x ) 在x∈(−∞,0 ) 单调递减； 当x∈( 0,+∞) 时， f′(x)>0， f ( x ) 在x∈( 0,+∞) 单调递增.……………………3分 （2）g(x)=(x2 −a−1)ex，则g′(x)=(x2 +2x−a−1)ex．…………………4分 根据题意，得方程x2 +2x−a−1=0有两个不同的实根x ,x (x < x )， 1 2 1 2 ∴∆>0，即a >−2且x +x =−2，所以x <−1< x ．…………………5分 1 2 1 2 由tg(x )≥(2+x )(ex 2 +x 2 −3)，可得t(x 2 −a−1)ex 2 ≥(2+x )(ex 2 +x 2 −3) 2 1 2 2 1 2 又x 2 −a−1=−2x ,2+x =−x 2 2 1 2 ∴总有−2tx ex 2 ≥(−x )(ex 2 +x 2 −3)⇒ x [2tex 2 −(ex 2 +x 2 −3)]≤0对x >−1恒成立．…………………6分 2 2 2 2 2 2 ①当x =0时，x [2tex 2 −(ex 2 +x 2 −3)]≤0恒成立，此时t∈R；………………7分 2 2 2 ex 2 +x 2 −3 ②当x (1,0)时，2tex 2 −(ex 2 +x 2 −3)≥0成立，即2t ≥ 2 2 2 ex 2 ex 2 x 23 x 22x 3 (x 1)(x 3) 令函数h(x ) 2 ，则h(x ) 2 2  2 2 0在x (1,0)恒成立 2 ex 2 2 ex 2 ex 2 2 故h(x )在x (1,0)单调递增，所以2th(0)2t1．………………9分 2 2 ex 2 +x 2 −3 ③当x (0,)时，2tex 2 −(ex 2 +x 2 −3)≤0成立，即2t ≤ 2 2 2 ex 2 ex 2 x 23 (x 1)(x 3) 由函数h(x ) 2 ，则h(x ) 2 2 0，解得x 3 2 ex 2 2 ex 2 2 当x (0,3)时，h(x )0，h(x )单调递增；当x (3,)时，h(x )0，h(x )单调递减 2 2 2 2 2 2 x 23 又h(x )1 2 ，当x 时，h(x )1 2 ex 2 2 2 ∴所以2th(0)2t1．…………………11分 综上所述，t =−1．……………………12分 请考生在22~23两题中任选一题作答，如果多做，则按所做的第一题记分．作答时用2B铅笔在答题卡上 把所选题目对应题号右侧的方框涂黑． 高三第一次统考数学（文）参答 第 3 页 共 4 页 {#{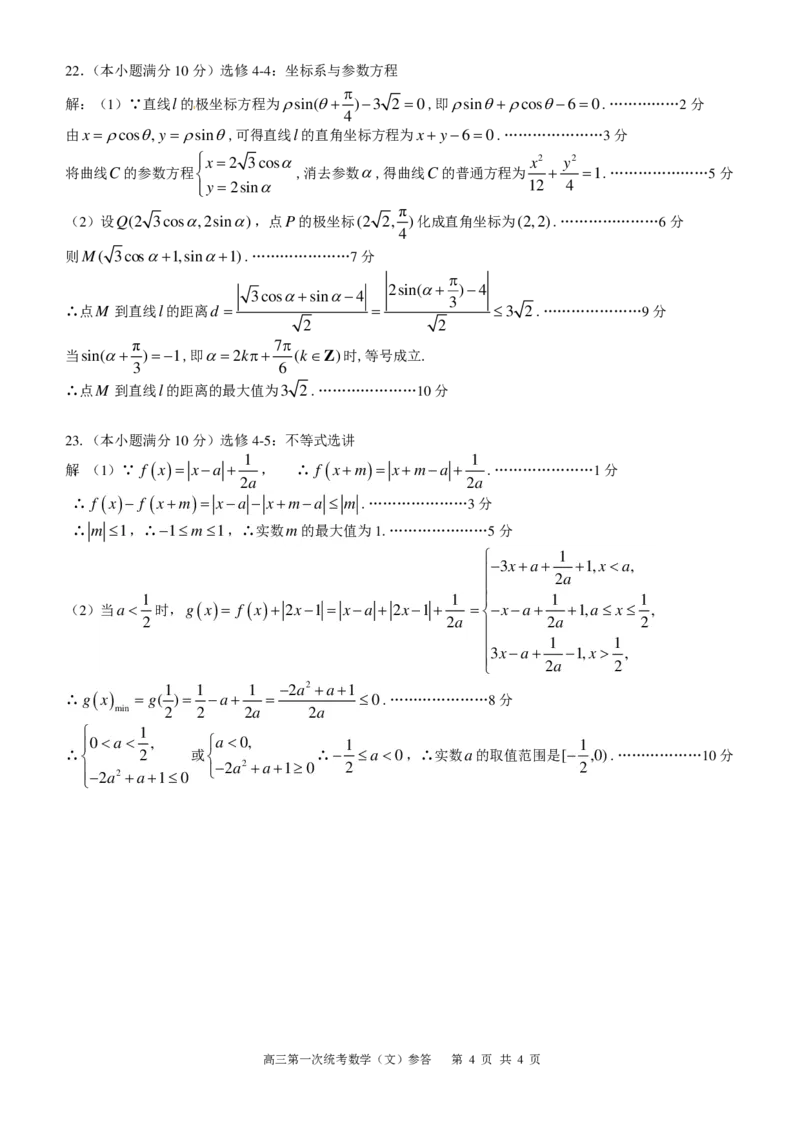QQABCYQQogigABJAAQgCQw3iCkAQkBECACoGABAIsAABgANABAA=}#}22．（本小题满分10分）选修4-4：坐标系与参数方程 π 解：（1）∵直线l的极坐标方程为ρsin(θ+ )−3 2 =0,即ρsinθ+ρcosθ−6=0.……………2分 4 由x=ρcosθ,y =ρsinθ,可得直线l的直角坐标方程为x+ y−6=0.…………………3分 x=2 3cosα x2 y2 将曲线C的参数方程 ,消去参数α,得曲线C的普通方程为 + =1.…………………5分 y =2sinα 12 4 π （2）设Q(2 3cosα,2sinα)，点P的极坐标(2 2, )化成直角坐标为(2,2).…………………6分 4 则M( 3cosα+1,sinα+1).…………………7分 π 2sin(α+ )−4 3cosα+sinα−4 3 ∴点M 到直线l的距离d = = ≤3 2.…………………9分 2 2 π 7π 当sin(α+ )=−1,即α=2kπ+ (k∈Z)时,等号成立. 3 6 ∴点M 到直线l的距离的最大值为3 2.…………………10分 23.（本小题满分10分）选修4-5：不等式选讲 1 1 解：（1）∵ f ( x )= x−a + ， ∴ f ( x+m )= x+m−a + .…………………1分 2a 2a ∴ f ( x )− f ( x+m )= x−a − x+m−a ≤ m .…………………3分 ∴ m ≤1，∴−1≤m≤1，∴实数m的最大值为1.…………………5分  1 −3x+a+ +1,x ,   2a 2 1 1 1 −2a2 +a+1 ∴g ( x ) = g( )= −a+ = ≤0.…………………8分 min 2 2 2a 2a  1 0