江苏省扬州市2024-2025学年高二上学期1月期末检测数学试题_2024-2025高二（7-7月题库）_2025年02月试卷_0207江苏省扬州市2024-2025学年高二上学期1月期末考试

2024－2025 学年第一学期期末检测
高 二 数 学
2025.1
注意事项：
1. 答题前，考生务必在答题卡上将自己的学校、姓名、准考证号用0.5毫米黑色签字
笔填写清楚，考生考试条形码由监考老师粘贴在答题卡上的“条形码粘贴处”.
2. 选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上，如需改动，用橡皮擦
擦干净后再填涂其它答案；非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答，超
出答题区域答题的答案无效；在草稿纸上、试卷上答题无效.
一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中， 只
有一项是符合题目要求的．
1． 已知直线
第 1 页 (共 4 页)
l 经过 (1 , 2 ) 和 ( 2 ,1 ) 两点，则 l 的倾斜角为（ ）

A． B．
4


4
C．

4
D．
 
4
2． 双曲线 2 x 2  y 2  1 的渐近线方程为（ ）
A．y 2x B． y  
2
2
x C． y   2 x D． y  
1
2
x
3． 设等差数列  a
n
 的前 n 项和为 S
n
，已知 a
1
 a
9
 1 0 ， a
5
a
6
 3 5 ，则S （ ）
10
A．50 B．60 C．70 D．80
4. 设 m , n 为实数，若直线mxny20与圆 x 2  y 2  4 相切，则点P(m,n)与圆的位置
关系是（ ）
A．在圆上 B．在圆外 C．在圆内 D．不能确定
x2 y2
5． 设椭圆  1(ab0)的半焦距为c，直线
a2 b2
l 过F(c,0)，B(0,b)两点，坐标原点
1
到直线l的距离等于 FB，则椭圆的离心率为（ ）
2
2 3
A．1 B． C． D． 21
2 3
{#{QQABAYYAogCoQBAAARgCUwHACgKQkhEACQgGwAAMIAAASBNABCA=}#}6． 过抛物线
第 2 页 (共 4 页)
y 2  4 x 的焦点 F 作斜率为 1 的弦AB，点 A 在第一象限，则
A
F
F
B
 （ ）
A． 2 B． 2  1 C．2 2 D. 3  2 2
7． 已知直线 l : x  a y  a  1  0 ， a  R 与圆 C : ( x  2 ) 2  y 2  4 交于 A , B 两点，则 A B 长
的最小值为（ ）
A． 2 B．2 C． 2 2 D． 4
8． 已知 m , n , p , q 均为实数，则 ( m  p ) 2  ( n  p  1 ) 2  ( m  q ) 2  ( n  q  3 ) 2 的最小
值为（ ）
A． 1 B． 2 C． 3 D．2
二、选择题：本大题共3小题，每小题6分，共18分．在每小题给出的选项中， 有多项
符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．
9． 已知直线 l1 : a x  y  1  0 ， l2 : x  a 2 y  1  0 ，下列选项正确的有（ ）
A．若 a  0 ，则l 斜率不存在 B．若
1
l1 不经过第三象限，则 a  0
C．若 l1  l2 ，则 a  0 或  1 D．若 a  1 ，则l l
1 2
10．已知圆O :(x3)2 (y4)2 16与圆
1
O
2
: x 2  y 2  r 2 ( r  0 ) ，下列选项正确的有（ ）
A．若r1，则两圆外切
B．若r1，则直线 x = 1  为两圆的一条公切线
C．若 r  3 ，则两圆公共弦所在直线的方程为3x4y90
24
D．若r3，则两圆公共弦的长度为
5
11．平面直角坐标系xOy中，A(1,0)，B(1,0)，动点 P 满足 PA  PB 1，记点 P 的轨迹
为曲线C，在第一象限内任取曲线C上点 Q ( x
0
, y
0
) ，记直线OQ的倾斜角为，斜率
为k，下列选项正确的有（ ）
A．曲线C经过点( 2,0) B．曲线C是中心对称图形
OQ2
C．k的最大值为1 D． 为定值
cos2
{#{QQABAYYAogCoQBAAARgCUwHACgKQkhEACQgGwAAMIAAASBNABCA=}#}三、填空题：本大题共3小题，每小题5分，共15分.
12．点
第 3 页 (共 4 页)
A ( 0 , 2 ) 关于直线 l : x  y  1  0 的对称点坐标为 ▲ ．
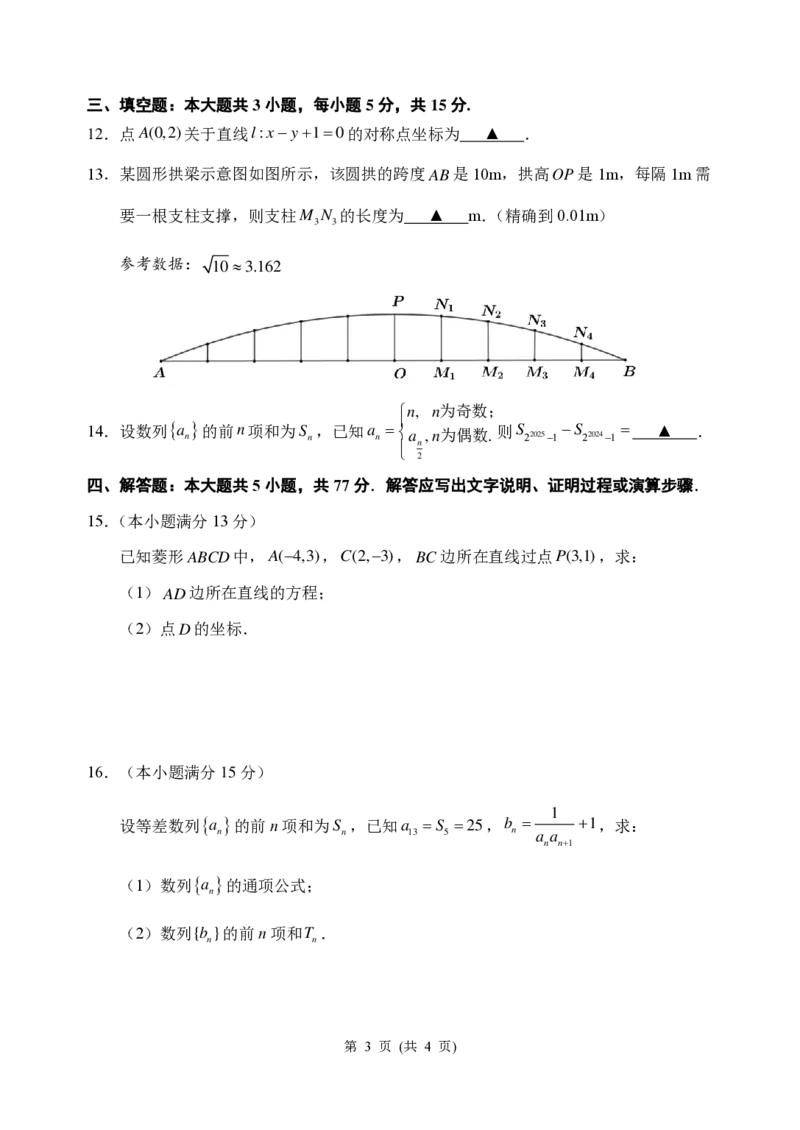
13．某圆形拱梁示意图如图所示，该圆拱的跨度 A B 是10m，拱高 O P 是1m，每隔1m需
要一根支柱支撑，则支柱M N 的长度为 ▲ m．（精确到0.01m）
3 3
参考数据： 1 0  3 .1 6 2
14．设数列  a n  的前 n 项和为 S n ，已知 a n 
 n
a
,
n2
,
n
n
为
为
奇
偶
数
数
；
. 则 S 2 2025  1  S 2 2024  1  ▲ ．
四、解答题：本大题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15．（本小题满分13分）
已知菱形 A B C D 中， A (  4 , 3 ) ， C ( 2 ,  3 ) ， B C 边所在直线过点 P ( 3 ,1 ) ，求：
（1） A D 边所在直线的方程；
（2）点 D 的坐标．
16．（本小题满分15分）
设等差数列  a
n
 的前n项和为 S
n
，已知a S 25，
13 5
b
n

a
n
1
a
n  1
 1 ，求：
（1）数列  a
n
 的通项公式；
（2）数列{b }的前n项和T ．
n n
{#{QQABAYYAogCoQBAAARgCUwHACgKQkhEACQgGwAAMIAAASBNABCA=}#}17．（本小题满分15分）
已知圆心在直线
第 4 页 (共 4 页)
y  x 上的圆C经过点 A ( 3 ,1 ) ，且与直线 x  y  2 2  0 相切．
（1）求圆C的标准方程；
（2）设 P 为直线 m : x  2 y  4  0 上的点，满足：过点 P 引圆 C 的切线，切点分别为
M和 N ，MPN 60，试求所有满足条件的点 P 的坐标．
18．（本小题满分17分）
已知椭圆 E :
x
a
2
2

y
b
2
2
 1 ( a  b  0 ) 经过点 M (
4
3
, 
1
3
) ，且右焦点为F(1,0)．
（1）求椭圆 E 的标准方程；
（2）已知直线 l 过椭圆 E 的上顶点 P ，过椭圆 E 的右顶点 A 作 A B  l ，垂足为 B ，
作 A C l 交椭圆E于点 C ，当 △ A B C 面积最大时，求直线l的方程．
19．（本小题满分17分）
已知有穷数列  a
n
 满足 0  a
1
 a
2
  a
n
且 n  3 ，
集合A 

a a |1i jn,i,
jN*
, 记
n i j
A
n
中元素个数为|A |．
n
（1）若数列  a
n
 满足a n，求
n
| A
4
| 和 | A
n
| 的值；
（2）若数列a 满足
n
a
n
 2 n ，求 A
n
中所有元素之和；
（3）若数列  a
n
 满足2a a a ，
2 1 3
| A
n
| 2 n  3 ，则数列  a
n
 是等差数列吗？如果是，
请说明理由；如果不是，请举反例．
{#{QQABAYYAogCoQBAAARgCUwHACgKQkhEACQgGwAAMIAAASBNABCA=}#}