文档内容
高三数学考试卷参考答案
!!#!因为""#$!%"!"&"’#"所以#$""#%$!(")#!
$
(+",
&!*!%$ $$&+’,%$!-,%$)+,"则%$$)-,!
!+,
& 槡’&-&&
’!#!由题可知 $&槡&"即&$&槡&’"则(的离心率)$ $’!
’ ’
!
(!.!因为/,0!12/"$12/!/,0"-!"所以/,0!12/"+12/!/,0"$/,0$!+" %$!"则!+"$ -
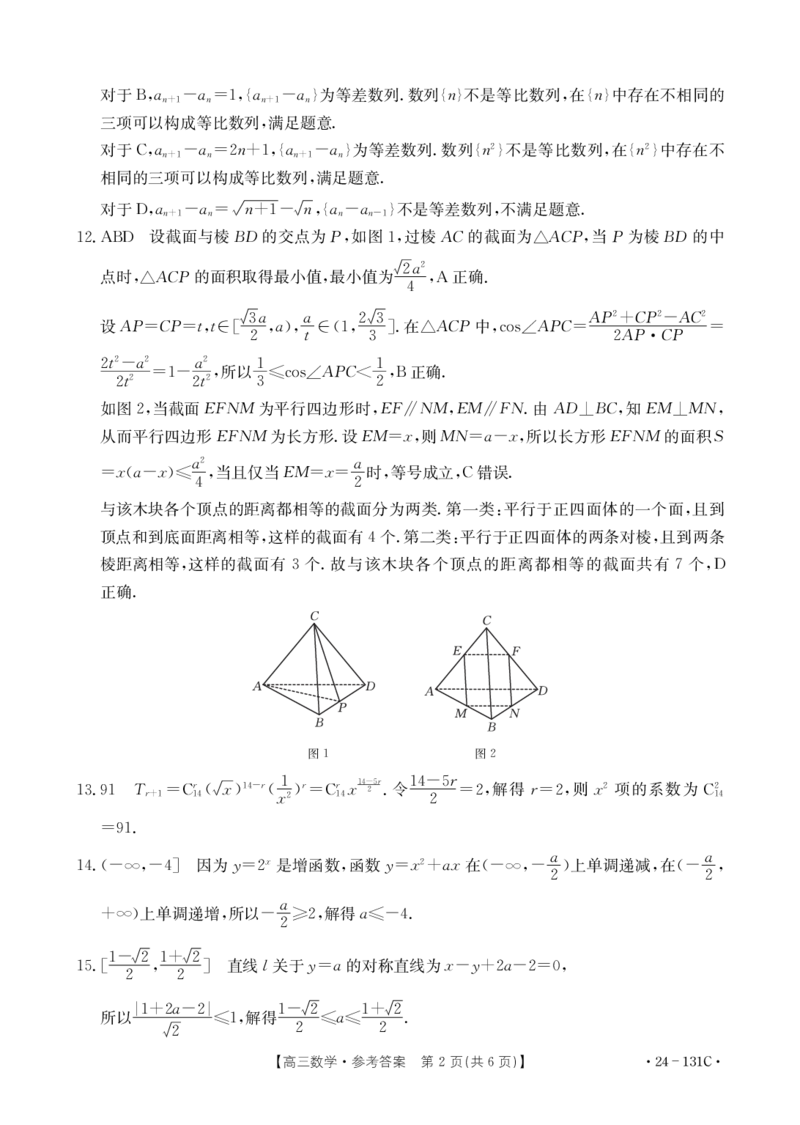
&
&*!"*%!!因为!为第一象限角"所以
"
为第四象限角!
)!3!当’$’"&$!时"满足’-&&("但不满足’&&(!若’’%"&’%"则’-&&&槡’&!因为’&
&("所以’-&&&槡’&&("即’-&&("当且仅当’$&$&时"等号成立!故&’-&&(’是&’&
&(’的必要不充分条件!
!
"!.!设圆台的高为+"则 +$!&-!4’-’&%$!’!"得+$’!故该圆台的母线与底面所成角的
’
’ ’
正切值为 $ !
’+! &
:0%!9
5!*!因为经过!%6过滤后消除了&%7的污染物"所以,8+!%*$9%7,"解得*$+ !
% % !%
当,$)%7, % 时")%7, % $, % 8 :0 ! % % !9-"解得-$+ : ! 0 %: % 0 !9 & $ &+ + :2 ! ; % ) (’!!
&
+,#+ +,.+
9!*!作,#)准线$图略%"则,#$.,"/,0*,/#$ $ !
+,/+ +,/+
+,/+
当 取最大值时"/,0*,/#取得最小值"当且仅当,/与抛物线相切于点,时"等号成
+,.+
立!当,/与抛物线相切时"设直线,/的方程为0$*1+!"代入1&$(0"可得1&+(*1-(
$%!由#$!"*&+!"$%"解得*$"+()!因为0$&1是增函数"函数0$1&-’1在$+>"+ %上单调递减"在$+ "
& &
’
->%上单调递增"所以+ &&"解得’.+(!
&
!+槡&!-槡&
!)!( " )!直线<关于0$’的对称直线为1+0-&’+&$%"
& &
+!-&’+&+ !+槡& !-槡&
所以 .!"解得 .’. !
槡& & &
!高三数学"参考答案!第!!!!&页#共"页$% "!"#$%$&"
{#{QQABCYQUggAgAABAAAhCAwHwCEIQkBCCCAoGAEAMIAIBQQFABAA=}#}/.
!"!(+&"")!因为/.$&"*($’%?"所以-/.(外接圆的半径=$ $
&/,0’%?
221 221
&"故(为-/.(外接圆上一动点!如图"当(位于(
!
时"/(在/.上的投影 $
! #
$
"
221 221 221
向量与/.方向相反"模长最大!当(位于( 时"/(在/.上的投影向量与
&
/ 221 .方向相同"模长最大!故/ 221 .*/ 221 (的取值范围为(+&"")! ! "
!5!解+$!%因为槡’&/,0&/$&’/,0."
所以&槡’/,0//,0.12//$&/,0//,0.!…………………………………………………&分
槡’
又/,0//,0.3%"所以槡’12//$!"即12//$ "………………………………………(分
’
槡"
因为/%$%"!%"所以/,0/$槡!+12/&/$ !…………………………………………)分
’
&槡’ &槡’
$&%由余弦定理知"’&$&&->&+&&>12//$&&->&+ &>&&&>+ &>"当且仅当&$>时"
’ ’
等号成立"……………………………………………………………………………………5分
&(
故&>. $!&-(槡’"…………………………………………………………………9分
’+槡’
! ! 槡"
则-/.(的面积9$ &>/,0/. 4$!&-(槡’%4 $&槡"-&槡&"…………………=分
& & ’
故-/.(的面积的最大值为&槡"-&槡&!………………………………………………!%分
4&-4
!9!解+$!%因为’&-’&-’&-,-’&$ $4%"4%"
! & ’ 4 &
$4+!%&-4+!
当4&&时"’&-’&-’&-,-’& $ $4%"4%"…………………………!分
! & ’ 4+! &
两式相减得’&$4"因为’’%"可得’$槡4"4&&"………………………………………’分
4 4 4
令4$!"可得’$!"满足’$槡4"…………………………………………………………)分
! 4
所以!’#的通项公式为’$槡4!……………………………………………………………"分
4 4
!
$&%&$ $槡4-!+槡4"
4
槡4-槡4-!
所以9$槡&+!-槡’+槡&-槡(+槡’-,-槡4-!+槡4$槡4-!+!!………………!&分
4
!=!解+$!%连接(6!因为/.$&"所以/6$!"(6$槡’!……………!分 ’ !
!
设( ! 7$(7$1"则67&$(7&-(6&$’-1&"/ ! 7&$/ ! (& ! -( ! 7&$( " ! % !
-1&"/6&$/6&-//&$!-(1&! ………………………………’分
! !
$
因为67)/7"所以67&-/7&$/6&"即’-1&-(-1&$!-(1&" !
! ! !
解得1$槡’! " # %
& (
故//$&1$&槡’!…………………………………………………)分
!
$&%以6为坐标原点"建立如图所示的空间直角坐标系"
!高三数学"参考答案!第!!!!’页#共"页$% "!"#$%$&"
{#{QQABCYQUggAgAABAAAhCAwHwCEIQkBCCCAoGAEAMIAIBQQFABAA=}#}则/$+!"%"&槡’%"7$%"槡’"槡’%"/$+!"%"%%"($%"槡’"%%"……………………………9分
!
221 221 221
6/$$+!"%"&槡’%"67$$%"槡’"槡’%"/($$!"槡’"%%!
!
设平面/67的法向量为!$$1"0"%%"
!
221
66/
!
*!$%" 6+1-&槡’%$%"
则5 即5 取%$!"则!$$&槡’"+!"!%!……………………!%分
221
767*!$%" 7槡’0-槡’%$%!
设直线/(与平面/67所成的角为$"
!
221
221 +!*/(+ 槡(&
则/,0$$+12/-!"/(.+$ 221 $ !
+!++/(+ &9
槡(&
故直线/(与平面/67所成角的正弦值为 !……………………………………!&分
! &9
&%!解+$!%前(个回合甲发球两次的情况分以下三种+
& ! & (
第一种情况"甲第!"&回合发球"乙第’"(回合发球"其概率为 4 4 $ !
’ ’ ’ &5
! ! ! !
第二种情况"甲第!"’回合发球"乙第&"(回合发球"其概率为 4 4 $ !
’ ’ ’ &5
! & ! &
第三种情况"甲第!"(回合发球"乙第&"’回合发球"其概率为 4 4 $ !
’ ’ ’ &5
( ! & 5
故前(个回合甲发球两次的概率为 - - $ !……………………………………(分
&5 &5 &5 &5
& !
$&%第&回合甲发球的概率为 "乙发球的概率为 !……………………………………)分
’ ’
& & ! ! ) & ! ! & (
第’回合甲发球的概率为 4 - 4 $ "乙发球的概率为 4 - 4 $ !…
’ ’ ’ ’ = ’ ’ ’ ’ =
……………………………………………………………………………………………5分
) & ( ! !(
第(个回合甲发球的概率为 4 - 4 $ !………………………………………9分
= ’ = ’ &5
$’%?可以取!"&"’"(!
! & & (
当?$!时",$ 4 4 $ /
! ’ ’ ’ &5
& 9
当?$(时",$$ %’$ /
( ’ &5
5
由$!%得"当?$&时",$ /
& &5
9
当?$’时",$!+,+,+,$ !…………………………………………………!%分
’ ! & ( &5
?的分布列为
? ! & ’ (
( 5 9 9
,
&5 &5 &5 &5
!高三数学"参考答案!第!!!!(页#共"页$% "!"#$%$&"
{#{QQABCYQUggAgAABAAAhCAwHwCEIQkBCCCAoGAEAMIAIBQQFABAA=}#}( 5 9 9 5(
7$?%$!4 -&4 -’4 -(4 $ ! …………………………………………!&分
&5 &5 &5 &5 &5
&!!解+$!%设,$1"0%"因为点,到直线1$(的距离是它到点"$!"%%的距离的&倍"
所以+1+(+$&槡$1+!%&-0&"则1&+91-!"$(1&+91-(-(0&"…………………’分
1& 0& 1& 0&
整理得 - $!"故曲线(的方程为 - $!!………………………………………)分
( ’ ( ’
61&
-
0&
$!"
$&%设/$1"0%".$1"0%"联立方程组5 ( ’
! ! & &
71$30+!"
整理得$’3&-(%0&+"30+=$%"…………………………………………………………"分
"3 =
则0-0$ "00$+ !……………………………………………………5分
! & ’3&-( ! & ’3&-(
! !&槡3&-!
因为<过点$+!"%%"所以9 $ 4&4+0+0+$槡$0-0%&+(00$
-"/. & ! & ! & ! & ’3&-(
!&
$ !……………………………………………………………………=分
!
’槡3&-!-
槡3&-!
! !
令-$槡3&-!"-&!"5$-%$’-- "则5@$-%$’+ ’%在(!"->%上恒成立"则5$-%&
- -&
!&
5$!%$("则 .’!……………………………………………………………………!!分
!
’--
-
故-"/.面积的最大值为’!……………………………………………………………!&分
&&!解+$!%5$1%的定义域为$%"->%!
&$’1&+&1+!%
5@$1%$ !……………………………………………………………………!分
1
当’.%时"’1&+&1+!/%在$%"->%上恒成立"即5@$1%/%"5$1%在$%"->%上单调递
减!……………………………………………………………………………………………&分
当’’%时"令’1&+&1+!$%"#$(-(’’%"
!-槡!-’ !+槡!-’
解得1$ ’%"1$ /%!
! ’ & ’
!-槡!-’ !-槡!-’
当1%$%" %时"5@$1%/%/当1%$ "->%时"5@$1%’%!
’ ’
!-槡!-’ !-槡!-’
故5$1%在$%" %上单调递减"在$ "->%上单调递增!……………(分
’ ’
综上"当’.%时"5$1%在$%"->%上单调递减/
!-槡!-’ !-槡!-’
当’’%时"5$1%在$%" %上单调递减"在$ "->%上单调递增! …)分
’ ’
$&%由$!%可得"当’.%时"5$1%在$%"->%上单调递减"5$1%最多只有!个零点! …"分
当’’%时"5$1%的最小值为5$1%!若5$1%有两个零点"则5$1%/%!………………5分
! !
!高三数学"参考答案!第!!!!)页#共"页$% "!"#$%$&"
{#{QQABCYQUggAgAABAAAhCAwHwCEIQkBCCCAoGAEAMIAIBQQFABAA=}#}&1-!
因为’1&+&1+!$%"所以’$ ! !
! ! 1&
!
’ &1-! &1-!
5$1%$’1&+(1+&:01- $&1-!+(1+&:01- ! $+&1+&:01- !
! ! ! ! ’ ! ! ! ’1& ! ! ’1&
! !
-!! …………………………………………………………………………………………9分
&1-! & &1-&
令函数A$1%$+&1+&:01- -!"A@$1%$+&+ + /%"
’1& 1 ’1’
所以A$1%在$%"->%上单调递减!
又因为A$!%$%"所以当1’!时"A$1%/%"则当1’!"即’%$%"’%时"5$1%/%!………
! !
…………………………………………………………………………………………!%分
!+1
令函数B$1%$:01+1-!"B@$1%$ !
1
当1%$%"!%时"B@$1%’%/当1%$!"->%时"B@$1%/%!
所以B$1%在$%"!%上单调递增"在$!"->%上单调递减"
所以B$1%.B$!%$%"即:01.1+!!
’ ’ ’
5$1%$’1&+(1+&:01- &’1&+(1-&+&1- $’1&+"1-&- !……………!!分
’ ’ ’
’ ’
令函数+$1%$’1&+"1-&- "+$%%$&- ’%"+$1%.5$1%/%!
’ ’ ! !
根据二次函数的图像及性质可得"81%$%"1%"+$1%’%"81%$1"->%"+$1%’%"
& ! & ’ ! ’
即81%$%"1%"5$1%’%"81%$1"->%"5$1%’%"
& ! & ’ ! ’
所以当1’!"即’%$%"’%时"5$1%有&个零点!
!
综上"若5$1%有两个零点"则’的取值范围为$%"’%! …………………………………!&分
!高三数学"参考答案!第!!!!"页#共"页$% "!"#$%$&"
{#{QQABCYQUggAgAABAAAhCAwHwCEIQkBCCCAoGAEAMIAIBQQFABAA=}#}