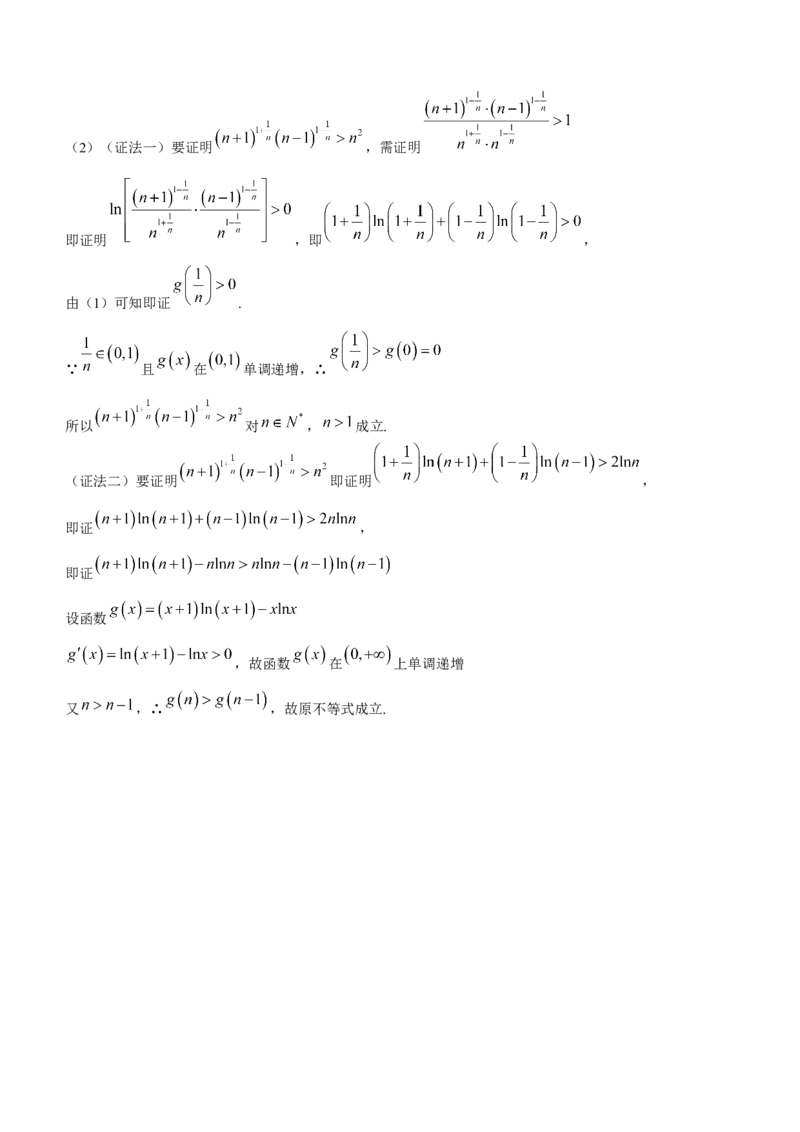文档内容
2023 年秋期高中三年级期中质量评估
数学试题
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分.考生做题时将答案答在答题卡的指
定位置上,在本试卷上答题无效。
2.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上
3.选择题答案使用2B铅笔填涂,非选择题答案使用 0.5毫米的黑色中性(签字)笔或碳素笔书
写,字体工整,笔迹清楚.
4.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.
5.保持卷面清洁,不折叠、不破损。
第I卷 选择题(共60分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的)
1.下列集合中,表示空集的是
A. B.
C. D.
2.命题“ , ”的否定为
A. , B. ,
C. , D. ,
3.若复数 满足 ,则
A. B.2 C. D.
4.公比不为1的等比数列 满足 ,若 ,则 的值为
A.8 B.9 C.10 D.11
5.若函数 有两个零点,则实数 的取值范围为
A. B. C. D.
6.已知 , , , ,则
学科网(北京)股份有限公司A. B. C. D.
7.已知 , , 分别为 的三个内角 , , 的对边,若点 在 的内部,且满足
,则称 为 的布洛卡(Brocard)点, 称为布洛卡角.布洛卡角满
足: (注: ).则
A. B. C. D.
8.已知 在 上单调递减,则实数 的取值范围为
A. B. C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
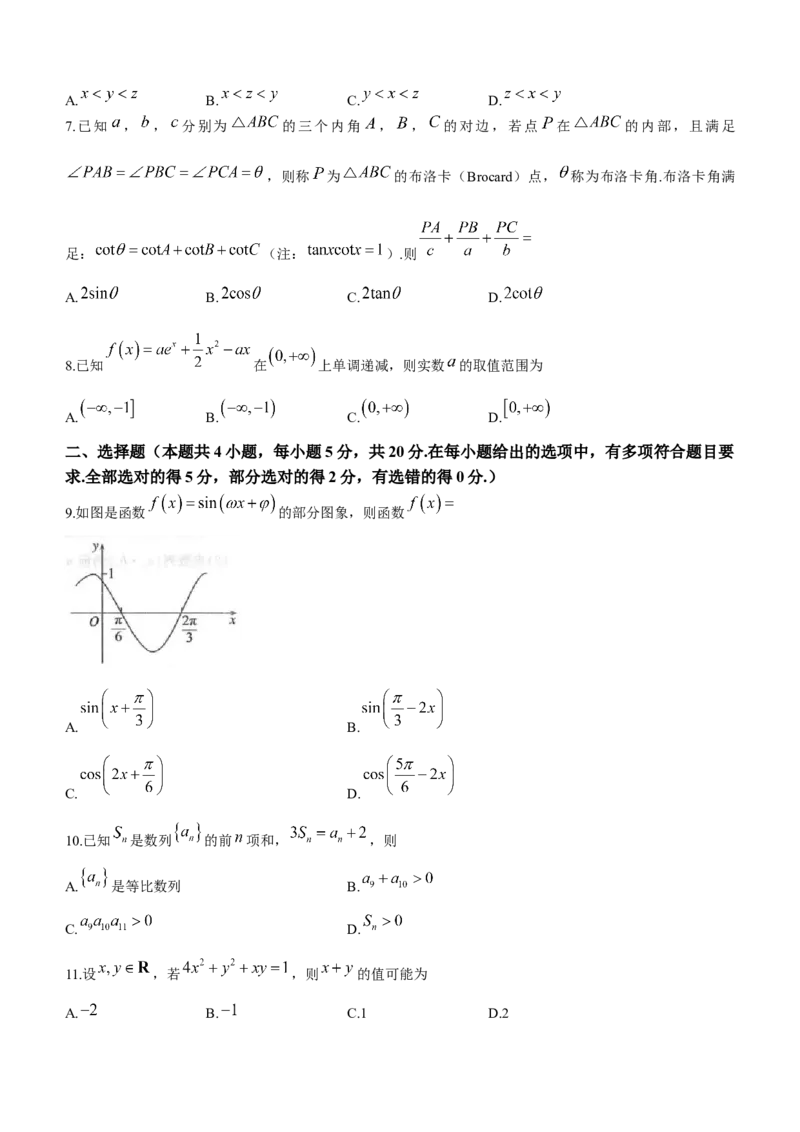
9.如图是函数 的部分图象,则函数
A. B.
C. D.
10.已知 是数列 的前 项和, ,则
A. 是等比数列 B.
C. D.
11.设 ,若 ,则 的值可能为
A. B. C.1 D.2
学科网(北京)股份有限公司12.设 ,若 为函数 的极小值点,则下列关系可能成立的是
A. 且 B. 且
C. 且 D. 且
第II卷 非选择题(共90分)
三、填空题(本题共4小题,每小题5分,共20分)
13.一个正实数的小数部分的2倍,整数部分和自身成等差数列,则这个正实数是______.
14.四边形 中, , , 是四边形 的外接圆的直径,则 ______.
15.奇函数 满足 , ,则 ______.
16.互不相等且均不为1的正数 , , 满足 是 , 的等比中项,则函数 的最小
值为______.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
设数列 为等差数列,其前 项和为 ,数列 为等比数列.已知 ,
, .
(1)求数列 和 的通项公式;
(2)求数列 的前 项和 .
18.(本小题满分12分)
已知函数 ,其中 ,若实数 , 满足 时,
的最小值为 .
(1)求 的值及 的单调递减区间;
(2)若不等式 对任意 时恒成立,求实数 的取值范
围.
19.(本小题满分12分)
学科网(北京)股份有限公司记 为数列 的前 项和.已知 .
(1)证明: 是等差数列;
(2)若 , , 成等比数列,求数列 的前2024项的和.
20.(本小题满分12分)
在 中,角 , , 的对边分别为 , , ,且满足_____.
(从以下两个条件中任选一个补充在上面横线上作为已知,将其序号写在答题卡的横线上并作答.)
条件①:
条件②:
(1)求角 ;
(2)若 为锐角三角形, ,求 面积的取值范围.
21.(本小题满分12分)
已知函数 , , ,曲线 在点 处的切线也是曲线
的切线.
(1)若 ,求 ;
(2)求 的取值范围.
22.(本小题满分12分)
(1)已知函数 ,判断函数 的单调性并证明;
(2)设 为大于1的整数,证明: .
2023 年秋期高中三年级期中质量评估
数学参考答案
一.选择题:
1-8.BADC CDBA
学科网(北京)股份有限公司二.选择题:
9.BC 10.ABD 11.BC 12.AC
三.填空题:
13. 或 14. 15. 16.4
四.解答题:
17.解:(1)设等差数列 的公差为 ,等比数列 的公比为 ,
由 可得 ,
即 ,解得 ,
所以, ,
,∴
则 ;
(2) ,
则 ①,
可得 ②,
① ②得:
,
因此,
18.解:(1)
学科网(北京)股份有限公司因为实数 , 满足 时, 的最小值为 .
所以 的最小正周期 ,解得 ,
所以 ,由 ,得
的单调递减区间为
(2)不等式 对任意 时恒成立,
,
令 , ,∴
,
, 恒成立
令 ,
∴ ,解得: ,
学科网(北京)股份有限公司故实数 的取值范围是
19.解:(1)因为 ,即 ①,
当 时, ②,
① ②得, ,
即 ,
即 ,所以 , 且 ,
所以 是以1为公差的等差数列.
(2)由(1)可得 ,
又 , , 成等比数列,所以 ,解得 ,
所以
∴ .
∴数列 的前2024项和为:
20.解:解析:(1)选择条件①:
由题意及正弦定理知 ,
∴ ,∴
∵ ,∴ .
学科网(北京)股份有限公司选择条件②:因为 ,所以 ,
即 ,解得 ,又 ,
所以
(2)由 可得
因为 是锐角三角形,由(1)知 , 得到 ,
故 ,解得 ,所以 .
,
21.解:(1)由题意知, , , ,
则 在点 处的切线方程为 ,
设该切线与 切于点 , ,则 ,解得 ,
则 ,解得 ;
(2)因为 ,则 在点 处的切线方程为 ,
学科网(北京)股份有限公司整理得 ,
设该切线与 切于点 , ,则 ,
则切线方程为 ,整理得 ,
则 ,整理得 ,
令 ,则 ,
令 ,解得 或 ,
令 ,解得 或 ,
则 变化时, , 的变化情况如下表:
0 1
- 0 + 0 - 0 +
则 的值域为 ,故 的取值范围为
22.解:(1)函数 的定义域为 ,函数 的定义域为
函数 在 上单调递减,
在 上单调递增
证明: ,∴
所以 为 上的偶函数.
对 恒成立.
所以函数 在 上单调递减,在 上单调递增
学科网(北京)股份有限公司(2)(证法一)要证明 ,需证明
即证明 ,即 ,
由(1)可知即证 .
∵ 且 在 单调递增,∴
所以 对 , 成立.
(证法二)要证明 即证明 ,
即证 ,
即证
设函数
,故函数 在 上单调递增
又 ,∴ ,故原不等式成立.
学科网(北京)股份有限公司