数学试题_2024-2025高二（7-7月题库）_2024年11月试卷_1127重庆市万州二中2024-2025学年高二上学期期中考试_重庆市万州二中2024-2025学年高二上学期期中考试数学试题（PDF版，含答案）

万州二中高 2023 级高二上期中考数学试题 命题人:张春 审题人：张应红 考生注意： 1.本试卷分选择题和非选择题两部分.满分150分，考试时间 120分钟. 2.答题前，考生务必用直径 0.5毫米黑色墨水签字笔将密封线内项目填写清楚. 3.考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用2B 铅笔把答题卡上对应 题目的答案标号涂黑；非选择题请用直径 0.5毫米黑色墨水签字笔在题卡上各题的答题区域内 作答，超出答题区域书写的答案无效，在试题卷､草稿纸上作答无效. 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1. 直线x 3y20的倾斜角为（ ） A. 150 B. 120 C. 60o D. 30o 2. 已知圆C的方程是x2  y2 4x2y110，则圆心C的坐标是（ ） A. 2,1  B.  2,1  C. 4,2  D.  4,2  x2 y2 3. 设F,F 是双曲线C： - =1的左、右焦点，过F 的直线与C的右支交于P，Q两点，则 1 2 4 3 2 |FP||FQ||PQ|（ ） 1 1 A. 5 B. 6 C. 8 D. 12 4. 两平行直线l ：x2y 10 0，l ：2x4y3 10 0之间的距离为（ ） 1 2 5 2 A. B. 3 C. 5 D. 2 2 2 5. 已知圆M :(x1)2 (y2)2 1与圆N：(x3)2 (y4)2 1关于直线l对称，则l的方程为（ ） A. x2y50 B. x2y50 C 2x y50 D. 2x y50 . 1    6. 已知向量a(2,3,0)，b (0,3,4)，则向量a在向量b 上的投影向量的坐标为（ ）  18 27  18 27  A.   , ,0 B.  , ,0  13 13  13 13   27 36  27 36 C. 0, ,  D. 0, ,   25 25  25 25 7. 已知圆C:x2  y2 8x120，点P在圆C上，点A  6,0  ，M 为AP的中点，O为坐标原点，则 tanMOA的最大值为（ ） 6 7 6 6 A. B. C. D. 12 12 4 3 8.已知点 P 为直线l :mx2ym60 与直线l :2xmym60(mR) 的交点，点Q 为圆 1 2 C :(x3)2 (y3)2 8 上的动点，则|PQ| 的取值范围为( )  A.2 2,8 2 B. 2 2,8 2     C. 2,6 2 D. 2,6 2    二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9. 若直线a2x4ya 0与直线  a2  x  a2 2a4  y20平行，则a的值可以是（ ） A. 0 B. 2 C. 2 D. 4 10. 已知正方体ABCDABC D 的棱长为2，若AA ，BC的中点分别为M ，N ，则（ ） 1 1 1 1 1 A MN CC B. 平面ABC //平面ADC . 1 1 1 1 8 29 C. BN  DM D. 点D到平面DMN 的距离为 1 1 1 29 11. 已知点P  x ,y  ，直线l:x x y y1及圆C:x2  y2 1，则下列结论正确的是（ ） 0 0 0 0 A. 若点P在C上，则l与C相切 3 B. 若点P在圆x2  y2 4上，则l被圆C截得的弦长为 2 C. 若点P在圆C外，过点P作圆C的切线，则l为过两切点的直线 D. 若点P在圆C内，过点P的直线与圆C交于点M,N ，则圆C在M,N 处的切线的交点在l上 2三､填空题：本题共 3小题，每小题 5分，共 15分. 12. 设向量a   1,2,m  ,b   2,0,1  ，若a  b  ，则m__________. x2 y2 13. 已知椭圆C:  1(a b 0)左､右焦点分别为F､F，过F且倾斜角为30°的直线l与过F的直线 1 2 1 1 2 a2 b2 l交于P点，点P在椭圆上，且∠FPF=90°.则椭圆C的离心率e=___________. 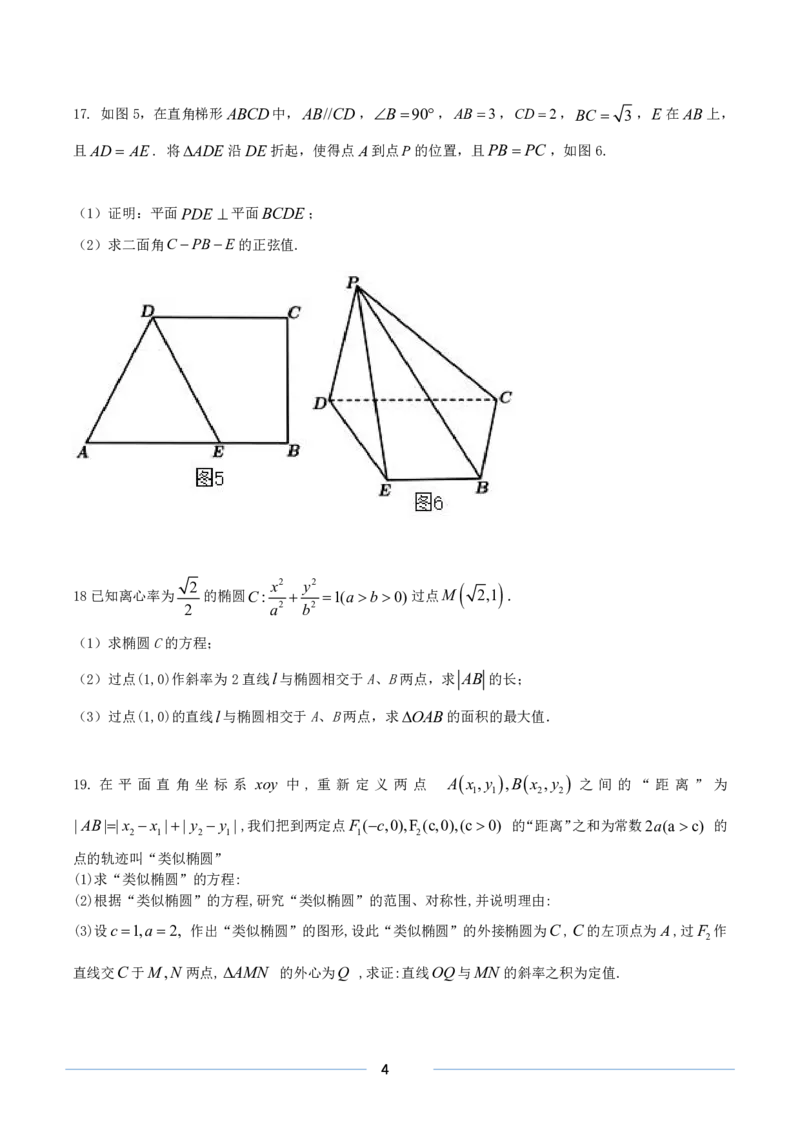2 1 2 14.我国南北朝时期的著名数学家祖原提出了祖眶原理："幂势既同，则积不容异．"意思是，夹在两个平行 平面之间的两个几何体，被平行于这两个平面的任意一个平面所截，若截面面积都相等，则这两个几何体 的体积相等，运用祖原理计算球的体积时，构造一个底面半径和高都与球的半径相等的圆柱，与半球（如 图①）放置在同一平面上，然后在圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥后 得到一新几何体（如图②)，用任何一个平行于底面的平面去截它们时，可证得所截得的两个截面面积相等， 1 1 2 x2 y2 由此可证明新几何体与半球体积相等，即 V =R2R R2R  R3,现将椭圆  1 绕y 球 2 3 3 4 9 轴旋转一周后得一橄榄状的几何体（如图③)，类比上述方法，运用祖眶原理可求得其体积等于_________ 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 15. 已知直线l： 2a1  x a1  ya50. （1）若直线l与直线l：x2y10平行，求a的值； （2）若直线l在两坐标轴上的截距相等，求直线l的方程. 16. 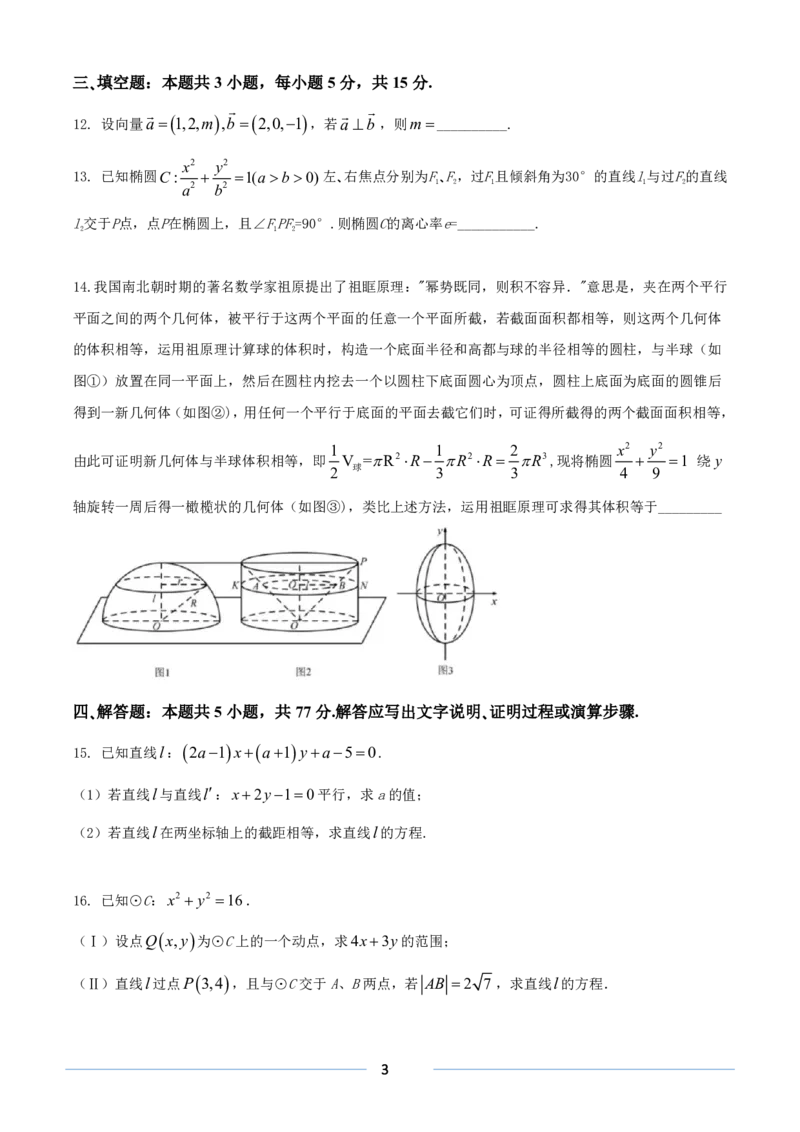已知⊙C：x2  y2 16． （Ⅰ）设点Q  x,y 为⊙C上的一个动点，求4x3y的范围； （Ⅱ）直线l过点P  3,4 ，且与⊙C交于A、B两点，若 AB 2 7 ，求直线l的方程． 317. 如图5，在直角梯形ABCD中，AB//CD，B90，AB3，CD2，BC  3 ，E在AB上， 且AD AE. 将ADE 沿DE折起，使得点A到点P的位置，且PB PC，如图6. （1）证明：平面PDE 平面BCDE； （2）求二面角CPBE的正弦值. 2 x2 y2   18已知离心率为 的椭圆C:  1(a b 0)过点M 2,1 ． 2 a2 b2 （1）求椭圆C的方程； （2）过点(1,0)作斜率为2直线l与椭圆相交于A、B两点，求 AB 的长； （3）过点(1,0)的直线l与椭圆相交于A、B两点，求OAB的面积的最大值． 19. 在 平 面 直 角 坐 标 系 xoy 中 , 重 新 定 义 两 点 A  x ,y  ,B  x ,y  之 间 的 “ 距 离 ” 为 1 1 2 2 | AB||x x || y  y |,我们把到两定点F(c,0),F (c,0),(c0) 的“距离”之和为常数2a(a c) 的 2 1 2 1 1 2 点的轨迹叫“类似椭圆” (1)求“类似椭圆”的方程: (2)根据“类似椭圆”的方程,研究“类似椭圆”的范围、对称性,并说明理由: (3)设c 1,a 2, 作出“类似椭圆”的图形,设此“类似椭圆”的外接椭圆为C,C的左顶点为A,过F 作 2 直线交C于M,N 两点,AMN 的外心为Q ,求证:直线OQ与MN 的斜率之积为定值. 4