数学试题_2024-2025高二（7-7月题库）_2024年12月试卷_1205浙江省六校联盟2024-2025学年高二期中联考_浙江省六校联盟2024-2025学年高二上学期期中联考数学试题

保密★考试结束前 六校联盟2024学年第一学期期中联考 (2024.11) 高二数学试题卷 命题、审题：台州市金清中学(汪德富) 温岭市松门中学(吴志康) 考生须知： 1.本试题卷分选择题和非选择题两部分.全卷共4页，满分150分，考试时间120分钟. 2.考生答题前，务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上. 选择题部分 一、选择题(本题共8小题，每小题5分，共40分。每小题列出的四个备选项中只有一个是符合题目要求 的，不选、多选、错选均不得分) 1.直线 3xy30的倾斜角为( ) A.30° B.60° C.120° D.150° x2 2.已知双曲线方程为 y2 1，则其焦距2c=( ) 3 A.2 3 B.2 2 C.2 D.4 3.若平面a的一个法向量n2，2,1，点 A1,3,0 在平面a内，则点 P2,1,4到平面a的距离 ( ) 8 10 A.3 B.10 C. D. 3 3 4.已知圆C :x2(y1)2 9与圆C :(x2 3)2(y1)2 1的位置关系为( ) 1 2 A.相离 B.相交 C.外切 D.内切 5.已知直线l经过两条直线l ：xy2， l ：2xy1的交点，且l的一个方向向量为v2,3，则 1 2 直线l的方程为( ) A.2x3y50 B.3x2y50 C.3x2y50 D.2x 3y 1 0 x2 y2 6.已知双曲线  1(a0,b0)的左右焦点分别为F,F ，且 FF 2，当点F 到渐近线的距离 a2 b2 1 2 1 2 2 1 为 时，该双曲线的离心率e为( ) 2 3 4 2 3 A. B. C.2 3 D. 3 3 3 x2 y2 7.已知点M在椭圆C:  1上运动，圆C的圆心为椭圆的右焦点，半径r1，过点M引直线l,l 25 16 1 2 与圆C相切，切点分别为P，Q，则|PQ|的取值范围为( )  3 7   3 7 4 7  A.  2, 4    B.  3, 4   C.  7 ,2    D.[ 3,4) 六校联盟期中联考【高二数学】试题卷(第1页,共4页) {#{QQABCYaEoggAAAAAAAgCAwFyCEKQkgACCSgOAFAEoAAASRNABAA=}#}8.在三棱锥DABC中，ABBC，AB= 3,BC=1,若AD为三棱锥DABC的外接球直径，且AC与BD 5 所成角的余弦值为 ，则该外接球的表面积为( ) 10 A.8π B.6π C.5π D.16π 二、选择题(本题共3小题，每小题6分，共18分。每小题列出的四个备选项中至少有一个是符合题目要 求的。全部选对的得6分，部分选对得部分分，有选错的得0分) 9.下列说法正确的是( ) A.空间中的三个向量，若有两个向量共线，则这三个向量一定共面 B.直线l的方向向量a0,3,6，平面a的法向量n1,2,1，则l C.已知直线l经过点A1,2,1,B0,1,1，则P1,2,2到l的距离为 3 D.若ab0，则 a,b 为钝角 10.已知直线l：kx2k1y3k20，则下列选项正确的是( ) 1 A.当直线l与直线xy20平行时，k  3 B.当直线l与直线xy20垂直时，k 1 C.当实数k变化时，直线l恒过点1,2 D.直线l和x,y负半轴构成的三角形面积最小值是4 11.如图，在长方体 ABCDABCD 中， AB AA 5,AD3，点P是平面 ABCD上的动点，满足 1 1 1 1 1 BD BP， D C 1 1 1 1 A.P在底面ABCD上的轨迹是一条直线 A 1 B 1 B.三棱锥PABC 的体积是定值 1 1 1 D 5 34 C.若角是直线DP和平面ABCD所成角，则tan的最大值是 P C 1 9 A B D.不存在点P，使得PD PC 1 非选择题部分 三、填空题(本题共3小题，每小题5分，共15分) 12.向量a1,x,4与b2x,8,y共线，且方向相同，则xy＝ . y2 13.设F，F 是双曲线x2 1的两个焦点，P是双曲线上的一点，且4PF 3PF ，则PFF 的面积 1 2 24 1 2 1 2 等于 . 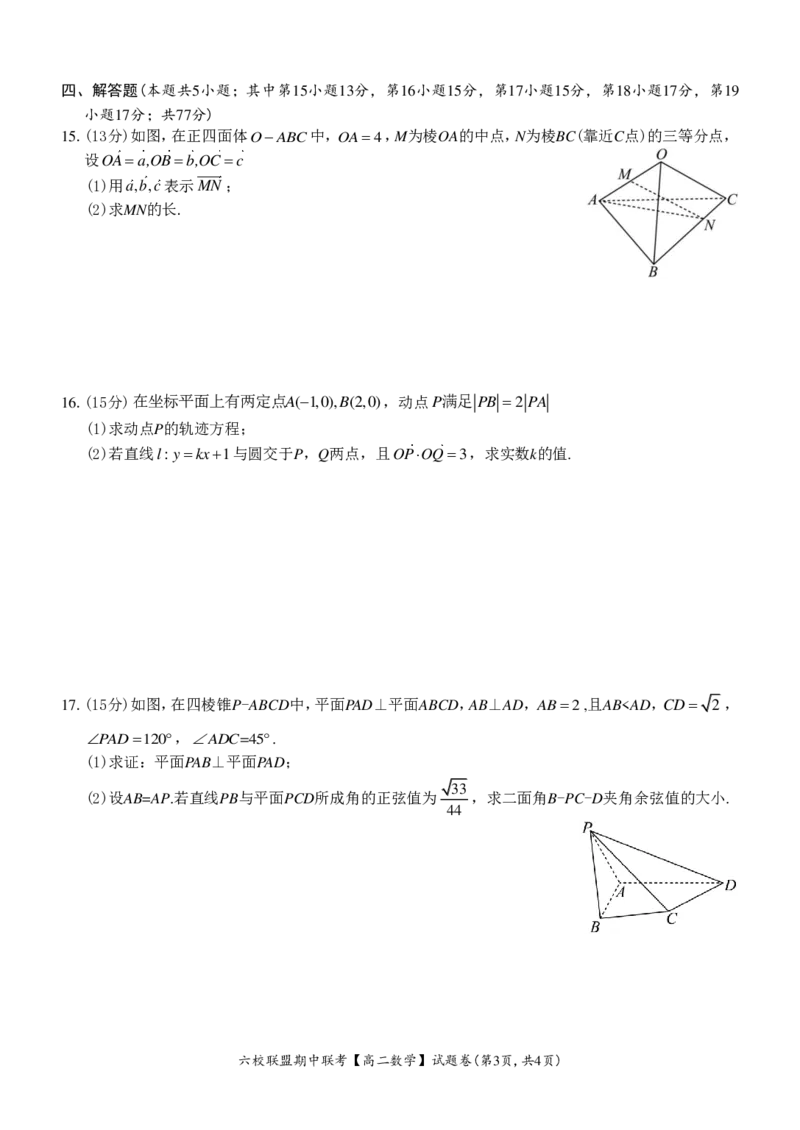14.圆和圆锥曲线的关系十分密切，它们有很多相似的结论.例如，过圆x2y2 r2上任意不同两点作 圆的切线，如果切线垂直且相交于P点，则动点P的轨迹为圆.在椭圆中也有类似的结论.已知椭圆 x2 C： y2 1，过椭圆C上任意不同两点作椭圆的切线，若两切线垂直且相交于P点，则动点P的轨 2 迹方程是 ． 六校联盟期中联考【高二数学】试题卷(第2页,共4页) {#{QQABCYaEoggAAAAAAAgCAwFyCEKQkgACCSgOAFAEoAAASRNABAA=}#}四、解答题(本题共5小题；其中第15小题13分，第16小题15分，第17小题15分，第18小题17分，第19 小题17分；共77分) 15.(13分)如图，在正四面体OABC中，OA4，M为棱OA的中点，N为棱BC(靠近C点)的三等分点， 设OAa,OBb,OCc (1)用a,b,c表示MN； (2)求MN的长. 16.(15分)在坐标平面上有两定点A(1,0),B(2,0)，动点P满足PB 2 PA (1)求动点P的轨迹方程； (2)若直线l:ykx1与圆交于P，Q两点，且OPOQ3，求实数k的值. 17.(15分)如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB⊥AD，AB2,且AB