数学试题_2024-2025高二（7-7月题库）_2024年11月试卷_1123四川省南充市嘉陵一中2024-2025学年高二上学期第二次月考（11月）

嘉陵一中高 2023 级高二上期中考试 数学试卷 考试时间：120分钟，满分150分 注意事项： 1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上 一、选择题：（本题共8小题，每小题5分，共40分。每小题给出的四个选项中，只有一项是符合题目要求的） 1．直线x 3y20的倾斜角为（ ） π 5π 3 A． B． C． 3 D． 3 6 3 2．已知圆C ：x2  y2 4，圆C ：x2  y2 4x4y40，则两圆的公共弦所在直线的方程为（ ） 1 2 A．xy20 B．xy20 C．x y40 D．x y40 3．平面内，动点P的坐标x,y满足方程  x 3 2 y2  x 3 2 y2 2 6 ，则动点P的轨迹方程为（ ） x2 y2 x2 y2 A．  1 B．  1 24 21 6 3 x2 y2 x2 y2 C．  1 D．  1 6 9 9 6 4．“a3”是“直线l :a1x2y10与直线l :3xay10 平行”的（ ） 1 2 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 x2 y2 5．已知F,F 是椭圆C:  1的两个焦点，点P在C上，且 PF 3，则PFF 的面积为（ ） 1 2 2 1 2 16 12 A．3 B．4 C．6 D．10 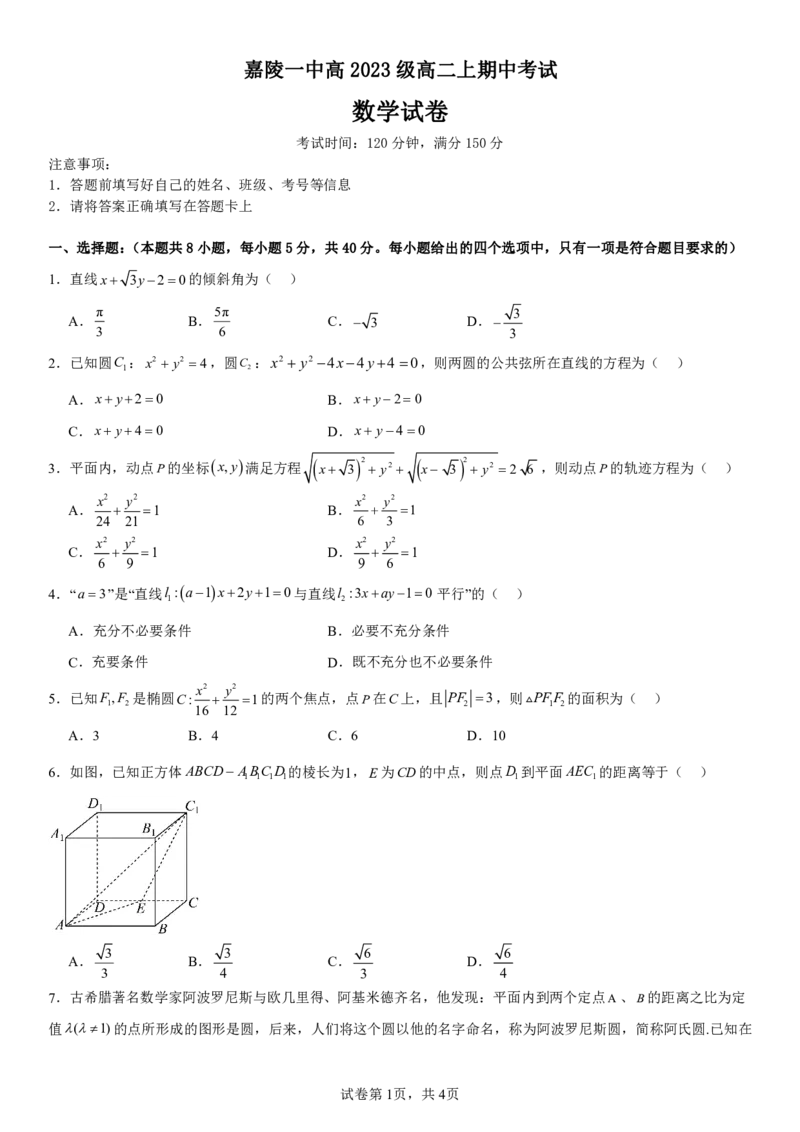6．如图，已知正方体ABCD ABCD的棱长为1，E为CD的中点，则点D 到平面AEC 的距离等于（ ） 1 1 1 1 1 1 3 3 6 6 A． B． C． D． 3 4 3 4 7．古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名，他发现：平面内到两个定点A、B的距离之比为定 值(1)的点所形成的图形是圆，后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆.已知在 试卷第1页，共4页|PA| 1 平面直角坐标系xOy中，A(2,0)，B(4,0).点P满足  ，设点P所构成的曲线为C，下列结论不正确的是（ ） |PB| 2 A．C的方程为(x4)2y2 16 B．在C上存在点D，使得D到点(1,1)的距离为3 C．在C上存在点M ，使得|MO|2|MA| D．C上的点到直线3x4y130的最小距离为1 1 8．x,yR，函数 f x,y x12y42  3x4y5 的最小值为（ ） 5 12 14 16 A．2 B． C． D． 5 5 5 二、多选题：（本题共3小题，每小题6分，共18分。每小题给出的四个选项中，有多项符合题目要求。全部选对 得6分，部分选对得部分分，有选错得0分） 9．对于随机事件A和事件B，PA0.3，PB0.4，则下列说法正确的是（ ） A．若A与B互斥，则PAB0.3 B．若A与B互斥，则PAB0.7 C．若A与B相互独立，则PAB0.12 D．若A与B相互独立，则PAB0.7 10．关于空间向量，以下说法正确的是（ ）   A．若直线l的方向向量为m2,4,2，平面的一个法向量为n1,2,1，则l  1 1 1 B．若空间中任意一点O，有OP OA OB OC ，则P,A,B,C四点共面 3 6 2       C．若空间向量a，b满足ab 0，则a与b夹角为钝角 D．若空间向量a  1,0,1，b  0,1,1，则a  在b  上的投影向量为  0, 1 , 1   2 2 11．伊帕姆维泽蒂博物馆收藏的达・芬奇方砖，在正六边形上画了正方体图案，如图1，把三片这样的达・芬奇方砖 拼成图2的组合，这个组合再转换成图3所示的几何体.若图3中每个正方体的棱长为1，则（ ）    2 A. CG2AA 2PF B. 直线CQ与平面ABCD 所成角的正弦值为 1 1 1 1 1 3 3 5 C.异面直线CQ与BD所成角的余弦值为 D．点C 到直线CQ的距离是 1 6 3 试卷第2页，共4页三、填空题：（本题共3小题，每小题5分，共15分）      12．已知向量a2,1,3，b1,2,1，若a  ab  ，则 . 13．已知两点A(3，4)，B(3，2)，过点P(1，0)的直线l与线段AB有公共点，则直线l的斜率k的取值范围是 . 14．已知圆O的方程为x2y2 2，点P是直线x2y50上的一个动点，过点P作圆O的两条切线PA,PB,A,B为 切点，则四边形PAOB面积的最小值为 ；直线AB过定点 . 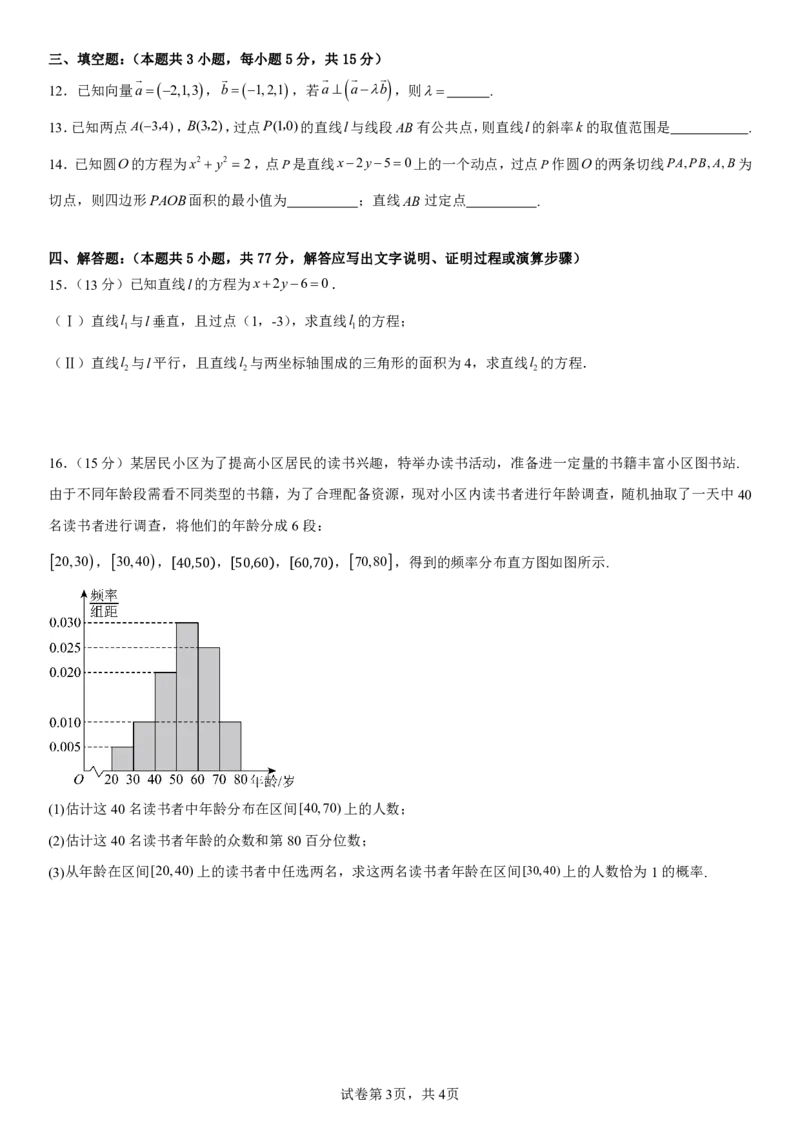四、解答题：（本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤） 15．（13分）已知直线l的方程为x2y60． （Ⅰ）直线l 与l垂直，且过点（1，-3），求直线l 的方程； 1 1 （Ⅱ）直线l 与l平行，且直线l 与两坐标轴围成的三角形的面积为4，求直线l 的方程． 2 2 2 16．（15分）某居民小区为了提高小区居民的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站. 由于不同年龄段需看不同类型的书籍，为了合理配备资源，现对小区内读书者进行年龄调查，随机抽取了一天中40 名读书者进行调查，将他们的年龄分成6段：  20,30， 30,40， ， ， ，70,80，得到的频率分布直方图如图所示. ᴘ᜽ꡰᴘ ꡰᴘ᜽ᴘ ᴘ᜽ᴘ (1)估计这40名读书者中年龄分布在区间[40,70)上的人数； (2)估计这40名读书者年龄的众数和第80百分位数； (3)从年龄在区间[20,40)上的读书者中任选两名，求这两名读书者年龄在区间[30,40)上的人数恰为1的概率. 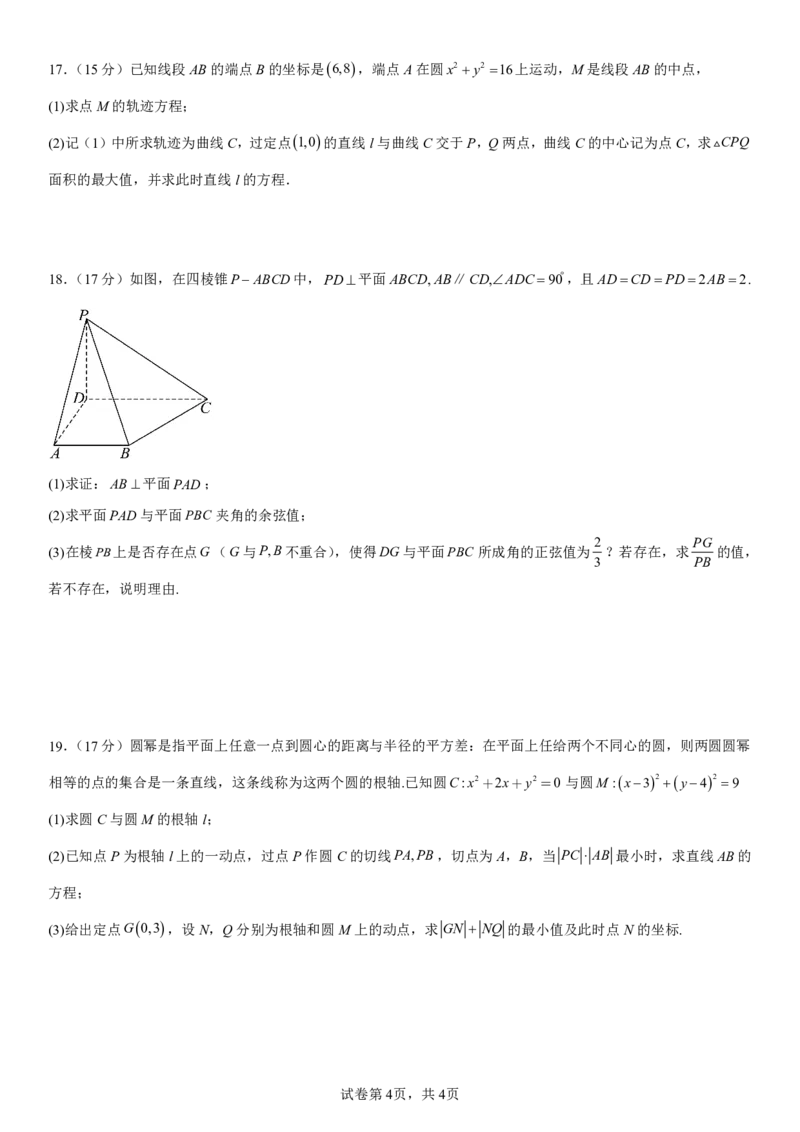试卷第3页，共4页17．（15分）已知线段AB的端点B的坐标是6,8，端点A在圆x2y2 16上运动，M是线段AB的中点， (1)求点M的轨迹方程； (2)记（1）中所求轨迹为曲线C，过定点1,0的直线l与曲线C交于P，Q两点，曲线C的中心记为点C，求CPQ 面积的最大值，并求此时直线l的方程． 18．（17分）如图，在四棱锥PABCD中，PD平面ABCD,AB∥CD,ADC 90，且ADCDPD2AB2. (1)求证：AB平面PAD； (2)求平面PAD与平面PBC 夹角的余弦值； 2 PG (3)在棱PB上是否存在点G（G与P,B不重合），使得DG与平面PBC 所成角的正弦值为 ？若存在，求 的值， 3 PB 若不存在，说明理由. 19．（17分）圆幂是指平面上任意一点到圆心的距离与半径的平方差：在平面上任给两个不同心的圆，则两圆圆幂 相等的点的集合是一条直线，这条线称为这两个圆的根轴.已知圆C:x2+2x+y2 =0 与圆M :x32y42 9 (1)求圆C与圆M的根轴l； (2)已知点P为根轴l上的一动点，过点P作圆C的切线PA,PB，切点为A，B，当 PC  AB 最小时，求直线AB的 方程； (3)给出定点G0,3，设N，Q分别为根轴和圆M上的动点，求GN  NQ 的最小值及此时点N的坐标. 试卷第4页，共4页