文档内容
2024-2025 学年高二第一学期第一次月考数学科试题
一、单选题(本大题共8小题,每小题5分,共40分.每小题给出的四个选项中,只有一个选
项是正确的.请把正确的选项填涂在答题卡相应的位置上.)
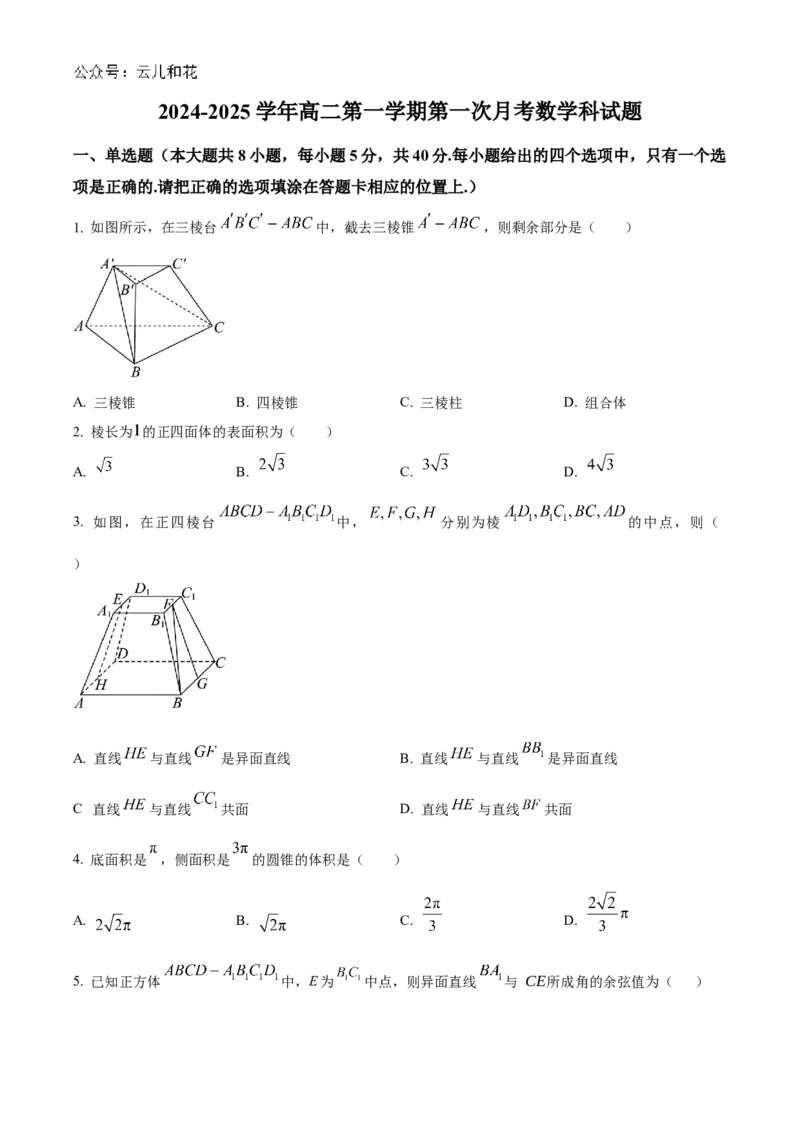
1. 如图所示,在三棱台 中,截去三棱锥 ,则剩余部分是( )
A. 三棱锥 B. 四棱锥 C. 三棱柱 D. 组合体
2. 棱长为 的正四面体的表面积为( )
A. B. C. D.
3. 如图,在正四棱台 中, 分别为棱 的中点,则(
)
A. 直线 与直线 是异面直线 B. 直线 与直线 是异面直线
.
C 直线 与直线 共面 D. 直线 与直线 共面
4. 底面积是 ,侧面积是 的圆锥的体积是( )
A. B. C. D.
5. 已知正方体 中,E为 中点,则异面直线 与 CE所成角的余弦值为( )A. B. C. D.
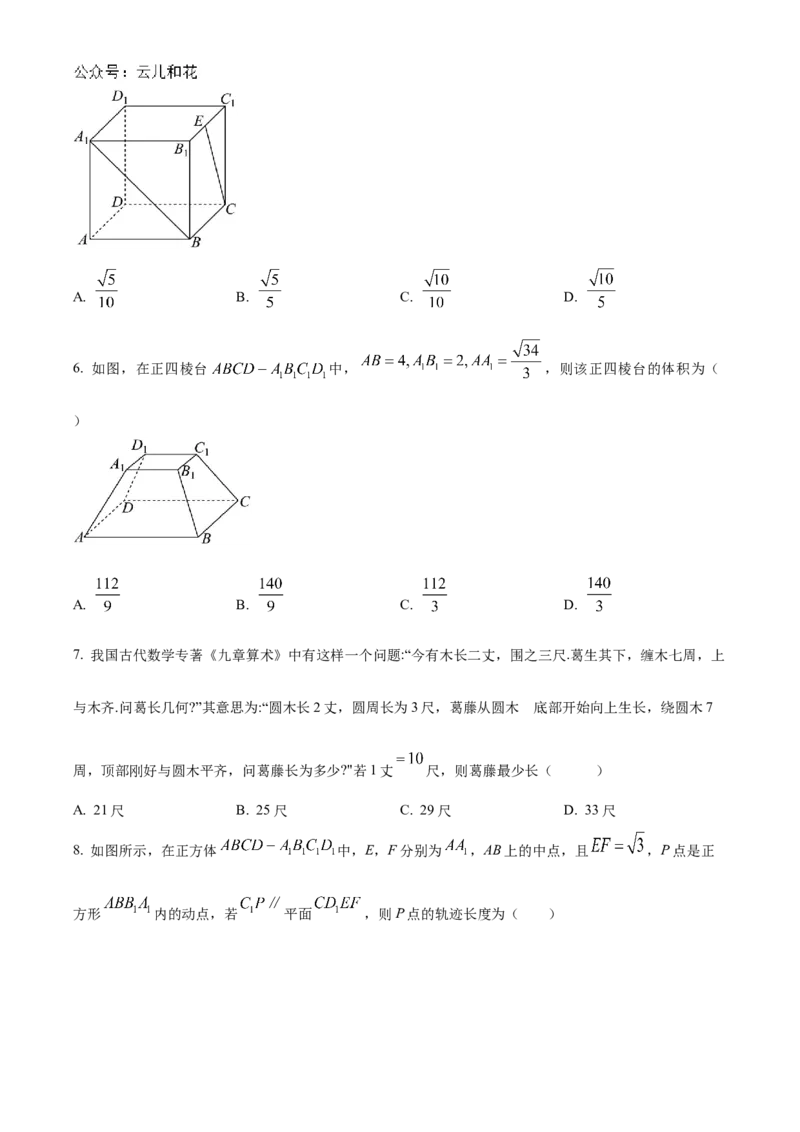
6. 如图,在正四棱台 中, ,则该正四棱台的体积为(
)
A. B. C. D.
7. 我国古代数学专著《九章算术》中有这样一个问题:“今有木长二丈,围之三尺.葛生其下,缠木七周,上
的
与木齐.问葛长几何?”其意思为:“圆木长2丈,圆周长为3尺,葛藤从圆木 底部开始向上生长,绕圆木7
周,顶部刚好与圆木平齐,问葛藤长为多少?"若1丈 尺,则葛藤最少长( )
A. 21尺 B. 25尺 C. 29尺 D. 33尺
8. 如图所示,在正方体 中,E,F分别为 ,AB上的中点,且 ,P点是正
方形 内的动点,若 平面 ,则P点的轨迹长度为( )A. B. C. D.
二、多选题(本大题共3小题,每小题6分,共计18分.每小题给出的四个选项中,有多项符
合题目要求.全部选对得6分,选对但不全的部分分,有选错的得0分.)
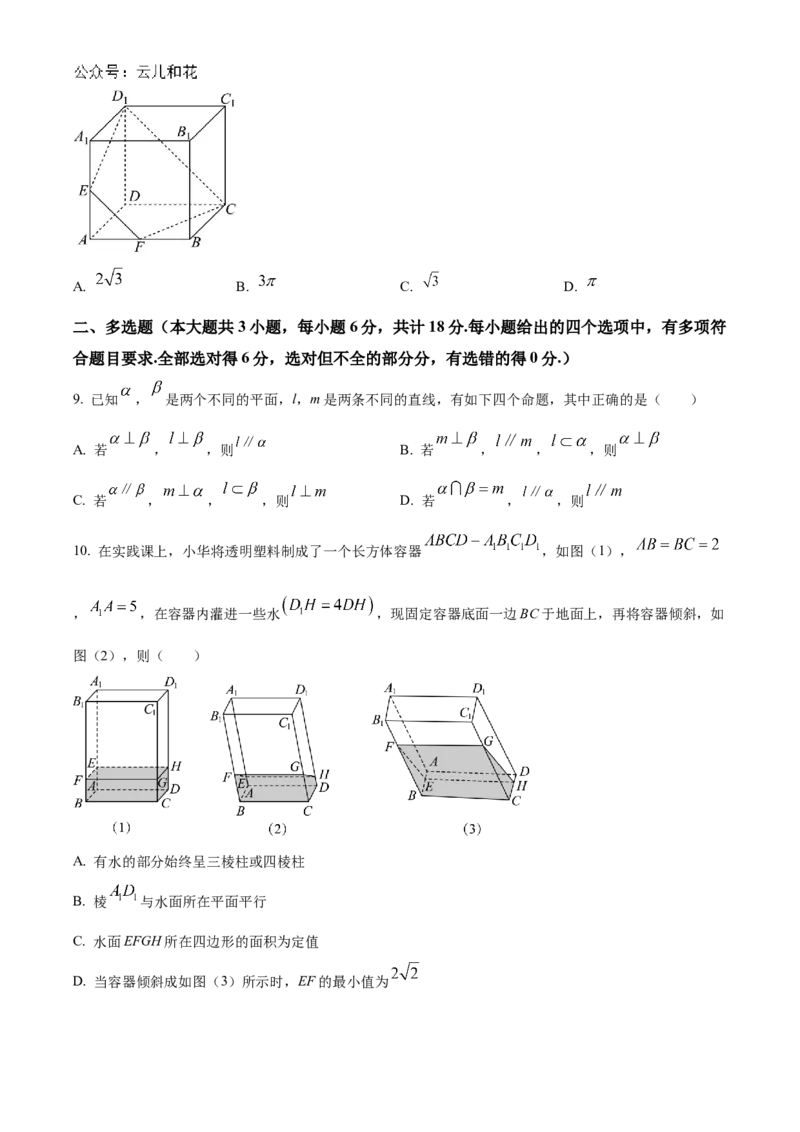
9. 已知 , 是两个不同的平面,l,m是两条不同的直线,有如下四个命题,其中正确的是( )
A. 若 , ,则 B. 若 , , ,则
C. 若 , , ,则 D. 若 , ,则
10. 在实践课上,小华将透明塑料制成了一个长方体容器 ,如图(1),
, ,在容器内灌进一些水 ,现固定容器底面一边BC于地面上,再将容器倾斜,如
图(2),则( )
A. 有水的部分始终呈三棱柱或四棱柱
B. 棱 与水面所在平面平行
C. 水面EFGH所在四边形的面积为定值
D. 当容器倾斜成如图(3)所示时,EF的最小值为的
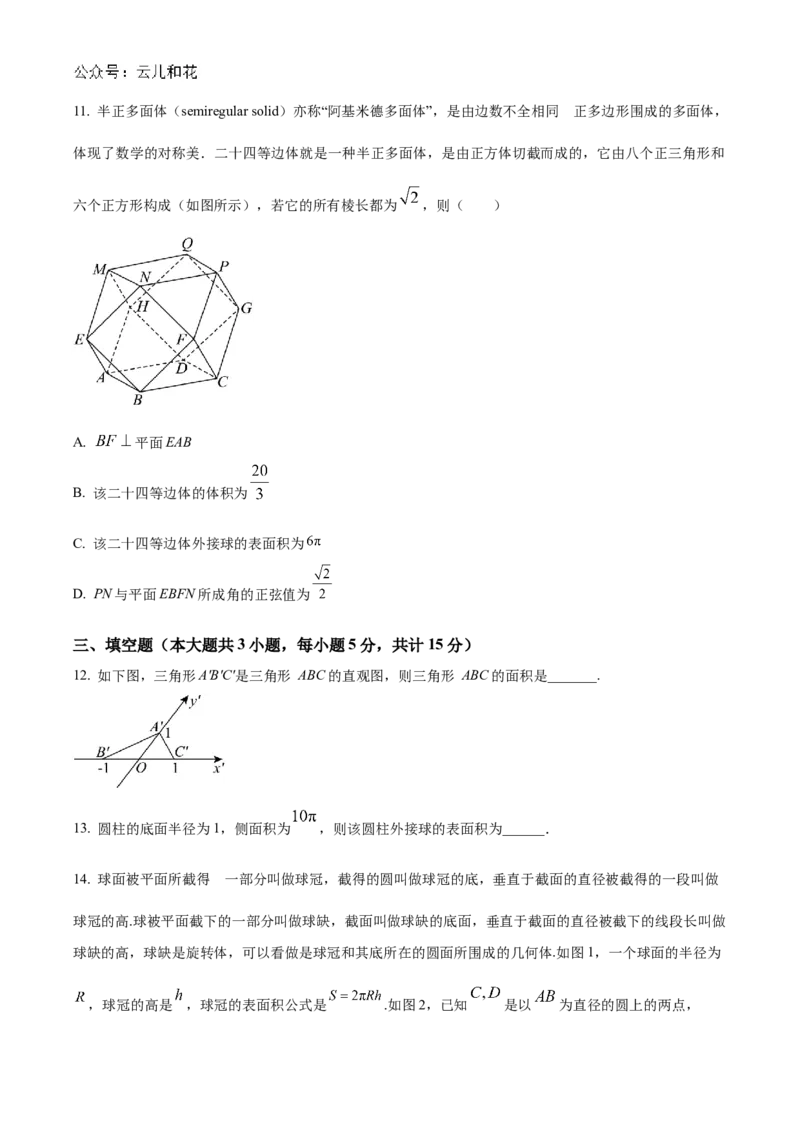
11. 半正多面体(semiregular solid)亦称“阿基米德多面体”,是由边数不全相同 正多边形围成的多面体,
体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和
六个正方形构成(如图所示),若它的所有棱长都为 ,则( )
A. 平面EAB
B. 该二十四等边体的体积为
C. 该二十四等边体外接球的表面积为
D. PN与平面EBFN所成角的正弦值为
三、填空题(本大题共3小题,每小题5分,共计15分)
12. 如下图,三角形A'B'C'是三角形 ABC的直观图,则三角形 ABC的面积是_______.
13. 圆柱的底面半径为1,侧面积为 ,则该圆柱外接球的表面积为______.
的
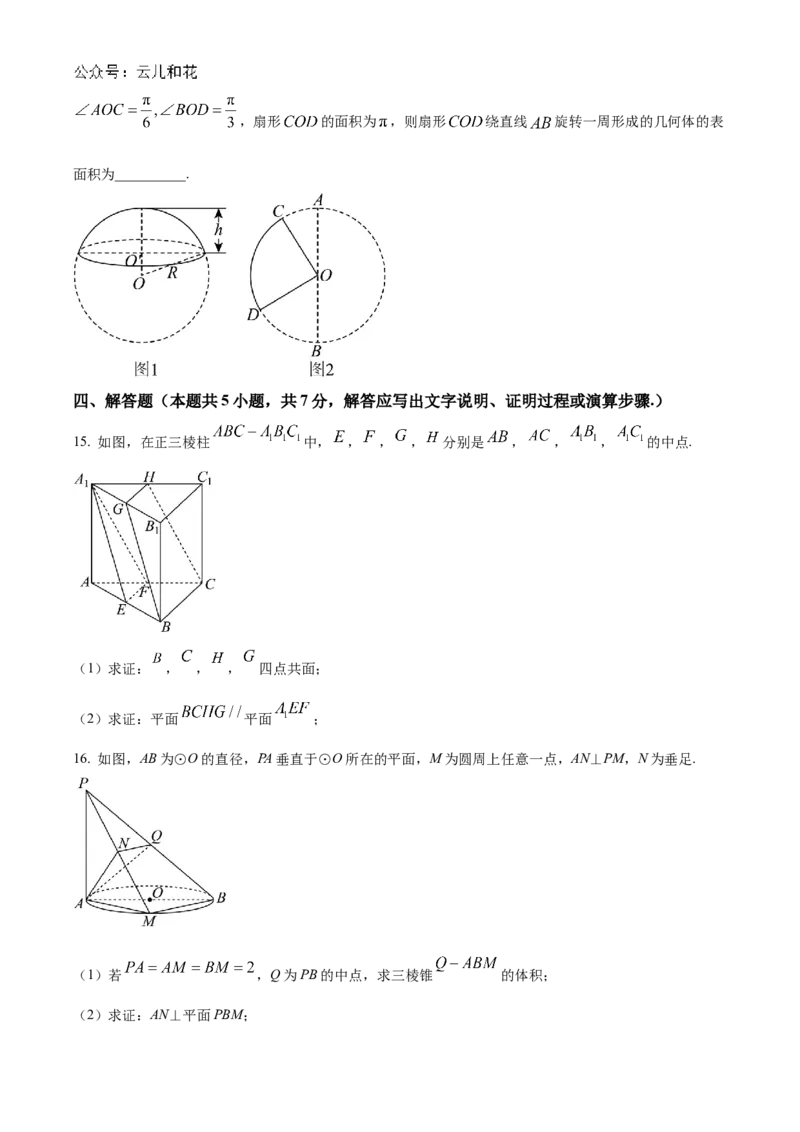
14. 球面被平面所截得 一部分叫做球冠,截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做
球冠的高.球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做
球缺的高,球缺是旋转体,可以看做是球冠和其底所在的圆面所围成的几何体.如图1,一个球面的半径为
,球冠的高是 ,球冠的表面积公式是 .如图2,已知 是以 为直径的圆上的两点,,扇形 的面积为 ,则扇形 绕直线 旋转一周形成的几何体的表
面积为__________.
四、解答题(本题共5小题,共7分,解答应写出文字说明、证明过程或演算步骤.)
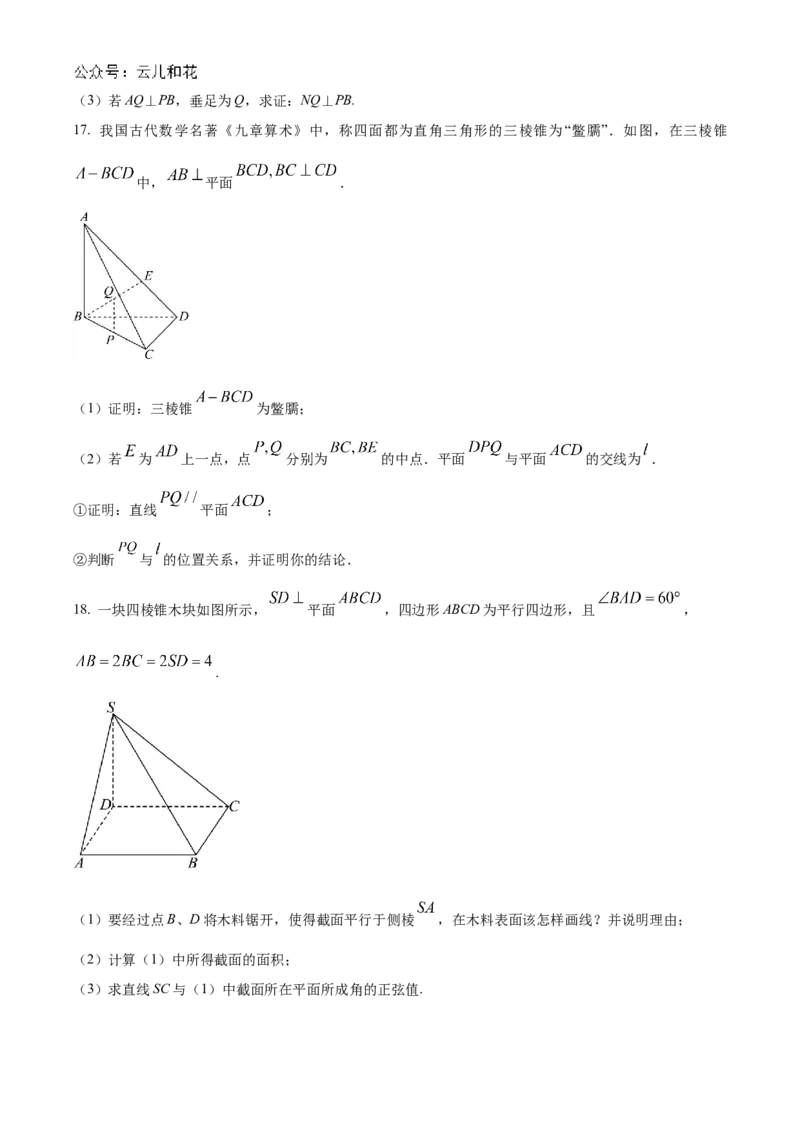
15. 如图,在正三棱柱 中, , , , 分别是 , , , 的中点.
(1)求证: , , , 四点共面;
(2)求证:平面 平面 ;
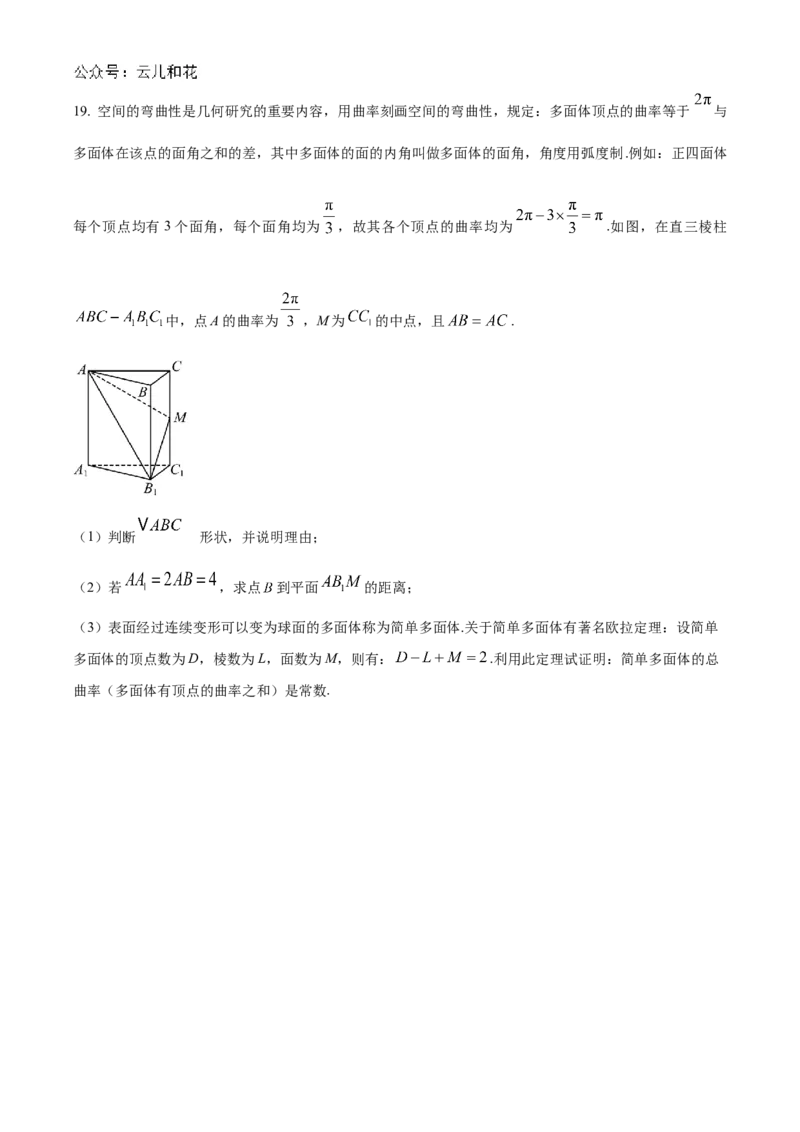
16. 如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.
(1)若 ,Q为PB的中点,求三棱锥 的体积;
(2)求证:AN⊥平面PBM;(3)若AQ⊥PB,垂足为Q,求证:NQ⊥PB.
17. 我国古代数学名著《九章算术》中,称四面都为直角三角形的三棱锥为“鳖臑”.如图,在三棱锥
中, 平面 .
(1)证明:三棱锥 为鳖臑;
(2)若 为 上一点,点 分别为 的中点.平面 与平面 的交线为 .
①证明:直线 平面 ;
②判断 与 的位置关系,并证明你的结论.
18. 一块四棱锥木块如图所示, 平面 ,四边形ABCD为平行四边形,且 ,
.
(1)要经过点B、D将木料锯开,使得截面平行于侧棱 ,在木料表面该怎样画线?并说明理由;
(2)计算(1)中所得截面的面积;
(3)求直线SC与(1)中截面所在平面所成角的正弦值.19. 空间的弯曲性是几何研究的重要内容,用曲率刻画空间的弯曲性,规定:多面体顶点的曲率等于 与
多面体在该点的面角之和的差,其中多面体的面的内角叫做多面体的面角,角度用弧度制.例如:正四面体
每个顶点均有3个面角,每个面角均为 ,故其各个顶点的曲率均为 .如图,在直三棱柱
中,点A的曲率为 ,M为 的中点,且 .
的
(1)判断 形状,并说明理由;
(2)若 ,求点 到平面 的距离;
(3)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单
多面体的顶点数为D,棱数为L,面数为M,则有: .利用此定理试证明:简单多面体的总
曲率(多面体有顶点的曲率之和)是常数.2024-2025 学年高二第一学期第一次月考数学科试题
一、单选题(本大题共8小题,每小题5分,共40分.每小题给出的四个选项中,只有一个选
项是正确的.请把正确的选项填涂在答题卡相应的位置上.)
【1题答案】
【答案】B
【2题答案】
【答案】A
【3题答案】
【答案】C
【4题答案】
【答案】D
【5题答案】
【答案】D
【6题答案】
【答案】A
【7题答案】
【答案】C
【8题答案】
【答案】C
二、多选题(本大题共3小题,每小题6分,共计18分.每小题给出的四个选项中,有多项符
合题目要求.全部选对得6分,选对但不全的部分分,有选错的得0分.)
【9题答案】
【答案】BC
【10题答案】
【答案】ABD
【11题答案】
【答案】BD
三、填空题(本大题共3小题,每小题5分,共计15分)
【12题答案】
【答案】2
【13题答案】【答案】
【14题答案】
【答案】
四、解答题(本题共5小题,共7分,解答应写出文字说明、证明过程或演算步骤.)
【15题答案】
【答案】(1)证明见解析
(2)证明见解析
【16题答案】
【答案】(1)
(2)证明见解析 (3)证明见解析
【17题答案】
【答案】(1)证明见解析;
(2)①证明见解析;②平行,证明见解析.
【18题答案】
【答案】(1) 即为要画的线,理由见解析;
(2)
(3)
【19题答案】
【答案】(1) 为等边三角形,理由见解析
(2)
(3)证明见解析