四川省名校联盟2025届高三12月联考数学_2024-2025高三（6-6月题库）_2024年12月试卷_1218四川省名校联盟2025届高三12月联考试卷（全科）

2024年12月 四川省名校联盟高 2 0 2 2 级 12 月联考 数学试卷 一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.) 1.已知z(1−3i)=10，则 1 z = ( ) A.2−3i B.1+3i C.3i D.−3i 2.已知单位向量 a , b 满足 a + b = a − b ，则 a+2b =( ) A. 8 B. 3 C.2 2 D. 5 3.已知命题 p：xR,ex +e−x 2，命题q:x ( 0,10 ) ， x(10−x) 5，则( ) p A.命题 与 q 均为真命题 B.命题 p 与  q 均为真命题 p C.命题 与 q 均为真命题 D.命题  p 与  q 均为真命题 4.已知平行四边形 A B C D 的顶点 A ( 0 , 1 ) ，边AB所在直线方程是 x − y + 1 = 0 ，对角线的交点为 M ( 2 , 2 ) ， 则边 C D 所在直线方程为( ) A. x − y − 1 = 0 B. x − y + 2 = 0 C. x + y − 1 = 0 D. x + y − 3 = 0 5.设 m , n 为两条不同的直线， , , 是三个不同的平面，则下列说法一定成立的是( ) A.若   ∥ ， m ∥ ，则  m ∥ B.若⊥，⊥，则  ∥ C.若   m ∥ n ， m ⊥ ， n ⊥ ，则∥ D.若 m ， n 与所成角相等，则m∥n 6.点 P 在边长为1的正三角形 A B C 的外接圆上，则 A P  A B 的最大值为( ) A. 3 3 + 1 2 B. 3 2 + 1 2 3 3 C. D. 3 2 7.已知实数 a 满足2a +a =2，则函数 f(x)=2x3−3x2 +1−a的零点个数为( ) A. 0 B.1 C.2 D. 3 8.已知函数 f(x)=ln(x2 −2x+3)+e|x−1|，设a= f(0)， b = f ( l o g 3 4 ) ，c= f(log 5)，则a， 4 b ， c 的 大小关系是( ) A.abc B.bac C.cba D.bca二、多选题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的 得6分,部分选对的得部分分,有选错的得0分.) 9.为了研究某校高三年级学生的性别和身高是否低于170cm的关联性，研究小组从该校高三学生中获取容 量为500的有放回简单随机样本，由样本数据整理得到如下列联表： 单位：人 附： 2 2 = ( a b ) n ( c ( a d d ) ( b a c + ) c 2 ) ( b d )  + + − + ，其中 n = a + b + c + d .  0.1 0.05 0.01 x 2.706 3.841 6.635  小组成员甲用该列联表中的数据进行独立性检验，小组成员乙将该列联表中的所有数据都缩小为原来的 1 1 0 后再进行独立性检验，则下列说法正确的是( ) A.依据=0.01的独立性检验，小组成员甲可以认为该中学高三年级学生的性别与身高有关联 B.依据=0.01的独立性检验，小组成员甲不能认为该中学高三年级学生的性别与身高有关联 C.小组成员甲、乙计算出的 2  值相同，依据=0.01的独立性检验，他们得出的结论也相同 D.小组成员甲、乙计算出的 2  值不同，依据 = 0 . 0 1  的独立性检验，他们得出的结论也不同 10.已知数列 { a n } ( n    ) 为无穷等差数列，公差为d ，前 n 项和为 S n ，则下列说法正确的是( ) A.若 S 5 = S 1 7 ， d ＜ 0 ，则a 0，a 0 11 12 B.若m,n,p,q且互不相等，则 a m m − − a n n = a p p − − a q q C.若m,n,p,q， m ＜ p ＜ n ＜ q ， m + n = p + q ，则 a m a n  a p a q D.若 a 2 0 2 5 = 0 ，则 a 1 + a 2 + . . . + a n = a 1 + a 2 + . . . + a 4 0 4 9 − n ( n   ， n  4 0 4 9 ) 11.已知函数 f (x)=sinn x+cosn x，n，则下列说法正确的是( ) n 3 A.若cos2x= ，则 5 f 4 ( x ) = 1 2 7 5   B.当x[− , ]时，函数 2 2 y = f 4 ( x ) 身高 性别 低于 不低于 合计 170cm 170cm 女 140 60 200 男 120 180 300 合计 260 240 500 3 与y=sin4x+ 的图象恰有5个交点 4  C.当n=2k+1,k*时，函数y = f (x)的图象关于直线x= 成轴对称图形 n 4 n D.当n=2k,k*时，记函数 f (x)的最小值为a ，则 a 2 2k k k k=1三、填空题(本题共3小题,每小题5分,共15分.把答案填在题中的横线上.) 12.已知椭圆 3 C 的中心为坐标原点，焦点在 x 轴上，且经过点 P ( 2 , 0 ) ， Q ( 0 , 1 ) ，则椭圆 C 的标准方程为 _______. 13.已知棱长为1的正四面体 P − A B C ， E ， F 分别为 P A ， B C 的中点，若以 E F 的中点 O 为球心的球 与该正四面体的棱有公共点，则球 O 半径的最大值为_______. 14.整数的商 m n (其中 n  0 m )称为有理数，任一有限小数或无限循环小数可以化为整数的商 (其中 n n  0 ) 的形式，则 1 . •2 = _______(写成 m n 的形式，m与 n 为互质的具体正整数)；若1.2，1.22，1.222，    构 成数列  a n  1 ，令b = ， n ( 10n+1−1 ) (a −1) n S n 为数列  b n  的前 n 项和，则 S n 的取值范围为_______. 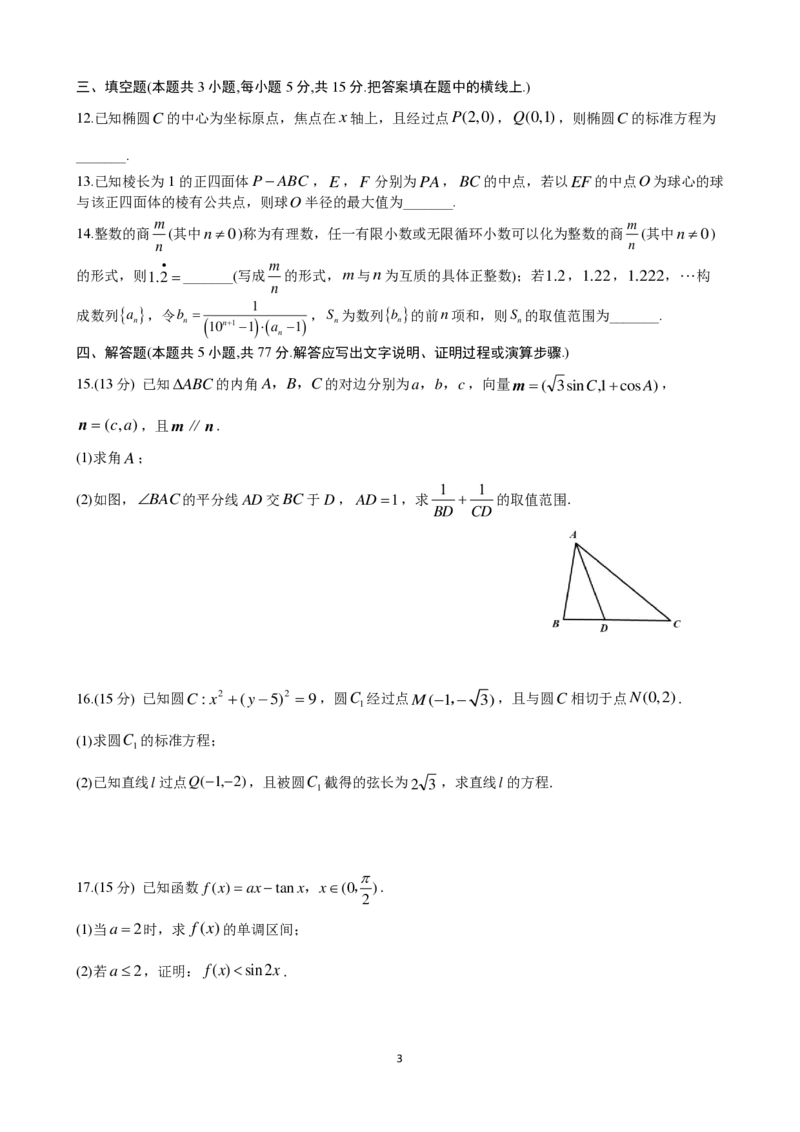四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.) 15.(13分) 已知  A B C 的内角A，B，C的对边分别为 a ， b ， c ，向量 m = ( 3 s in C ,1 + c o s A ) ， n = ( c , a ) ，且 m ∥ n . (1)求角 A ； (2)如图，  B A C 的平分线 A D 交 B C 于 D ，AD=1，求 B 1 D + C 1 D 的取值范围. 16.(15分) 已知圆C:x2 +(y−5)2 =9，圆C 经过点M(−1，− 3)，且与圆C相切于点 1 N ( 0 , 2 ) . (1)求圆 C 1 的标准方程； (2)已知直线l过点 Q ( − 1 , − 2 ) ，且被圆 C 1 截得的弦长为 2 3 ，求直线l的方程. 17.(15分) 已知函数 ( ) t a n ( 0 2 )  f x = a x − x ， x  ， . 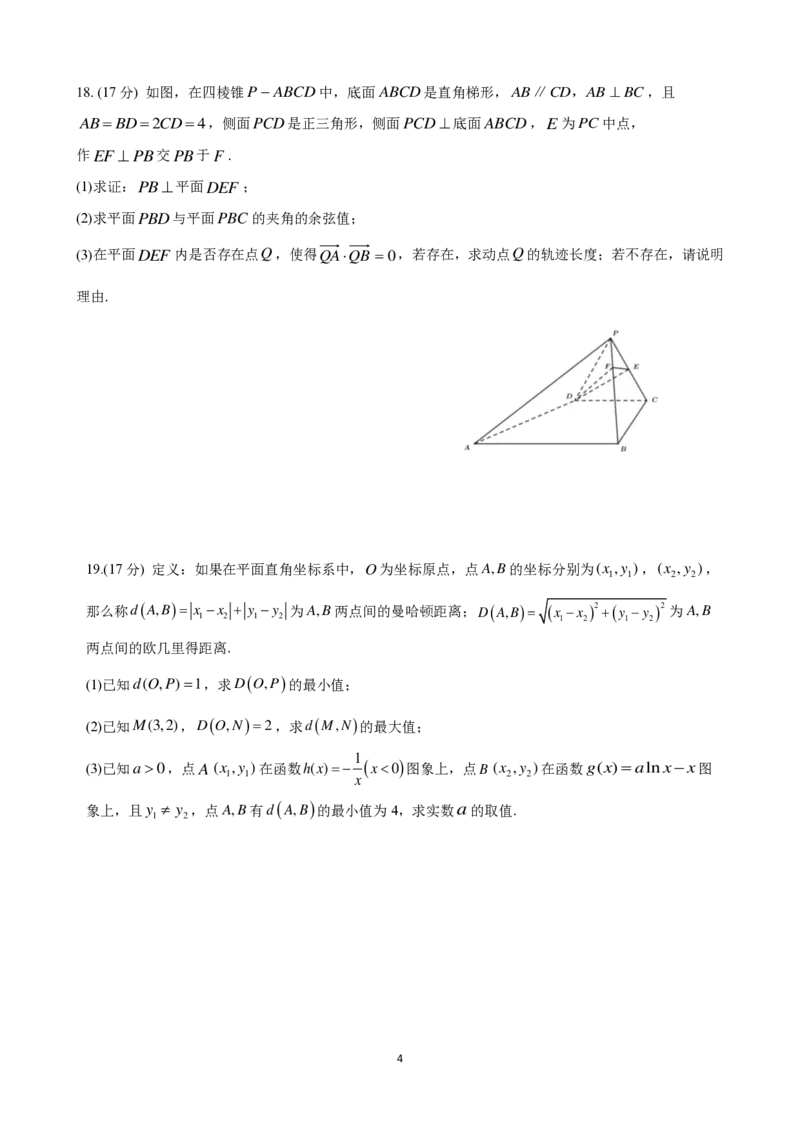(1)当a=2时，求 f ( x ) 的单调区间； (2)若a2，证明： f(x)sin2x.18. (17分) 如图，在四棱锥 4 P − A B C D 中，底面 A B C D 是直角梯形， A B ∥ C D ， A B ⊥ B C ，且 AB=BD=2CD=4，侧面 P C D 是正三角形，侧面 P C D ⊥ 底面ABCD，E为 P C 中点， 作 E F ⊥ P B 交 P B 于 F . (1)求证： P B ⊥ 平面DEF； (2)求平面 P B D 与平面 P B C 的夹角的余弦值； (3)在平面 D E F 内是否存在点 Q ，使得 Q A  Q B = 0 ，若存在，求动点 Q 的轨迹长度；若不存在，请说明 理由. 19.(17分) 定义：如果在平面直角坐标系中， O 为坐标原点，点A,B的坐标分别为 ( x 1 , y 1 ) ， ( x 2 , y 2 ) ， 那么称d(A,B)= x −x + y −y 为 1 2 1 2 A , B 两点间的曼哈顿距离； D ( A , B ) = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 为 A , B 两点间的欧几里得距离. (1)已知 d ( O , P ) = 1 ，求 D ( O , P ) 的最小值； (2)已知M(3,2)， D ( O , N ) = 2 ，求 d ( M , N ) 的最大值； (3)已知 a  0 ，点A ( x 1 , y 1 ) 在函数 h ( x ) = − 1 x ( x  0 ) 图象上，点B (x ,y )在函数 2 2 g ( x ) = a l n x − x 图 象上，且 y 1  y 2 ，点A,B有 d ( A , B ) 的最小值为4，求实数a的取值.